Solmun tehtäviä
Tehtävät sopivat lukiolaisten lisäksi myös edistyneille yläkoululaisille.
1. Ratkaise yhtälö
\[\sqrt{7+\frac{3}{\sqrt{x}}}=7-\frac{9}{x},\]
kun \(x\) on reaaliluku.
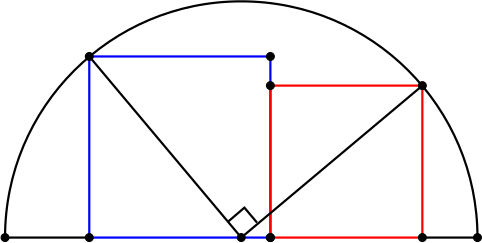
2. Yksikköpuoliympyrän (eli puoliympyrän, jonka säde on 1) sisään piirretään kaksi neliötä siten, että molempien neliöiden yksi sivu on puoliympyrän halkaisijalla ja yksi kärki on puoliympyrällä sekä yksi kummankin neliön sivuista sijaitsee samalla suoralla (katso alla oleva kuva). Ympyrän keskipisteestä neliöiden puoliympyrällä sijaitseviin kärkiin piirrettyjen janojen välinen kulma on suora. Osoita, että näin piirrettyjen neliöiden pinta-alojen summa on aina sama.
3. Ravintolassa tarjottava keitto osoittautui liian suolaiseksi. Kokki päätti laimentaa keittoa edellisenä päivänä yli jääneellä keitolla, jossa ei ollut tarpeeksi suolaa. Suolaisen keiton suolapitoisuus on 5 prosenttia ja edellisen päivän keiton suolapitoisuus on 1,2 prosenttia. Kuinka paljon kumpaakin keittoa tulee lisätä, jotta sekoitettua keittoa saadaan 72 desilitraa ja sen suolapitoisuus on 3,48 prosenttia?
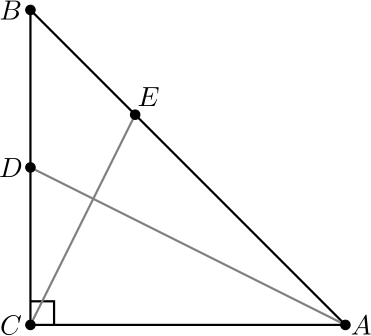
4. Suorakulmaisessa tasakylkisessä kolmiossa \(ABC\) kateetin \(BC\) keskipiste on \(D\) ja hypotenuusalla \(AB\) lähempänä kärkeä \(B\) oleva piste \(E\) jakaa hypotenuusan suhteessa \(1:2\). Osoita, että janat \(AD\) ja \(CE\) ovat kohtisuorassa toisiaan vastaan.
5. Tarkastellaan funktioita \[f_0(x)=\frac{1}{1-x}\quad\text{ja}\quad f_n(x)=f_0(f_{n-1}(x)),\] kun \(n\) on positiivinen kokonaisluku. Laske \(f_{2023}(2023)\).
6. Merkintä \(\lfloor x\rfloor\) tarkoittaa lattiafunktiota reaaliluvusta \(x\), jonka arvo on suurin kokonaisluku, joka ei ole suurempi kuin \(x\), siis
\[\lfloor x\rfloor=\max\{n\in\mathbb{Z}\mid n\le x\}.\]
Esimerkiksi \(\lfloor 2{,}5\rfloor=2\), \(\lfloor -0{,}2\rfloor=-1\) ja \(\lfloor 10\rfloor=10\).
Tarkastellaan funktioita
\[\begin{align*} f(x)&=\sqrt{x+5},\\[2pt] g(x)&=\frac{-2x+8}{5},\\[2pt] h(x)&=\lfloor x+3\rfloor. \end{align*}\]
Määritä funktioiden kuvaajien yhteiset pisteet.
7. Olkoot \(a>2\), \(b\) ja \(c\) reaalilukuja. Tarkastellaan seuraavia kolmea väittämää.
Yhtälöllä \(ax^2+bx+c=0\) ei ole reaalisia ratkaisuja.
Yhtälöllä \((a-1)x^2+(b-1)x+(c-1)=0\) on yksi reaalinen ratkaisu.
Yhtälöllä \((a-2)x^2+(b-2)x+(c-2)=0\) on kaksi reaalista ratkaisua.
(a) Jos väittämät (1) ja (2) ovat totta, niin onko myös väittämä (3) totta?
(b) Jos väittämät (2) ja (3) ovat totta, niin onko myös väittämä (1) totta?
8. Onko totta, että jos kolmion jokaisen kulman sini on rationaalinen, niin myös jokaisen kulman kosini on rationaalinen?
9. Osoita, että jos \(0<a,b<1\), niin
\[(a+b-ab)(a^b+b^a)>a+b.\]
10. \(5\times 5\)-ruudukko täytetään satunnaisessa järjestyksessä kirjoittamalla jokaiseen ruutuun luku. Ruutuun kirjoitettava luku määräytyy sen mukaan, kuinka moni vieressä olevassa ruutu on jo täytetty. Vierekkäin olevia ruutuja ovat ne, joilla on yhteinen sivu. Esimerkiksi alla oleva ruudukko on täytetty luvuilla seuraavassa järjestyksessä: a5, b5, c5, d5, e5, e4, e3, e2, a4, a3, a2, a1, b1, c1, d1, e1, b4, c4, b3, b2, c2, d2, d3, d4, c3.
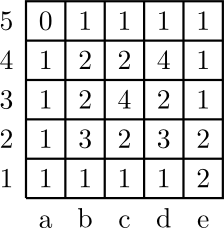
Täytä ruudukko kahdella muulla tavalla säääntöjä noudattaen. Osoita, että ruudukkoon täytettyjen lukujen summa on aina 40 riippumatta siitä, missä järjestyksessä ruudukko on sääntöjä noudattaen täytetty.
Tehtävien ratkaisut julkaistaan Solmun seuraavassa numerossa.
Lähde: KöMaL
Käännös ja sovitus suomeksi: Mika Koskenoja