Vertailevaa geometrian opetusta
Hannu Korhonen
Koulugeometria on valtaosin nimeämistä ja laskemista. Monet tasogeometrian perustulokset ovat liian itsestäänselvän tuntuisia ollakseen todella kiinnostavia. Vertaileminen pallon pinnan geometriaan saattaisi antaa oppimiseen syvyyttä sekä uusia näkökulmia ja virikkeitä ajatteluun.
Ajattelua avartamaan
Vielä kuutisenkymmentä vuotta sitten geometria oli koulussa omana oppiaineenaan. Se jäi algebran ja analyysin jalkoihin, kun peruskouluun tultaessa muodostettiin yhteinen oppiaine nimeltään matematiikka (Coxeter & Gretzer, 1967; Silfverberg, 1999, 17–18). Nykyäänkin kuvioita kyllä tunnistetaan, nimetään ja luokitellaan, mutta varsinainen geometrinen ajattelu hahmottamisen, tarkan piirtämisen, tutkimisen ja todistamisen mielessä jäävät vähälle. Usein siirrytäänkin aivan liian nopeasti kaavojen opetteluun sekä pituuksien ja pinta-alojen laskemiseen (Sarenius, 2010).
Tavanomaisen eli euklidisen tasogeometrian kuvioiden perusominaisuudet tuntuvat monesti myös niin ilmeisiltä ja yksinkertaisilta, että ne eivät innosta eivätkä tunnu antavan aihetta syvempään pohdiskeluun. Kolmion kulmasumma on aina sama \(180^{\circ}\). Suoran ulkopuolella olevan pisteen kautta kulkee aina tasan yksi annetun suoran suuntainen suora. Suorakulmaisen kolmion sivuille piirretään aina vain neliöt ja niiden pinta-aloja koskevaa Pythagoraan lausetta käytetään yksinomaan laskemiseen.
Jo pienikin tavanomaisen asian tekeminen uudella tavalla saattaisi tuoda uutta innostusta, kiinnostusta tai ainakin uutuudenviehätystä. Neliön kallistaminen suunnikkaaksi geolaudalla sisältää samat ajattelun vaiheet kuin kuvasarjan piirtäminen ruutuvihkoon, mutta kumilenkki tekee kuviosta dynaamisen ja konkreettisen.
Toinen, erilainen kokemus samasta asiasta voisi olla sähköisen työvälineen, esimerkiksi Geogebran, käyttäminen. Ohjelma saadaan jopa näyttämään kuvion pinta-ala automaattisesti, jolloin huomio voidaan kohdistaa vain kuvion muodon muuttamiseen ja varsinainen havainto tulee ilman ruuduittain laskemista (Korhonen, 2018).

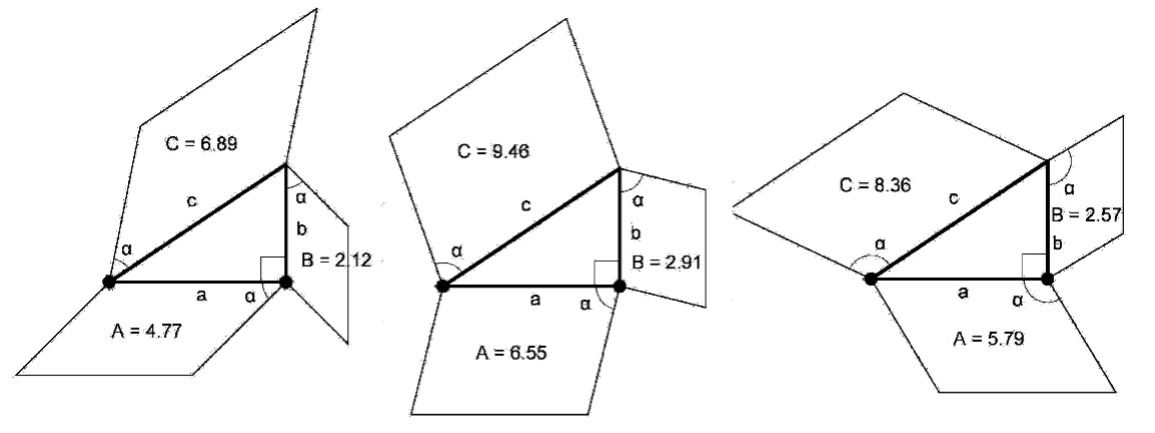
Monia tilanteita voidaan myös ajatella ihan uudestaan tai ainakin tavanomaista laajemmin entä jos -kysymyksen avulla. Entä jos suorakulmaisen kolmion sivuille piirretäänkin jotkin muut yhdenmuotoiset kuviot kuin neliöt (Korhonen, 2021)? Onko kateeteille piirrettyjen kuvioiden pinta-alojen summa silloinkin yhtä suuri kuin hypotenuusalle piirretyn kuvion ala? Ei enää Pythagoraan lause, vaan jonkinlainen yleistys.
Vertailevaa geometriaa
Pahimmillaan – tai parhaimmillaan – entä jos -kysymys saattaa johtaa ulos tutusta ja turvallisesta koulugeometriasta ja tehdä geometriasta yllättävää, kiinnostavaa, jopa hauskaa. Entä jos suoran ulkopuolella olevan pisteen kautta ei voitaisi piirtää yhtään suoran kanssa yhdensuuntaista suoraa? Onko sellaista tilannetta vaikeaa kuvitella? Tuntuuko siltä, että ainahan yhdensuuntaisen voi piirtää? Matematiikka voi kyllä tehdä mahdollisesta mahdotonta. Pitää vain valita geometria, jossa yhdensuuntaisia ei ole.
Apua saadaan Unkarista. Vertailevan geometrian opetuksen menetelmässään István Lénárt on esittänyt tasogeometrian vertaamista pallon pinnan geometriaan (Lénárt, 1995). Siihen tarkoitukseen hän on suunnitellut opetusvälineen: Lénártin pallon. Se on kaksikymmensenttinen läpinäkyvä muovipallo, jonka pintaan voi piirtää kuvioita tussikynällä. Lisävarusteina on pöytäteline, palloharppi, isoympyräviivain, tussikyniä sekä maapallokarttapohja (Korhonen, 2004).
Ennen kuin ryhdymme vertailemaan taso- ja pallogeometriaa, on tarpeen pohtia, mitä ominaisuuksia tavallisella tasolla on. Siinä on esimerkiksi mahdollista liikkua vain kahteen suuntaan: eteen-taakse ja oikealle-vasemmalle. Kolmatta suuntaa ylös-alas tasossa ei ole, vaikka tavallisessa kolmiulotteisessa ympäristössämme onkin. Taso on siis vain kaksiulotteinen. Kaksiulotteisuus on itse asiassa kaikkien pintojen ominaisuus, siis myös pallon pinnan. Se eroaa tasosta siinä, että se on kaareva, mutta on siis pintana vain kaksiulotteinen niin kuin tasokin.

Taso- ja pallopinta ovat samanlaisia myös siinä, että niitä pitkin voi kulkea ilman, että mitään rajaa tulee vastaan. Erona taas on se, että tasolla eteneminen vie aina vain yhä kauemmas, mitä kuvataan sanomalla tason jatkuvan äärettömyyteen. Pallopinnalla kulkija palaa takaisin lähtöpaikkaansa kuljettuaan pallon ympäri. Hänen maailmansa on äärellinen, sillä hän ei voi päästä kauas, vaikka mitään rajaa ei tulekaan vastaan.
Pallogeometrian perusideat
Kaarevuuden takia pallon pinnalla ei voi olla janoja eikä suoria. Sen geometria on siis sovittava uudella tavalla. Luontevin tapa lähestyä sitä on tutkia, miten mitataan pallon pinnan kahden pisteen lyhin etäisyys. Tavallinen geometrian käsityksemme saa ajattelemaan, että lyhin etäisyys olisi näiden pisteiden yhdistysjanan pituus.
Tämä määrittely ei kuitenkaan sovi pallon pinnan geometrian pohjaksi, sillä yhdistysjana ei ole pallon pinnalla, vaan kulkee pallon sisällä. Kun halutaan rakentaa pinnan geometriaa, niin lyhimmän etäisyyden määrittelevän viivan on kuljettava pinnalla. Sitä pitkin etäisyys sitten mitataan.
Tässä jutussa tarkastelen asiaa vain perushahmotuksen kannalta pyrkimättäkään varsinaisen pallogeometrian opettamisen kysymyksiin. Käsittely vastaa siis lähinnä van Hielen määrittelemiä geometrisen ajattelun tasoja 1 ja 2 (Silfverberg 1999, 27, 29).
Lyhimmän etäisyyden viivan saat selville konkreettisimmin, kun otat styrox-pallon, merkitset sen pinnalle kaksi pistettä esimerkiksi nuppineuloilla ja virität kuminauhan nuppineulojen väliin. Se asettuu lyhimmän etäisyyden viivalle. Se on pallon pintaa pitkin kulkeva kaari. Tällainen kaari on aina pallon keskipisteen kautta kulkevassa tasossa.
Tämän kaaren voit kuvitella syntyvän niin, että annettujen pisteiden ja pallon keskipisteen kautta kulkeva taso leikkaa pallon pintaa. Leikkausviiva on ympyrä. Pisteet jakavat sen kahteen osaan. Näistä lyhyempi on pisteiden etäisyys pallon pinnan geometriassa. Kutsutaan sitä pisteiden palloetäisyydeksi ja ympyrää isoympyräksi, koska se on suurin ympyrä, joka voidaan piirtää pallon pinnalle. Pallokartalla päiväntasaaja ja napojen kautta kulkevat pituuspiirit ovat tällaisia. Kannattaa ehkä huomata myös, että yksi piste ei jaa isoympyrää kahdeksi osaksi niin kuin tapahtuu suoralle tasogeometriassa.
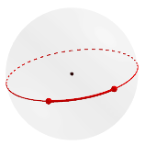
Tasossa kahden pisteen lyhin etäisyys on pisteiden yhdistysjanan pituus. Se on osa pisteiden määrittämästä suorasta. Isoympyrän kaari on vastaavasti pallon pinnalla olevien kahden pisteen välinen lyhin etäisyys. Näin ollen isoympyrällä on pallon pinnalla sama merkitys kuin suoralla on tasossa. Pallon pinnalla ei ole suoria. Siellä niitä vastaavat isoympyrät, lyhimmän etäisyyden määrittelevät viivat.
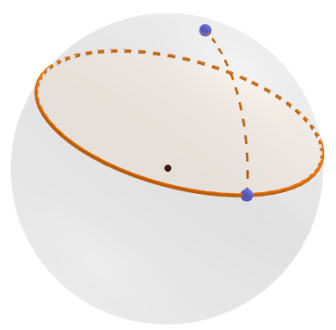
Pallon pinnalle voidaan tietysti piirtää muitakin ympyröitä kuin isoympyröitä. Määritelmä on luonnollisesti sama kuin tasogeometriassa: niiden pisteiden joukko, jotka ovat samalla etäisyydellä annetusta keskipisteestä. Etäisyys mitataan nyt vain pallon pintaa pitkin, joten ympyrän pallosäde on pallon pinnalla olevan keskipisteen kautta kulkevan, ympyrää vastaan kohtisuoran isoympyrän kaari.
Pallokaksikulmio ja -kolmio
Pallomonikulmioiksi voidaan kutsua kuvioita, joita rajoittavat isoympyrät. Tasossa kaksi suoraa eivät voi rajata suljettua kuviota, mutta pallon pinnalla kaksi isoympyrää tekevät aina niin, sillä mitkä tahansa kaksi isoympyrää leikkaavat toisensa tasan kahdessa pisteessä. Leikkauspisteet ovat pallon vastakkaisilla puolilla niin kuin maapallon pohjois- ja etelänapa.
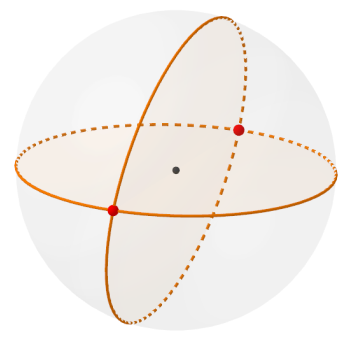
Kaksi isoympyrää jakavat pallon pinnan itse asiassa neljään osaan. Leikkauspisteet ovat kaikkien osien yhteisinä kärkipisteinä. Vastakkaiset osat ovat yhtä suuria. Osan reunoina ovat isoympyröiden puolikkaat. Kuviolla on vain kaksi kärkipistettä. Siksi sen nimi voisi olla pallokaksikulmio. Sen kulmat ovat yhtä suuret. Kuvio on siis säännöllinen. Kärkikulma on sama kuin isoympyrät määrittelevien tasojen välinen kulma. Se voi vaihdella välillä 0–\(180^{\circ}\). Pallokaksikulmion pinta-ala on siten suurimmillaankin enintään puolet pallon pinta-alasta.
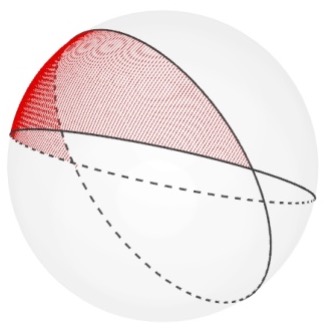
Pallokolmiolla on kolme kärkipistettä ja kolme sivua samoin kuin tasokolmiolla. Sivut ovat nyt vain isoympyränkaaria, kun tasokolmion sivut ovat janoja. Ensikatsannolla ei ole ehkä helppoa huomata, että nämä kaaret jakavat pallon pinnan kahdeksi pallokolmioksi.
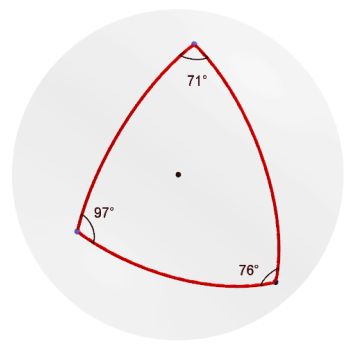
Tämä käy ilmeiseksi, jos kolmiosi on viritetty kumilenkillä styrox-pallolle pistettyjen nuppineulojen varaan. Merkitse kolmion sisään piste ja ryhdy siirtämään kärkipisteitä yhä kauemmaksi merkitsemästäsi pisteestä. Kun kärkipisteet ovat tarpeeksi kaukana pallon toisella puolella, niin huomaat, että se osa pallon pinnasta, joka aikaisemmin näytti vain kolmion ulkopuolelta, alkaa hahmottua yhä paremmin kolmioksi, ja alkuperäinen kolmio näyttääkin nyt sen ulkopuolelta. Kumpikin ovat kuitenkin edelleen kolmen kärkipisteen määrittämien isoympyränkaarien rajoittamia alueita ja siten edelleen pallokolmioita.

Pallokolmiota rajoittavat kolme isoympyrää jakavat pallon pinnan kaikkiaan kahdeksaksi pallokolmioksi. Mitä voit päätellä muiden kolmioiden kulmien suuruudesta yhden kolmion kulmien perusteella? – Suuremman yllätyksen tarjoavat yhden kolmion kulmat. Kulmien summa ei olekaan vakio! Jonkinlaista viitettä pallokolmion kulmien summan muuttumisesta saat jäljempänä olevasta kuvasarjasta (kuva 4). Tarkempaan tutkimiseen tarvitsisit oikeastaan dynaamisen mallin, joka mittaa kulmat valmiiksi (esimerkiksi Korhonen, 2019a). Ohjeita tutkimiseen on myös Dimensio-lehdessä (Korhonen, 2019b).

Kaarevuuden vaikutus
Palloneliö on samalla tavalla säännöllinen kuvio kuin tasoneliökin. Sen kulmat ovat yhtä suuret ja sivut yhtä pitkät. Sivut vain ovat isoympyrän osia ja kulmat muuttuvat neliön koon mukana samoin kuin pallokolmionkin kulmat. Palloneliön reuna jakaa pallon pinnan itse asiassa kahdeksi palloneliöksi samalla tavalla kuin pallokolmion reuna jakaa pallon pinnan kahdeksi pallokolmioksi. Kuvassa palloneliön kulmien summa on \(400^{\circ}\). Kuinka suuri on toisen palloneliön kulmien summa, sen joka pitää sisällään pallon takapuolenkin?

Jos neliö on hyvin pieni, niin sen kulmat ovat vain vähän yli \(90^{\circ}\). Neliön kasvaessa kulmatkin kasvavat. Kun kukin kulma on \(180^{\circ}\), palloneliön sivut ovat toistensa jatkeina, sen piiri on isoympyrä ja ala puolet pallon pinnan alasta (kuva 5). Kun palloneliön pinta-alaa kasvatetaan, niin osa palloneliöstä alkaa olla pallon takapuolella. Neliön ulkopuolesta tulee pienempi kuin sisäpuolesta. Ulkopuoli alkaa näyttää enemmän palloneliöltä kuin sisäpuoli samalla tavalla kuin pallokolmiosta todettiin edellä. Kun pinta-ala kasvaa edelleen, niin kulmat jatkavat kasvamista, mutta piiri alkaa pienentyä. Kuinka suureksi pallokolmion pinta-ala kasvaa, kun sen ulkopuoli supistuu hyvin pieneksi? Kuinka suuriksi kasvavat kulmat?

Ihan pieni palloneliö näyttää hyvin samanlaiselta kuin tasoneliökin. Sen kulmatkin ovat lähellä yhdeksääkymmentä astetta. Tämä johtuu siitä, että pienellä alueella kaarevuus ei vaikuta paljoakaan, vaan pallon pinta on hyvin lähellä tasoa. Siksi pieni palloneliökään ei eroa paljon tasoneliöstä. Juuri tästä syystä monet ihmiset uskoivat vanhaan aikaan, että maa on litteä, kun oma lähiympäristö siltä näytti. Maapallon kaarevuuden voi huomata aavan meren rannalla, kun muutaman kilometrin päässä oleva laiva alkaa kadota taivaanrannan taakse (Youtube, 2016).
Pinta-ala
Tasossa pinta-alan yksikkönä on yksikköneliö, siis neliö jonka sivu on 1 (mm, cm, m tai km kuvion koosta riippuen). Tämä perustuu siihen, että tason voi peittää neliöillä niin, että ne eivät mene päällekkäin eikä neliöiden väliin myöskään jää peittämättömiä rakoja.
Pallon pinnalla tämä ei onnistu. Palloneliön kulmat ovat suurempia kuin suora kulma. Siksi niitä ei voi latoa samalla tavalla vierekkäin pallopinnan peitoksi, koska yhden kulmapisteen ympärille ei voida sijoittaa tasan neljää palloneliötä. On siis keksittävä uusi tapa mitata pallokuvion pinta-alaa.
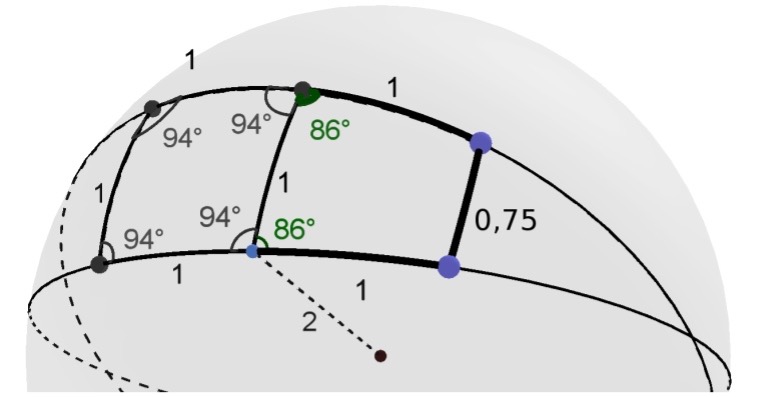
Aloitetaan kolmiosta. Ehkäpä kulmista voisi olla jotain apua, koska kulmat kasvavat kolmion koon mukana. Edellä todettiin myös, että pallokolmion ulkopuolikin on pallokolmio. Pienemmän kolmion kulmien summa näkyy kuvasta. Suuremman kolmion (eli kolmion ulkopuolen) kulmien summa on kolmion kulmien eksplementtikulmien summa.
Jos esimerkiksi katsotaan kuvan 5 kolmioita oikealta vasemmalle, niin kolmion pienentyessä kulmien summa lähestyy 180 astetta eli siis tasogeometriasta tuttua kolmion kulmasummaa. Isomman kolmion kulmien summa lähestyy lukemaa
\[3 \cdot 360^{\circ} - 180^ {\circ} = 900^{\circ}.\]
Lopulta isompi kolmio täyttää pallon koko pinnan.
Pallon pinta-alaa ei ole totuttu mittaamaan asteissa, mutta muunnos on helposti ymmärrettävissä käyttämällä ympyrää apuna. Ympyrän kehän pituus on \(2\pi r\), yksikköympyrälle \(2\pi\), ja sitä vastaava keskuskulma \(360^{\circ}\). Voidaan siis ajatella, että \(2\pi\) on asteissa ilmaistuna \(360^{\circ}\). Pallon pinta-ala on siis \(4\pi r^3 = 720^{\circ} \cdot r^3\). Jos ajatellaan yksikköpalloa, jossa \(r = 1\), niin saadaan verrattaviksi tulokset ‘kulmien summa \(180^{\circ}\) ja pinta-ala noin 0’, kun pallokolmio on hyvin pieni, sekä ‘kulmien summa \(900^{\circ}\) ja pinta-ala \(720^{\circ}\)’, kun pallokolmio on mahdollisimman suuri.
Tästä ei ole suurikaan loikka ajatella, että pallokolmion pinta-ala ilmoitettaisiin asteissa. Silloin se olisi
\[\text{kulmien summa} - 180^{\circ}.\]
Monikulmio, myös pallomonikulmio, voidaan jakaa \(n - 2\) kolmioksi, joten pallo-\(n\)-monikulmion pinta-ala on vastaavasti
\[\text{kulmien summa} - (n - 2) \cdot 180^{\circ}.\]
Ajatusta voidaan jatkaa pitemmälle ja soveltaa myös käyräviivaisiin kuvioihin, mutta siinä tarvitaan jo uusia käsitteitä ja se menee muutenkin tämän tarkastelun rajojen ulkopuolelle.
Matemaatikot käyttävät tätä tapaa, mutta tekevät päätelmän toisessa järjestyksessä ja ottavat ensin kulman mitaksi reaaliluvun samastamalla yksikköympyrän keskuskulman suuruuden ja sen kehän pituuden, mistä saadaan asteelle lauseke reaalilukuna
\[1^{\circ} = \frac{2\pi}{360} = \frac{\pi}{180}.\]
Reaalilukuna ilmoitettua pallomonikulmion kulmien summaa verrataan sitten kuvion pinta-alaan. Koulukursseissa pallon pinnan kuvioiden pinta-aloja ei käsitellä, mutta kulman suuruuden ilmoittaminen reaalilukuna tulee esille lukion matematiikassa.
Koordinaatistot
Tasossa tavallisin koordinaatisto on suorakulmainen eli euklidinen \(xy\)-koordinaatisto. Siinä pisteen paikka ilmoitetaan etäisyytenä \(y\)-akselista (\(x\)-koordinaatti, abskissa) ja etäisyytenä \(x\)-akselista (\(y\)-koordinaatti, ordinaatta).
Pallon pinnalle voidaan rakentaa vastaavanlainen koordinaatisto kiinnittämällä ensin akselit: kaksi kohtisuoraa isoympyrää, esimerkiksi päiväntasaaja ja nollameridiaani. Nämä vastaavat tasokoordinaatiston akseleita. Pisteen paikka ilmoitetaan antamalla pisteen etäisyys nollameridiaanista ja etäisyys päiväntasaajasta asteissa. Juuri näin tehdään maailmakartalla. Etäisyys nollameridiaanista on maantieteellistä pituutta ja etäisyys päiväntasaajasta maantieteellistä leveyttä.
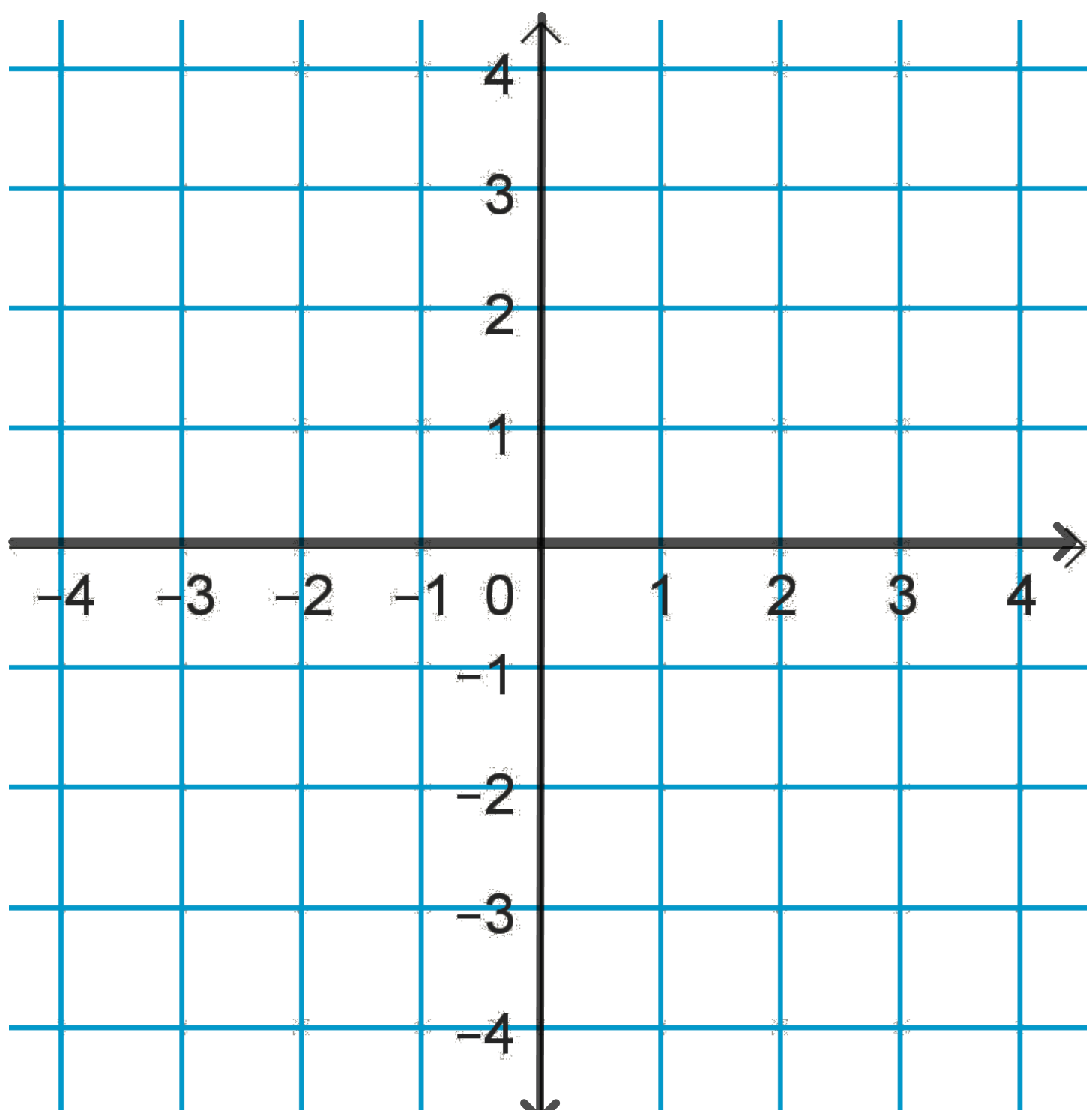

Kuva 7. Taso- ja pallokoordinaatistot.
Tasokoordinaatit voivat olla mitä tahansa reaalilukuja, koska tason ajatellaan jatkuvan rajatta kaikkiin suuntiin. Sen sijaan pallokoordinaatit saavat arvoja vain rajatulta väliltä: \(-180^{\circ} < \text{pituus} \leq 180^{\circ}\) ja \(-90^{\circ} \leq \text{leveys} \leq 90^{\circ}\). Tavallisessa maantieteellisessä puheessa ei käytetä negatiivisia astelukuja, vaan puhutaan itäisestä tai läntisestä pituudesta ja pohjoisesta tai eteläisestä leveydestä. Tarkista oman kotipaikkasi koordinaatit (Luettelo, Wikipedia).
Samantapaista koordinaatistoa käytetään myös taivaalla näkyvien kohteiden suunnan ilmoittamiseen. Maantieteellistä pituutta vastaavaa koordinaattia kutsutaan silloin suuntimaksi (atsimuutti) ja se ilmoitetaan asteina yleensä etelän suunnasta myötäpäivään kiertäen tai esimerkiksi merenkulussa ja suunnistuksessa pohjoisen suunnasta samoin myötäpäivään kiertäen. Se ilmoittaa siis suunnan, jossa kohde näkyy. Maantieteellistä leveyttä vastaa korkeus, joka ilmoitetaan asteissa taivaanrannasta (horisontista) ylöspäin mitattuna. Taivaanlaki on kohtisuoraan katsojasta ylöspäin ja sen korkeus on siten \(90^{\circ}\).
Tähtien paikan ilmoittamiseen käytetään useimmiten katsojasta riippumatonta pallokoordinaatistoa. Sen origo on maapallon keskipisteessä. Koordinaatisto on kiinnitetty maapallon päiväntasaajan tasoon. Maantieteellistä pituutta vastaava koordinaatti on sama kuin edellä. Silloin itäsuunta on siis \(90^{\circ}\) ja etelä \(180^{\circ}\). Korkeus ilmoitetaan nyt päiväntasaajatasosta mitattuna. Taivaannavan suunta on silloin maapallon akselin suunta. Esimerkiksi Pohjantähden korkeus (deklinaatio) on tässä koordinaatistossa \(+89{,}32^{\circ}\), koska se on hyvin lähellä taivaannapaa.
Viitteet
Coxeter, H. S. M. & Greitzer S. L. (1967). Geometry Revisited. The Mathematical Association of America, xi.
Korhonen, H. (2004). Geometriaa pallolla. Dimensio 2 (68). Matemaattis-luonnontieteellinen aikakauslehti, 10–13.
Korhonen, H. (2018). \(N \times n\) -geolauta. Geogebra-materiaali https://www.geogebra.org/m/yxeyt4pw, viitattu 17.3.2019.
Korhonen, H. (2019a). Pallokolmio. Geogebra-materiaali https://www.geogebra.org/m/fcaqrzpr. Viitattu 17.3.2019.
Korhonen, H. (2019b). Pallogeometrian perushahmotusta, osat 1–5. Dimensio, https://www.dimensiolehti.fi/?s=pallogeometria. Viitattu 5.10.2019.
Korhonen, H. (2021). Pythagoraan porsaat. Dimensio, https://dimensiolehti.fi/pythagoraan-porsaat/. Viitattu 20.8.2023.
Lénárt, I. (1995). Non-Euclidean Adventures on the Lenart Sphere: Activities Comparing Planar and Spherical Geometry. Key Curriculum Press.
Luettelo Suomen kuntien koordinaateista. Wikipedia, https://fi.wikipedia.org/wiki/Luettelo_Suomen_kuntien_koordinaateista.
Makara, Á. ja Lénárt I. (2004) Comparative geometry on plane and sphere. Teaching Mathematics and Computer Science, 2/1, 81–101. Saatavissa myös verkosta, viitattu 14.11.2023, https://www.researchgate.net/publication/283835518_Comparative_geometry_on_plane_and_sphere_didactical_impressions.
Sarenius, V-M. (2010) Geometrian opetuksesta. Oulun yliopiston LUMA-keskus. Artikkeli on poistunut verkosta 2023.
Silfverberg, H. (1999) Peruskoulun yläasteen oppilaan geometrinen käsitetieto. Väitöskirja. Acta Electronica Universitatis Tamperensis 6, https://urn.fi/urn:isbn:951-44-4718-2. Viitattu 17.3.2019.
Youtube (2016). Ship over the Horizon. Video, https://www.youtube.com/watch?v=WOZd6t9uzhY. Viitattu 17.3.2019.