Tarinoita polynomeista (osa 3)
Jukka Tuomela
Itä-Suomen yliopisto, Joensuu
jukka.tuomela@uef.fi
Kertaus
Kirjoituksissa [9, 10] katsottiin polynomeja nimenomaan algebran näkökulmasta. Nyt puhutaan siitä, miten polynomit liittyvät geometriaan. Kuten edellisissä kirjoituksissa oletetaan, että lukija tietää mitä tarkoittaa polynomien yhteen- ja kertolasku, ja lisäksi toisen asteen polynomin ratkaisukaava oletetaan tunnetuksi. Tätä ratkaisukaavaa ei kuitenkaan tarvita; muistetaan viime kerralta [10], että juurilausekkeet ja siis ratkaisukaavat eivät oikeastaan ole kovin hyödyllisiä, joten on parempi ja kätevämpi laskea ilman niitä. Parissa kohtaa tulee ratkaistavaksi lineaarinen yhtälöryhmä, ja oletetaan, että lukija osaa ratkaista tämän.
Erinomainen kirja polynomeista kiinnostuneille on [3]. Eukleideen geometriaa modernista näkökulmasta on tarkasteltu Hartshornen kirjassa [5]. Suomeksi Matti Lehtinen on kirjoittanut laajasti Eukleideen geometriasta [7]. wxMaxima, jonka avulla esimerkkejä voi helposti laskea, on vapaasti saatavilla oleva symbolisen laskennan ohjelmisto.1 Myös Sage on ilmainen ohjelmisto, jolla voi laskea sekä symbolisesti että numeerisesti [1].2 Jäljempänä olevat tehtävät voi helposti laskea myös Sagen avulla.
Polynomit ja Eukleideen geometria: käytäntö
Yleensä kilpatehtävissä, ja miksei muutenkin, polynomeihin liittyvät kysymykset pidetään tiukasti erillään geometrian kysymyksistä. Odotetaan, että jos tehtävä on esitetty geometrisesti, niin ratkaisunkin pitäisi olla samaa tyyliä. Kuitenkin monet geometrian tehtävät ratkeavat systemaattisesti polynomien avulla: oikeastaan koko Eukleideen geometria voidaan tulkita polynomien avulla.
Esimerkki 1. Lehtisen tehtäväkokoelmassa Kilpailumatematiikan lajeja ja periaatteita oli seuraava tehtävä.
Kolmion sivujen pituudet ovat \(10\), \(17\) ja \(21\). Määritä kolmion lyhimmän korkeusjanan pituus.
Olkoot kolmion pisteet \(p_0=(0,0)\), \(p_1=(21,0)\) ja \(p_2=(a,b)\). Siis
\[\begin{align*} f_0 &=a^2+b^2-10^2=0,\\ f_1&=(a-21)^2+b^2-17^2=0, \end{align*}\]
ja koska \(f_0-f_1=42a-252=0\), niin \(a=6\), mistä sitten \(b=\pm 8\), joten vastaus on \(8\).3 \(\Box\)
On tapana sanoa, että Eukleideen konstruktiot perustuvat viivottimen ja harpin käyttöön. Mutta viivotin on suora:
\[ax+by+c=0,\]
siis ensimmäisen asteen polynomi, ja harppi on ympyrä:
\[(x-x_0)^2+(y-y_0)^2-r^2=0,\]
siis toisen asteen polynomi. Kaikki konstruktiot voidaan siis esittää (verrattain yksinkertaisten) polynomien avulla.
Luonnollisesti ei aina ole järkevää muuttaa geometrian tehtävää polynomitehtäväksi; monesti geometrinen intuitio johtaa helpompaan ratkaisuun. Tämä näkökulma kuitenkin avaa mahdollisuuden puhtaasti algoritmiseen ratkaisuun. Geometrisessa tehtävässä on joitain oletuksia, ja niistä pitäisi osoittaa jokin väite. Jos edetään systemaattisesti, niin oletukset ovat muotoa
\[f_1=\dots=f_m=0,\]
missä \(f_j\) ovat polynomeja, ja väite on \(h=0\), missä \(h\) on polynomi. Jos väite on totta, niin pitäisi olla olemassa polynomit \(q_j\) siten, että
\[h=q_1f_1+\dots+q_mf_m.\]
Jos siis löydetään tällaiset polynomit, niin tämä todistaa väitteen. Tämän voi ajatella niin, että jaetaan \(h\) polynomeilla \(f_j\), polynomit \(q_j\) ovat osamääriä, ja väite pätee, jos jakojäännös on nolla. Palataan myöhemmin siihen, miten tarkkaan ottaen jaetaan monella polynomilla, ja katsotaan tässä vain esimerkkejä.
Koska tämäntyyppisessä ratkaisussa esiintyy varsin paljon muuttujia/parametreja, niin kannattaa aina valita koordinaatit siten, että lausekkeet ovat mahdollisimman yksinkertaisia. Äskeisessä esimerkissä oli kätevää valita yksi kolmion pisteistä origoksi. Näin voidaan geometrian tehtävissä aina tehdä, koska väitteet eivät riipu pisteitten absoluuttisesta paikasta vaan vain niitten keskinäisistä suhteista. Tämän takia koordinaatistoa voidaan myös kiertää, joten kun on valittu jokin piste \(p=(0,0)\), niin edelleen voidaan valita, että jokin toinen piste on \(q=(a,0)\). Lisäksi usein geometrian tehtävät/väitteet eivät riipu valitusta skaalasta, jolloin voidaan vielä asettaa \(a=1\).

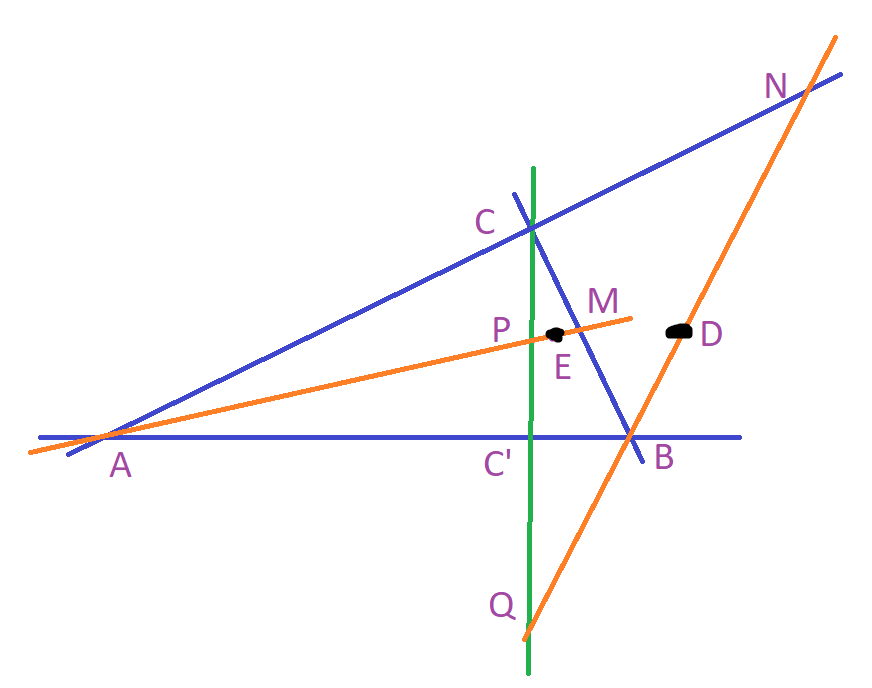
Esimerkki 2. Katsotaan kuvan 1 tilannetta, joka on Lehtisen tehtäväkokoelmassa Kilpailumatematiikan lajeja ja periaatteita. Kulma \(ACB\) on suorakulma, \(BN\) ja \(AM\) ovat kulmanpuolittajia, ja \(D\) on janan \(QN\) keskipiste ja \(E\) on janan \(PM\) keskipiste.
Osoita, että \(DE\) ja \(AB\) ovat yhdensuuntaisia.
Valitaan ensin \(A\) origoksi ja olkoon \(B=(1,0)\). Olkoon edelleen \(D=(x_6,y_6)\) ja \(E=(x_7,y_7)\). Saadaan siis tehtävä
Osoita, että \(h=y_6-y_7=0\).
Olkoon \(kx-y=0\) pisteitten \(A\), \(N\) ja \(C\) kautta kulkeva suora. Koska kulma \(ACB\) on suorakulma, niin heti saadaan, että
\[C=(x_1,y_1)=\left( \frac{1}{k^2+1},\frac{k}{k^2+1}\right).\]
Olkoon edelleen \(C'=(x_1,0)\), \(P=(x_1,y_5)\), \(Q=(x_1,y_4)\), \(N=(x_2,y_2)\) ja \(M=(x_3,y_3)\). Koska \(D\) ja \(E\) puolittavat janat, niin selvästi
\[2h=y_2-y_3+y_4-y_5=kx_2-y_3+y_4-y_5.\]
Huomaa, että \(k\) pitää ajatella vapaasti valittavana parametrina. Pitäisi siis osoittaa, että \(h=0\) kaikilla \(k\):n arvoilla. Välitavoitteena pitäisi nyt laskea \(h\):lle lauseke, jossa esiintyy vain muuttujia \(x_2\) ja \(x_3\) sekä parametri \(k\).
Pisteitten \(B\) ja \(C\) kautta kulkeva suora on \(x+ky-1=0\), joten \(x_3+ky_3-1=0\), mistä saadaan \(y_3\). Edelleen \(x_3y_5-x_1y_3=0\), joten
\[y_5=\frac{1-x_3}{k(k^2+1)x_3}.\]
Suora \(x+cy-1=0\) kulkee pisteen \(N\) kautta, jos \(c=(1-x_2)/(kx_2)\), joten \(y_4\) voidaan ratkaista yhtälöstä \(x_1+cy_4-1=0\), mistä saadaan
\[y_4=\frac{k^3x_2}{(k^2+1)(1-x_2)}.\]
Sijoittamalla nämä \(h\):n lausekkeeseen saadaan
\[\begin{align*} h &=\frac{h_1}{2kx_3(k^2+1)(x_2-1)},\\ h_1 &=x_3(k^2+1)h_0+ k^2x_3-x_2+1,\\ h_0 &= x_2x_3+k^2x_2^2-x_3-2k^2x_2. \end{align*}\]
Pitäisi siis osoittaa, että \(h_1=0\) kaikilla \(k\):n arvoilla.
Jos \(AM\) on kulman puolittaja, niin
\[\begin{align*} y_3^2 &= (x_1-x_3)^2+(y_1-y_3)^2\quad\Longrightarrow\\ f_0 &= (k^2+1)x_3^2-1=0. \end{align*}\]
Vastaavasti jos \(BN\) on kulman puolittaja, niin
\[\begin{align*} y_2^2 &= (x_1-x_2)^2+(y_1-y_2)^2\quad\Longrightarrow\\ f_1 &= (k^2+1)x_2^2-2(k^2+1)x_2+1=0. \end{align*}\]
Mutta nyt voidaan tarkistaa, että
\[h_1=(x_2-1)f_0+k^2x_3f_1,\]
mikä todistaa väitteen.
Tässä saadaan myös bonustulos. Huomataan, että jos \(\alpha\) ja \(\beta\) ovat polynomin \(f_1\) nollakohdat, ja jos oletetaan, että \(\alpha<\beta\), niin
\[0<\alpha<1<\beta<2.\]
Tapaus \(\alpha\) vastaa kuvaa 1, ja tapaus \(\beta\) puolestaan kuvaa 2. Väite siis pätee molemmissa tapauksissa, koska polynomien kannalta laskut ovat samat. \(\Box\)
Edellisen esimerkin laskut ovat tietysti työläitä käsin laskien, mutta ne ovat sinänsä helppoja: lasketaan milloin piste on suoralla, tai missä kaksi suoraa leikkaa tai milloin kaksi janaa ovat yhtä pitkiä. Lisäksi laskussa ei varsinaisesti tarvinnut keksiä mitään erityisiä niksejä: piti vain muotoilla haluttu väite polynomiyhtälönä \(h=0\), minkä jälkeen kärsivällisesti laskettiin, että tosiaankin \(h=0\).
Katsotaan sitten esimerkki, jossa esiintyy myös ympyrä. Tätä varten on ensin kätevää johtaa eräs kaava.
Diskriminantti
Alkeisgeometrian tehtävissä usein esiintyy tilanne, jossa suora sivuaa ympyrää. Katsotaan miten tälle saadaan ehto. Olkoon annettu polynomi
\[f=c_2x^2+c_1x+c_0,\]
ja haluttaisiin tutkia, milloin \(f\):llä on kaksinkertainen nollakohta. Olkoot nollakohdat \(\alpha\) ja \(\beta\); polynomin \(f\) diskriminantti on
\[\delta=\delta(f)=c_2^2(\alpha-\beta)^2=c_1^2-4c_0c_2.\]
Mistä tuo viimeinen yhtäsuuruus tulee? Muistetaan viime kerralta [10], että ei lasketa nollakohtia, vaan lasketaan nollakohdilla. Koska \(\alpha\) ja \(\beta\) ovat nollakohtia, niin
\[\begin{align*} & c_2x^2+c_1x+c_0=c_2(x-\alpha)(x-\beta)\quad\Longrightarrow\\[2pt] & \begin{cases} \alpha+\beta=-c_1/c_2\\ \alpha\beta=c_0/c_2. \end{cases} \end{align*}\]
Toisaalta
\[\begin{align*} & \begin{cases} c_2\alpha^2+c_1\alpha+c_0=0\\ c_2\beta^2+c_1\beta+c_0=0 \end{cases}\quad\Longrightarrow\\[2pt] &c_2(\alpha^2+\beta^2)=-2c_0-c_1(\alpha+\beta)=-2c_0+c_1^2/c_2. \end{align*}\]
Siispä
\[\begin{align*} \delta(f) = c_2^2(\alpha-\beta)^2=c_2^2(\alpha^2+\beta^2-2\alpha\beta) = c_1^2-4c_0c_2. \end{align*}\]
Selvästi siis \(f\):llä on kaksinkertainen nollakohta, jos ja vain jos \(\delta=0\). Tämän idean avulla voidaan laskea, milloin suora sivuaa ympyrää. Olkoon annettu
\[\begin{align*} &e_1x+e_2y+e_0=0,\\ &(x-p_1)^2+(y-p_2)^2-r^2=0. \end{align*}\]
Jos \(e_2\ne 0\) ja eliminoidaan \(y\), niin saadaan polynomi
\[\begin{align*} f &=c_2x^2+c_1x+c_0=0,\\ c_2 &=e_1^2+e_2^2,\\ c_1 &= 2\big(e_1e_2p_2-e_2^2p_1+e_1e_0\big), \\ c_0 &=\big(e_2p_2+e_0\big)^2+e_2^2(p_1^2-r^2). \end{align*}\]
Suora sivuaa ympyrää, jos suoralla ja ympyrällä on täsmälleen yksi leikkauspiste. Tällöin \(f\):llä täytyy olla kaksinkertainen nollakohta, joten sen diskriminantin täytyy olla nolla. Nyt suoraan laskemalla saadaan
\[\begin{equation*} \begin{split} \delta(f) &=c_1^2-4c_0c_2=-4e_2^2\delta_0,\\ \delta_0 &=\big(e_1p_1+e_2p_2+e_0\big)^2 -(e_1^2+e_2^2)r^2. \end{split} \tag{1} \end{equation*}\]
Oletuksen mukaan \(e_2\ne 0\), joten suora sivuaa ympyrää, jos \(\delta_0=0\). Jos oletettaisiin \(e_1\ne 0\) ja eliminoitaisiin \(x\), niin päädyttäisiin samaan tulokseen.
Huomaa, että ehto \(\delta_0=0\) tarkoittaa, että suoran \(e_1x+e_2y+e_0=0\) kohtisuora etäisyys pisteestä \(p=(p_1,p_2)\) on \(r\). Joka tapauksessa tässä laskettiin tangentti käyttämättä derivaattoja. Yleisemminkin voitaisiin jonkin käyrän tangentti määritellä ilman derivaattoja vetoamalla leikkauksen moninkertaisuuteen. Siirrytään nyt kuitenkin tarkastelemaan esimerkkejä.
Esimerkkejä

Esimerkki 3. Seuraava tehtävä oli pohjoismaitten matematiikkakilpailussa vuonna 2007. Väitetään, että kuvan 3 tapauksessa
\[AP\cdot BC=2\,AB\cdot PC,\]
missä siis esimerkiksi \(AB\) on pisteitten \(A\) ja \(B\) välinen etäisyys.
Ensimmäinen askel, kuten edellisessä esimerkissä, on kirjoittaa todistettava väite muodossa \(h=0\), missä \(h\) on jokin polynomi.
Olkoon \(A\) origo, ja olkoon \(kx-y=0\) pisteitten \(A\), \(B=(x_2,y_2)\), \(P=(x_1,y_1)\) ja \(C=(x_3,y_3)\) kautta kulkeva suora.4 Siispä
\[\begin{align*} AP^2 &=(1+k^2)x_1^2\\ AB^2 &=(1+k^2)x_2^2,\\ BC^2 &=(1+k^2)(x_2-x_3)^2,\\ PC^2 &=(1+k^2)(x_1-x_3)^2. \end{align*}\]
Olkoon edelleen
\[\begin{align*} h &=\frac{AP^2\cdot BC^2-4\,AB^2\cdot PC^2}{(1+k^2)^2}\\&= x_1^2(x_2-x_3)^2-4x_2^2(x_1-x_3)^2=-h_0h_1,\\ h_0&=2x_2x_3-x_1(x_3+x_2),\\ h_1&=2x_2x_3+x_1(x_3-3x_2). \end{align*}\]
Pitäisi siis osoittaa, että joko \(h_0=0\) tai \(h_1=0\).
Valitaan \(T=(1,0)\), ja olkoot ympyrän säde \(r\) ja \(S=(x_0,y_0)\). Tällöin pisteitten \(A\) ja \(S\) kautta kulkeva suora on \(y_0x-x_0y=0\) ja ympyrän yhtälö on
\[f_0=(x-1)^2+(y-r)^2-r^2=0\ .\]
Kaavan (1) perusteella suora sivuaa ympyrää, jos
\[\delta_0=-y_0(r^2y_0-y_0+2rx_0)=0.\]
Koska \(y_0\ne0\), niin saadaan yhtälöt
\[\begin{align*} &\begin{cases} r^2y_0-y_0+2rx_0=0\\ (x_0-1)^2+(y_0-r)^2-r^2=0 \end{cases}\quad \Longrightarrow\\[2pt] &\big( x_0,y_0\big)=\left(\frac{1-r^2}{1+r^2}, \frac{2r}{1+r^2}\right). \end{align*}\]
Huomataan, että piste \(S\) on aina yksikköympyrällä: \(x_0^2+y_0^2=1\). Suora, joka kulkee \(T\):n kautta, on muotoa \(x+cy-1=0\), ja nyt sijoittamalla \((x_0,y_0)\) saadaan, että se kulkee myös \(S\):n kautta, jos \(c=r\). Nyt piste \(P=(x_1,y_1)\) saadaan ratkaisemalla
\[\begin{cases} x_1+ry_1-1=0\\ kx_1-y_1=0 \end{cases}\quad\Rightarrow\quad \begin{cases} \displaystyle x_1=\frac{1}{kr+1}\\[6pt] \displaystyle y_1=\frac{k}{kr+1}. \end{cases}\]
Sijoittamalla pisteet \(B\) ja \(C\) ympyrän yhtälöön nähdään, että \(x_2\) ja \(x_3\) ovat polynomin
\[f_1= (k^2+1)x^2-2(kr+1)x+1\]
nollakohdat. Siis \(x_2+x_3=2(kr+1)/(k^2+1)\) ja \(x_2x_3=1/(k^2+1)\), joten
\[h_0=\frac{2}{k^2+1}-\frac{1}{kr+1}\frac{2(kr+1)}{k^2+1}=0,\]
ja väite on todistettu.
Tästä saadaan myös bonustulos, kuten edellisessäkin esimerkissä. Huomaa, että missään vaiheessa ei tarvittu sitä, onko \(x_2<x_3\) vai \(x_3<x_2\). Toisin sanoen, jos “vaihdetaan” \(B\) ja \(C\), niin tulos on edelleen voimassa:
\[AP\cdot BC=2\,AC\cdot PB.\] \(\Box\)
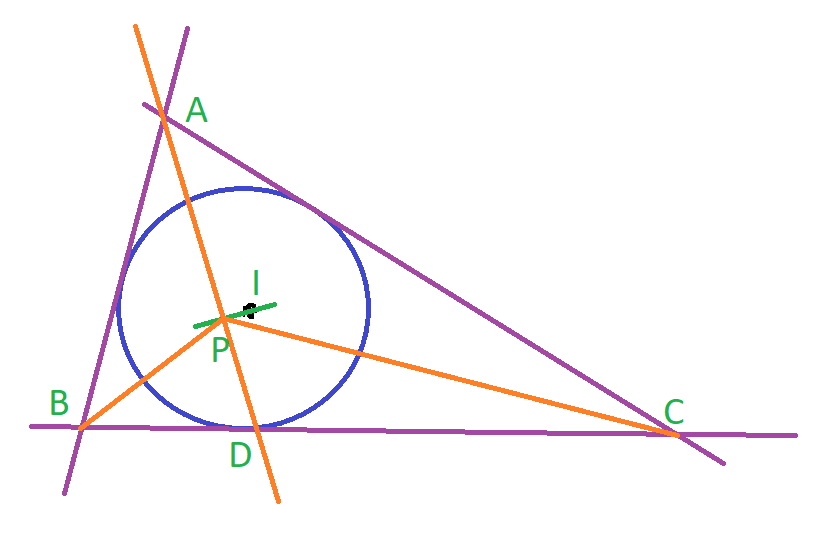
Esimerkki 4. Toinen samantyyppinen esimerkki löytyi oppaasta [6 s. 56], kuva 4. Hauskasti tässä saadaan sama ympyrän yhtälö kuin edellisessä esimerkissä.
Olkoot \(\alpha\) kulma \(BPD\) ja \(\beta\) kulma \(DPC\). Väitetään, että itse asiassa \(\alpha=\beta\). Olkoon
\[h=\sin(\alpha-\beta),\]
ja haluttaisiin siis osoittaa, että \(h=0\). Nyt \(h\) pitäisi ilmaista jotenkin polynomina.
Olkoot \(B\) origo, \(D=(1,0)\), \(C=(x_0,0)\), \(A=(x_1,y_1)\) ja \(P=(x_2,y_2)\). Olkoon edelleen \(r\) ympyrän säde, jolloin \(I=(1,r)\), ja ympyrän yhtälö on taas
\[f_0=(x-1)^2+(y-r)^2-r^2=0.\]
Olkoon \(Q=(x_2,0)\) ja olkoot \(\theta_0\) kulma \(BPQ\), \(\theta_1\) kulma \(QPD\) ja \(\theta_2\) kulma \(QPC\). Selvästi \(\alpha=\theta_0+\theta_1\) ja \(\beta=\theta_2-\theta_1\). Merkitään
\[\begin{align*} c_0=&\cos(\theta_0),\quad s_0=\sin(\theta_0),\\ c_1=&\cos(\theta_1),\quad s_1=\sin(\theta_1),\\ c_2=&\cos(\theta_2),\quad s_2=\sin(\theta_2). \end{align*}\]
Käyttäen hyväksi sitä, että \(c_j^2+s_j^2-1=0\), voidaan nyt suoraviivaisesti laskea, että
\[h=(1-2s_1^2)(s_0c_2-s_2c_0)+ 2c_1s_1(s_0s_2+c_0c_2).\]
Nyt \(h\) on polynomi ja voidaan edetä kuten edellisissä esimerkeissä.
Olkoot edelleen
\[\begin{align*} d_0^2 &=x_2^2+y_2^2,\\ d_1^2 &=(1-x_2)^2+y_2^2,\\ d_2^2 &=(x_0-x_2)^2+y_2^2. \end{align*}\]
Siispä
\[\begin{align*} c_0=&y_2/d_0,\quad s_0=x_2/d_0,\\ c_1=&y_2/d_1,\quad s_1=(1-x_2)/d_1,\\ c_2=&y_2/d_2,\quad s_2=(x_0-x_2)/d_2. \end{align*}\]
Sijoittamalla nämä saadaan
\[\begin{align*} h_0 &=\frac{d_0d_1^2d_2h}{y_2}\\ &=2(1-x_2)y_2^2+d_1^2(2x_2-x_0) -2x_2^3 \: +\\ & \phantom{ = t}6x_2^2-2(x_0+2)x_2+2x_0\\ &=(2-x_0)y_2^2+(2-x_0)x_2^2-2x_2+x_0. \end{align*}\]
Nyt ollaan jo päästy eroon kulmamuuttujista. Lisäksi \(x_0\) on parametri, joka voidaan valita vapaasti, joten \(h_0\):n pitäisi olla nolla kaikilla \(x_0\). Pitäisi vielä laskea \((x_2,y_2)\).
Pisteen \(D\) kautta kulkeva suora on \(x+k_0y-1=0\) ja pisteen \(I\) kautta kulkeva suora, joka on kohtisuorassa tätä suoraa vastaan, on \(k_0x-y+r-k_0=0\). Siispä
\[\begin{cases} x_2+k_0y_2-1=0\\ k_0x_2-y_2+r-k_0=0 \end{cases}\ \Rightarrow\ \begin{cases} \displaystyle x_2=\frac{k_0^2-k_0r+1}{k_0^2+1}\\[8pt] \displaystyle y_2=\frac{r}{k_0^2+1}. \end{cases}\]
Tästä saadaan
\[\begin{align*} h_1=\frac{(k_0^2+1)}{r}h_0 =(2k_0-r)x_0+2r-2k_0. \end{align*}\]
Myös \(r\) on parametri, joka voidaan valita vapaasti, joten pitäisi osoittaa, että \(h_1=0\) kaikilla \(x_0\) ja \(r\). Pitää vielä laskea \(k_0\).
Suora \(x+k_1y-x_0= 0\) kulkee pisteen \(C\) kautta, ja pitäisi laskea \(k_1\) siten, että suora sivuaa ympyrää. Käytetään taas kaavaa (1):
\[\begin{align*} \delta_0 &= (x_0-1)^2-r^2+2k_1r(1-x_0)=0,\\ k_1&= \frac{(x_0-1)^2-r^2}{2r(x_0-1)}. \end{align*}\]
Esimerkin [3] perusteella pisteitten \(A\) ja \(B\) kautta kulkeva suora on
\[2rx-(1-r^2)y=0,\]
joten nyt voidaan laskea \(A\):n koordinaatit:
\[\begin{align*} &\begin{cases} 2rx_1-(1-r^2)y_1=0\\ 2r(x_0-1)(x_1-x_0)+\big((x_0-1)^2-r^2\big)y_1=0 \end{cases}\\[2pt] &\ \Longrightarrow\quad \begin{cases} \displaystyle x_1=\frac{(1-r^2)(x_0-1)}{x_0-r^2-1}\\[8pt] \displaystyle y_1=\frac{2r(x_0-1)}{x_0-r^2-1}. \end{cases} \end{align*}\]
Tästä sitten saadaan
\[k_0=\frac{1-x_1}{y_1}=\frac{r(x_0-2)}{2(x_0-1)}.\]
Sijoittamalla \(k_0\) \(h_1\):n lausekkeeseen nähdään, että \(h_1=0\), mikä todistaa väitteen. \(\Box\)
Polynomit ja Eukleideen geometria: teoria
Edellä polynomit tulivat esille eräänlaisena laskennallisena työkaluna. Konkreettisessa ongelmassa systemaattisesti laskettiin polynomien avulla, mikä johti ratkaisuun. Polynomit kuitenkin valaisevat myös Eukleideen systeemin teoreettisia ominaisuuksia. Esimerkiksi matemaatikkoja varsin pitkään vaivasi seuraava ongelma: voidaanko luku \(\sqrt[3]{2}\) konstruoida harpilla ja viivottimella?
Polynomien avulla nähdään varsin helposti, että tämä on mahdotonta. Alkeisgeometrian konstruktioissa “uusia” pisteitä saadaan joko suorien leikkauspisteestä, suoran ja ympyrän leikkauspisteestä tai kahden ympyrän leikkauspisteistä. Pitää siis tarkistaa nämä kolme tapausta:
Kahden suoran leikkaus:
\[\begin{align*} &a_1x+b_1y+c_1 =0,\\ &a_2x+b_2y+c_2 =0. \end{align*}\]
Jos luvuissa \(a_j\), \(b_j\) ja \(c_j\) ei esiinny kuutiojuuria, niin niitä ei selvästi voi ilmestyä lukuihin \(x\) ja \(y\).
Suoran ja ympyrän leikkaus
\[\begin{align*} & ax+by+c=0,\\ &(x-x_0)^2+(y-y_0)^2-r^2=0. \end{align*}\]
Nyt saadaan, että
\[\begin{cases} x=h_1(a,b,c,x_0,y_0,r)\pm \sqrt{h_2(a,b,c,x_0,y_0,r)},\\ y=-(ax+c)/b, \end{cases}\]
missä \(h_1\) ja \(h_2\) ovat rationaalifunktioita, siis funktioita, jotka ovat muotoa \(p/q\), missä \(p\) ja \(q\) ovat polynomeja. Jälleen jos vakiot eivät alunperin sisällä kuutiojuuria, niin myöskään \(x\) ja \(y\) eivät sisällä kuutiojuuria.
Kahden ympyrän leikkaus
\[\begin{align*} &f_1= (x-x_0)^2+(y-y_0)^2-r_0^2=0,\\ &f_2= (x-x_1)^2+(y-y_1)^2-r_1^2=0. \end{align*}\]
Tästä saadaan
\[f_1-f_2=2(x_1-x_0)x+2(y_1-y_0)y+d,\]
missä
\[d=x_1^2-x_0^2+y_1^2-y_0^2+r_1^2-r_0^2.\]
Mutta \(f_3=f_1-f_2=0\) on suoran yhtälö, ja koska systeemi \(f_1=f_2=0\) on ekvivalentti systeemin \(f_1=f_3=0\) kanssa, niin tämä tapaus palautuu tapaukseen 2.
Täsmällinen lause, jossa yleisemminkin karakterisoidaan, mitkä luvut saadaan harpilla ja viivottimella, löytyy kirjasta [2, Theorem 10.1.6]. Lauseen todistus perustuu täysin yllä mainittuihin kolmeen kohtaan.
Tästä muuten myös nähdään, että viivotin on turha: kaikki konstruktiot voidaan tehdä pelkästään harpilla. Tämä seuraa kohdasta 3: koska kahden ympyrän “erotus” on suora/viivotin, niin viivotinta voidaan aina “simuloida” ympyröillä/harpeilla.
Tavallaan voisi sanoa, että Eukleideen systeemi oli jotenkin sopivasti sekä yksinkertainen että monipuolinen. Yksinkertainen siinä mielessä, että systeemin kokonaisuus ei levinnyt käsistä, ja monipuolinen siinä mielessä, että systeemin avulla kuitenkin saatiin paljon mielenkiintoisia tuloksia.
Eukleideen systeemissä otettiin kaksi käyrää, suora ja ympyrä, eräänlaisina annettuina muotoina, tai algoritmisesti eräänlaisina alkeisoperaatioina, jotka voidaan aina tehdä äärellisessä ajassa. Eukleideen konstruktion vaativuus voitaisiin nyt ajatella (painotettuna) summana tehtävässä tarvittavista viivotin- ja harppioperaatioista. Uskoisin, että Eukleides, kuten nykymatemaatikotkin, olisi pitänyt konstruktiota eleganttina, jos siinä on mahdollisimman vähän alkeisoperaatioita. Nykyisin tämänkaltaisia kysymyksiä tutkitaan laskennallisessa geometriassa.5
Eukleideen systeemin laajentaminen yleisempien tasokäyrien analyysiin on kuitenkin hankalaa. Nythän esimerkiksi voitaisiin ajatella, että paraabelin piirtäminen olisi myös alkeisoperaatio. Tästä saadaan selvästi vahvempi systeemi, koska kuutiojuuri saadaan nyt helposti: paraabelit
\[\begin{align*} & y-x^2=0,\\ & x-2y^2=0 \end{align*}\]
leikkaavat origon lisäksi pisteessä \(\big(\sqrt[3]{2},\sqrt[3]{4}\big)\). Tiettävästi Menaechmus6 ratkaisi kuutiojuuriongelman juuri näin kahden paraabelin leikkauksen avulla noin vuonna 350 eaa.
Mutta kuinka vahva näin saatu systeemi olisi? Mitä kaikkea tällaisella systeemillä voisi tehdä? Koska ei ollut mitään algebrallista tai muutakaan tapaa tarkastella yleisiä käyriä, niin monilla käyrillä oli jonkinlainen mekaaninen tai kinemaattinen määritelmä. Arkhimedeen spiraali saadaan, kun kiinnitetään teleskooppivavan toinen pää origoon, minkä jälkeen vavan pituus kasvaa vakionopeudella ja vapa pyörii vakiokulmanopeudella.7 Traktrix puolestaan saadaan, kun vedetään pulkkaa narusta.8
Albrecht Dürer jopa konkreettisesti rakensi laitteen, jolla voidaan piirtää eräs käyrä, jota nykyään luonnollisesti sanotaan Dürerin käyräksi (Dürer’s shell curve tai conchoid of Dürer).9 Kuva 5 on peräisin Dürerin kirjasta Underweysung der Messung vuodelta 1525 [4].

Nyt voitaisiin kysyä, voidaanko esimerkiksi Arkhimedeen spiraali konstruoida, jos käytössä on suorat, ympyrät ja paraabelit? Tai voidaanko paraabeli konstruoida, jos on suorat, ympyrät ja spiraalit? Ylipäätään tasokäyriin liittyvissä ongelmissa tangentin laskeminen/määrittäminen oli luonnollinen ja usein esiintyvä tehtävä. Ympyrälle tangentti saadaan Eukleideen systeemillä, mutta kaikille muille käyrille tämä oli vaikeaa. Kaiken lisäksi jos yhdelle käyrälle saatiin tangentti, niin tästä ei ollut välttämättä mitään hyötyä, kun tarkasteltiin jotain muuta käyrää. Jokainen käyrä vaati oman teoriansa. Ei siis ole ihme, että klassinen geometria ajautui umpikujaan. Geometrian umpikujavaihe kestikin sitten noin 1500 vuotta, kunnes analyyttinen geometria ja differentiaalilaskenta muuttivat kaiken.
Eukleideen systeemi ja opetus
Vaikka Eukleideen systeemi ei mitenkään rajoitu geometriaan, niin nykyään on tapana puhua nimenomaan Eukleideen geometriasta ja esittää kaikki muu materiaali moderneja käsitteitä ja merkintöjä käyttäen. Esimerkiksi Alkeitten toisen luvun 7. lause osoittaa, että
\[x^2+y^2=2xy+(x-y)^2\]
ja algoritmi suurimman yhteisen tekijän laskemiseksi on Alkeitten 7. luvun toisessa lauseessa.10 Tuskinpa kukaan pitäisi mielekkäänä todistaa tai edes muotoilla näitä tuloksia kuten Eukleides. Samoin Pythagoraan lause (1. luvun 47. lause) voidaan helposti todistaa vektoreitten avulla.
Hiukan paradoksaalisesti siis usein painotetaan Eukleideen systeemin aksiomaattista luonnetta, vaikka kaikki tehtävät mitä opetuksessa/kilpailuissa käytetään ovat intuitiivisesti geometrisia, siis sellaisia, joista voi piirtää mielekkään ja mielenkiintoisen kuvan. Esimerkkinä epäilyttävästä tehtävästä olisi vaikkapa luvun
\[\alpha=\sqrt{1+\sqrt{2+\sqrt{3+\sqrt{5}}}}\]
konstruointi. Eukleideen systeemissä tämä voidaan selvästi tehdä. Tietääkseni tähän lukuun ei liity mitään erityistä geometrista (tai muutakaan) ominaisuutta, ja luulisin, että lukija nimenomaan intuitiivisesti (eikä aksiomaattisesti) ymmärtää, mitä tarkoitan geometrisella ominaisuudella.
Tämän takia ei oikeastaan opetuksen kannalta ole varsinaista merkitystä sillä, että aksioomasysteemiä piti hiukan paikata, kun tätä sitten 1800-luvun lopussa modernista näkökulmasta tarkemmin analysoitiin [5, 7]. Esimerkiksi Eukleides heti ensimmäisen luvun ensimmäisen lauseen todistuksessa olettaa eräitä asioita, jotka eivät seuraa aksioomista, mutta jotka ovat intuitiivisesti ja visuaalisesti selviä.
Eukleideen geometriaa voidaan tavallaan pitää eräänlaisena pelinä. Kuten edellä oli puhetta, pelin säännöt ovat riittävän yksinkertaiset, ja opetuksen kannalta on mielenkiintoista, että pelin kulku (eli eteneminen sallittujen siirtojen puitteissa kohti haluttua tavoitetta) voidaan visualisoida piirrosten avulla. Tietenkin kaikkiin Eukleideen konstruktioihin voidaan liittää jokin kuvio, mutta peliin valitaan vain sellaisia tehtäviä, joilla on “oikeasti” intuitiivinen geometrinen sisältö, jolloin myös pelaaja kokee mielekkääksi hahmottaa tilannetta kuvan avulla visuaalisesti.
Lisäksi todistettavien tulosten vaikeusaste vaihtelee suuresti, joten peliä voidaan pelata eri tasoilla (vai pitäisikö nykyään sanoa leveleillä). René Thom ilmaisee asian näin [8]:
Only those topics which have a quality of “play” have educational value, and of all such games, Euclidean geometry, with its constant references to underlying intuitively understood fundamentals, is the least gratuitous and the richest in meaning.11
Lopuksi
Esimerkeissä tarkasteltu laskennallinen ratkaisumenetelmä voi olla hyvin työläs käsin laskien; etenkin esimerkin 4 ratkaisu käsin tuolla tavalla olisi ollut käytännössä mahdotonta ainakin jossain kokeessa tai kilpailussa. Toisaalta kaikki yllä olevat laskut olivat hyvin helppoja esimerkiksi wxMaximalla, tai jollain muulla laskentaohjelmalla. Ne olivat nimenomaan vain työläitä, mutta periaatteessa helppoja, kuten vaikkapa kahden hyvin ison kokonaisluvun tulon laskeminen. Ainoa ongelma on lähinnä, että jos ei ole tottunut tällaiseen ongelmanratkaisuun, niin tarvittavien muuttujien/parametrien suuri määrä voi alussa sekoittaa.
Esimerkeissä 2, 3 ja 4 ei siis tarvinnut käyttää varsinaista geometrista intuitiota, vaan todistuksessa edettiin systemaattisesti ikään kuin lopusta alkuun. Ensin muotoiltiin haluttu väite polynomiyhtälönä \(h=0\). Sitten katsottiin, mistä muuttujista \(h\) riippuu, laskettiin muuttujien arvot, ja lopuksi havaittiin, että todellakin \(h=0\) pätee. Kehotan lukijoita vertaamaan “alkuperäisiin” todistuksiin. Varmasti jotkut pitävät geometrista todistusta parempana, ehkäpä esteettisistä syistä. Jätän harjoitustehtäväksi vielä sen pohtimisen, saadaanko bonustulokset helposti perustapauksen todistuksesta vai pitääkö aloittaa kaikki alusta.
Geometrinen todistus voi vaatia jonkin näppärän idean keksimistä, ja tällaisen idean löytäminen onkin palkitsevaa, ja parhaassa tapauksessa idean ymmärtäminen auttaa hahmottamaan yleisestikin tietynlaisia tehtävätyyppejä. Toisaalta varmaankin jokainen lukija, kuten minä, on joskus (tai ehkä pikemminkin aivan liian usein) tuskaillut jonkin ongelman parissa, etsien turhaan sitä näppärää ideaa. Tällaisissa tilanteissa ainakin minusta on kivaa, että on menetelmä, jonka avulla ratkaisu varmasti löytyy.
Tietysti jos pelin säännöt vaativat Eukleideen systeemin käyttämistä, niin sitten pitää pelata sääntöjen mukaan. En tiedä hylätäänkö kilpailuissa vastaus, jos käytetään “vääriä” menetelmiä? Joka tapauksessa jos jossain ikään kuin luonnollisessa projektissa tulee vastaan geometrinen osaongelma, niin uskoisin, että polynomien käyttäminen olisi varsin luontevaa, koska tyypillisesti pelkkä Eukleideen geometria ei kuitenkaan riitä koko ongelman ratkaisuun.
Ensi kerralla palataan algebrallisempiin aiheisiin, ja katsotaan, miten jakolaskun avulla voidaan analysoida polynomiepäyhtälöitä. Lisäksi tutustutaan erääseen varsin moderniin menetelmään, jota on viime aikoina tutkittu paljon, ja jolla on yhteyksiä myös konveksiin geometriaan ja optimointiin.
Viitteet
[1] G. V. Bard, Sage for undergraduates, 2nd ed., American Mathematical Society, 2022.
[2] D. A. Cox, Galois theory, 2nd ed., Pure and Applied Mathematics (Hoboken), John Wiley & Sons, 2012.
[3] D. A. Cox, J. Little, and D. O’Shea, Ideals, varieties, and algorithms, 4th ed., Undergraduate Texts in Mathematics, Springer, Cham, 2015, An introduction to computational algebraic geometry and commutative algebra.
[4] A. Dürer, Géometrie (Underweysung der Messung), Seuil, 2016, käännös, johdanto ja kommentit J. Peiffer.
[5] R. Hartshorne, Geometry: Euclid and beyond, Undergraduate Texts in Mathematics, Springer-Verlag, New York, 2000.
[6] O. Järviniemi, Ollin opas olympiatason ongelmanratkaisuun, https://matematiikkakilpailut.fi/aiheet/.
[7] M. Lehtinen, Geometrian perusteita, https://docplayer.fi/28732077-Geometrian-perusteita-matti-lehtinen.html.
[8] R.Thom, ‘’Modern’’ mathematics: An educational and philosophic error?, American Scientist 59 (1971), no. 6, 695–699.
[9] J. Tuomela, Tarinoita polynomeista (osa 1), Solmu (2022), no. 2.
[10] J. Tuomela, Tarinoita polynomeista (osa 2), Solmu (2022), no. 3.
Alaviitteet
Lyhin korkeusjana vastaa pisintä sivua, mutta jos tätä ei muista, niin nyt on helppo laskea myös muitten korkeusjanojen pituudet, kun \(p_2\) tunnetaan.↩︎
Jätän harjoitustehtäväksi tapauksen, jossa \(x_1=x_2=x_3=0\).↩︎
https://mathshistory.st-andrews.ac.uk/Biographies/Menaechmus/↩︎
Sana play on ehkä lainausmerkeissä sen takia, että sitä vastasi alkuperäisessä kirjoituksessa ludique, mikä viittaa nimenomaan leikkimiseen eikä pelaamiseen.↩︎