Ymmärryksen tuolla puolen
Jukka Liukkonen
Mat. yo. evp.
Young man, in mathematics you don’t understand things. You just get used to them.
— John von Neumann
Moniulotteinen maailma
Liitin tuon epigrafin artikkelin alkuun siksi, että en ymmärrä neliulotteista avaruutta, saati sitten useampiulotteista avaruutta. Kolmiulotteisen avaruuden luulen ymmärtäväni, mutta saatan olla Dunning-Kruger-efektin eli ylivertaisuusvinouman uhri. Kun kolme koordinaattiakselia laitetaan kohtisuoraan toisiaan vastaan, ja siihen pitäisi ängetä neljäs akseli, joka on kohtisuorassa kaikkia kolmea vastaan, niin en kyllä ymmärrä, mihin suuntaan se neljäs akseli sojottaa. Kuitenkin pääsin yliopistossa esimerkiksi matriisilaskennan kurssista läpi, vaikka siellä käsiteltiin lineaarisia kuvauksia \(m\)-ulotteiselta avaruudelta \(n\)-ulotteiseen avaruuteen, missä \(m\) ja \(n\) voivat olla miten suuria positiivisia kokonaislukuja tahansa. Jotain kummallista tässä matematiikassa on. Sen avulla pystytään tunkeutumaan ihmisen havaintomaailman ja käsityskyvynkin tuolle puolen. Lisäksi tuo tunkeutuminen on aika usein yhtä vaivatonta kuin omenoiden, banaanien ja appelsiinien jaottelu eri koreihin.
Tiesitkö muuten, että kaikki solmut [4] aukeavat neliulotteisessa avaruudessa? Tai oikeastaan ne ovat jo valmiiksi auki sellaisen tarkkailijan mielestä, joka ei ole sidottu kolmeen ulottuvuuteen. Tätä aihetta käsitellään artikkelin lopussa. Alkuosassa pohditaan eriulotteisten kappaleiden mittaamista.
Moniulotteisen kuution pinta-ala ja tilavuus
Euklidinen avaruus \({\mathbb R}^3\) on pisteiden \((x_1,x_2,x_3)\) joukko
\[{\mathbb R}^3 = \big\{\,(x_1,x_2,x_3)\;\big|\;x_1,x_2,x_3\in{\mathbb R}\,\big\}.\]
Kun avaruuden ulottuvuuksien määrää kasvatetaan, jono \((x_1,x_2,x_3)\) pitenee jonoksi \((x_1,\ldots,x_n)\), ja yleinen \(n\)-ulotteinen euklidinen avaruus on joukko
\[{\mathbb R}^n = \big\{\,(x_1,\ldots,x_n)\;\big|\;x_1,\ldots,x_n\in{\mathbb R}\,\big\}.\]
Kahden pisteen \(a=(a_1,\ldots,a_n)\) ja \(b=(b_1,\ldots,b_n)\) välinen etäisyys lasketaan Pythagoraan lauseen yleistyksen kautta kuten kolmiulotteisessa avaruudessa:
\[|a-b| = \sqrt{(a_1-b_1)^2+\ldots+(a_n-b_n)^2}.\]
Pituudesta, pinta-alasta ja tilavuudesta käytetään yhteistä nimitystä mitta tai täsmällisemmin \(1\)-mitta, \(2\)-mitta ja \(3\)-mitta. Useampiulotteisessa avaruudessa \({\mathbb R}^n\) puhutaan \(n\)-mitasta. Esimerkiksi \(n\)-ulotteisen suorakulmaisen suuntaissärmiön
\[\big\{\,(x_1,\ldots,x_n)\;\big|\;a_1\le x_1\le b_1,\ldots,a_n\le x_n\le b_n\,\big\}\]
\(n\)-mitta on särmien pituuksien tulo
\[(b_1-a_1)\ldots(b_n-a_n).\]
Muiden kappaleiden voidaan ajatella koostuvan pienenpienistä suorakulmaisista suuntaissärmiöistä. Tähän ajatukseen perustuu pinta-alan mittaaminen neliösenttimetreissä tai tilavuuden mittaaminen kuutiosenttimetreissä. Kun \(n\)-ulotteista kappaletta venytetään niin, että etäisyydet \(r\)-kertaistuvat, kappaleen \(n\)-mitta \(r^n\)-kertaistuu, sillä
\[\begin{split} &r(b_1-a_1)r(b_2-a_2)\ldots r(b_n-a_n) \\ &\quad = r^n(b_1-a_1)(b_2-a_2)\ldots(b_n-a_n). \end{split}\]
Moniulotteisen avaruuden olioita nimitetään hyperolioiksi: esimerkiksi \(n\)-ulotteisen avaruuden \(n\)-ulotteinen kuutio on hyperkuutio [2], kolmiulotteisessa avaruudessa leijuvaa kaksiulotteista tasoa vastaa \(n\)-ulotteisen avaruuden \((n{-}1)\,\)-ulotteinen hypertaso [3] jne. Origokeskisen hyperkuution
\[C^n_r = \big\{\,(x_1,\ldots,x_n)\;\big|\; {-}r\le x_1\le r,\ldots, -r\le x_n\le r\,\big\}\]
\(n\)-mitta eli hypertilavuus \(V(C^n_r)\) ja hyperpinta-ala \(A(C^n_r)\) ovat
\[V(C^n_r) = (2r)^n \;\;\text{ja}\;\; A(C^n_r) = 2n(2r)^{n-1},\]
sillä hyperkuutiolla on jokaista koordinaattiakselia kohti kaksi \((n{-}1)\,\)-ulotteista hyperkuutiosivutahkoa, joista kummankin \((n{-}1)\,\)-mitta on \(V(C^{n-1}_r)=(2r)^{n-1}\). Hyperkuution lävistäjän pituus on
\[d(C^n_r) = \sqrt{n(2r)^2} = 2r\sqrt{n}.\]
Origokeskiselle yksikköhyperkuutiolle \(r=1/2\), ja
\[V(C^n_{1/2}) = 1,\;\; A(C^n_{1/2}) = 2n \;\;\text{ja}\;\; d(C^n_{1/2}) = \sqrt{n}.\]
Huomaa, että yksikköhyperkuution hypertilavuus säilyy vakiona, mutta hyperpinta-ala ja läpimitta kasvavat rajatta, kun avaruuden dimensio \(n\) kasvaa rajatta. Jatkossa puhutaan kuutioista, pinta-aloista, tilavuuksista jne. silloinkin, kun ulottuvuuksia on enemmän kuin kolme. Ulottuvuuksien määrä ilmenee asiayhteydestä.
Moniulotteinen pallo ja kuula
Pallolla tai \((n{-}1)\)-pallolla [5] tarkoitetaan tässä artikkelissa \(n\)-ulotteisen euklidisen avaruuden \({\mathbb R}^n\) pistejoukkoa
\[S^{n-1}_r = \big\{\,(x_1,\ldots,x_n)\;\big|\;x_1^2+\ldots+x_n^2=r^2\,\big\}.\]
Sen pisteet sijaitsevat tasan säteen \(r\) päässä origosta. Pallo käsittää siis pelkän \((n{-}1)\)-ulotteisen pallonkuoren. Kun siihen yhdistetään kuoren sisäpuolelle jäävät pisteet, saadaan kuula eli \(n\)-kuula
\[B^n_r = \big\{\,(x_1,\ldots,x_n)\;\big|\;x_1^2+\ldots+x_n^2\le r\,\big\}.\]
Pallon \((n{-}1)\)-mittaa \(A(S^{n-1}_r)\) sanotaan pallon pinta-alaksi, ja kuulan \(n\)-mittaa \(V(B^n_r)\) kuulan tilavuudeksi. Yksikköpallon tapauksessa pinta-alaa ja tilavuutta merkitään
\[A_{n-1} = A(S^{n-1}_1) \;\;\text{ja}\;\; V_n = V(B^n_1).\]
Ne skaalautuvat \(r\)-säteisen pallon pinta-alaksi ja kuulan tilavuudeksi:
\[A(S^{n-1}_r) = r^{n-1}A_{n-1} \;\;\text{ja}\;\; V(B^n_r) = r^nV_n\,.\]
Kuulan kuorimalli
Tilavuuden laskemiseksi kuulan ajatellaan koostuvan sisäkkäisistä pallonkuorista kuin sipuli. Säteen pituuden lisäystä \(\Delta r\) vastaa tilavuuden lisäys
\[\Delta V(B^n_r)\approx A(S^{n-1}_r)\,\Delta r,\]
joka on pallon pinta-ala kerrottuna pallonkuoren paksuudella. Kun säteen lisäys on hyvin pieni ja lähestyy nollaa, perinteisen havainnollisen ajattelutavan mukaan äärettömän pienille eli infinitesimaalisille erotuksille tai differentiaaleille
\[{\text{d}}r = \lim_{\Delta r\to 0}\Delta r \;\;\text{ja}\;\; {\text{d}}V(B^n_r) = \lim_{\Delta r\to 0}\Delta V(B^n_r)\]
saadaan tarkka yhtälö
\[{\text{d}}V(B^n_r) = A(S^{n-1}_r)\,{\text{d}}r.\]
Tämä on tietysti löysää puhetta, mutta se johtaa päteviin yhtälöihin
\[\lim_{\Delta r\to 0}\,\frac{\Delta V(B^n_r)}{\Delta r} = \frac{{\text{d}}V(B^n_r)}{{\text{d}}r} = A(S^{n-1}_r),\]
joilla on täsmällinen merkitys: pinta-ala on tilavuuden erotusosamäärän raja-arvo, toisin sanoen derivaatta.
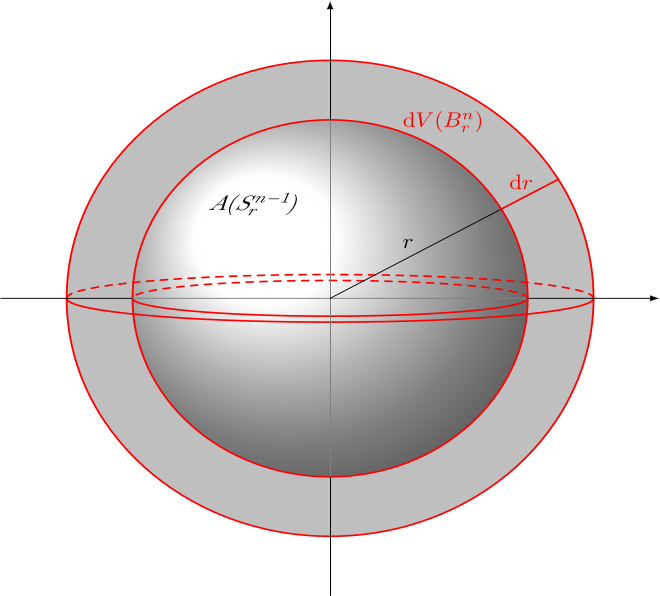
Muutoksen mallintaminen differentiaalien avulla on paljon käytetty ja tehokkaaksi havaittu menetelmä erilaisten kaavojen ja yhtälöiden johtamiseen. Muodollisesta yhtälöstä \({\text{d}}V(B^n_r) = A(S^{n-1}_r)\,{\text{d}}r\) päästään mukavasti integraaliyhtälöön
\[{\int\limits_{0}^{R}}{\text{d}}V(B^n_r) = {\int\limits_{0}^{R}}A(S^{n-1}_r){\text{d}}r,\]
toisin kirjoitettuna ja laskettuna
\[V(B^n_R) = A_{n-1}{\int\limits_{0}^{R}}r^{n-1}{\text{d}}r = \frac{A_{n-1}}{n}{\overset{\hspace{2ex}R}{\underset{\hspace{-2ex}0}{\bigg/}}}r^n = \frac{A_{n-1}}{n}\,R^n.\]
Erityisesti
\[ V_n = \frac{A_{n-1}}{n}. \]
Kuulan siivumalli
Tilavuuksien \(V_n\) ja \(V_{n-1}\) välille saadaan yhteys, kun kuula siivutetaan ohuiksi siivuiksi \(x_n\)-akselia vastaan kohtisuorassa suunnassa kuvan mukaisesti.
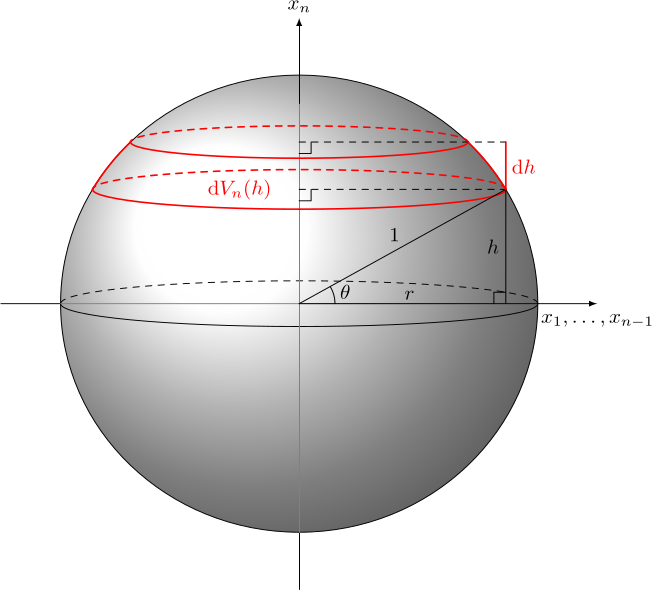
Korkeuden \(h\) muutosta \({\text{d}}h\) vastaava tilavuuden muutos on siivun pinta-alan ja paksuuden tulo
\[\begin{split} {\text{d}}V_n(h) &= V(B^{n-1}_r)\,{\text{d}}h = r^{n-1}V_{n-1}\,{\text{d}}h \\ &= V_{n-1}\cos^{n-1}\theta\;{\text{d}}\sin\theta \\ &= V_{n-1}\cos^n\theta\;{\text{d}}\theta, \end{split}\]
missä \(h=\sin\theta\), \(r=\cos\theta\) ja yleisesti \({\text{d}}f(\theta)=f'(\theta)\,{\text{d}}\theta\). Siivun pinta-alalla tarkoitetaan \((n{-}1)\) -ulotteisen kuulan \((n{-}1)\) -mittaa. Integroimalla saadaan
\[\begin{split} V_n &= 2{\int\limits_{0}^{1}}{\text{d}}V_n(h) = 2V_{n-1}{\int\limits_{0}^{\frac{\pi}{2}}}\cos^n\theta\;{\text{d}}\theta \\ &= V_{n-1}{\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}}}\cos^n\theta\;{\text{d}}\theta = V_{n-1}I_n\,, \end{split}\]
missä on merkitty \(I_n = {\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}}}\cos^n\theta\;{\text{d}}\theta\). Erityisesti \(I_0=\pi\) ja \(I_1=2\). Siis
\[ V_n = V_{n-1}I_n\,,\qquad I_n=\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^n\theta\;{\text{d}}\theta. \]
Pallon siivumalli
Pallon pinta-ala voidaan laskea siivuttamalla samaan tapaan kuin tilavuuskin. Pinta-alojen \(A_n\) ja \(A_{n-1}\) välinen yhteys saadaan integroimalla yhtälöstä
\[{\text{d}}A_n(\theta) = A(S^{n-1}_{\cos\theta})\,{\text{d}}\theta = A_{n-1}\cos^{n-1}\theta\,{\text{d}}\theta.\]
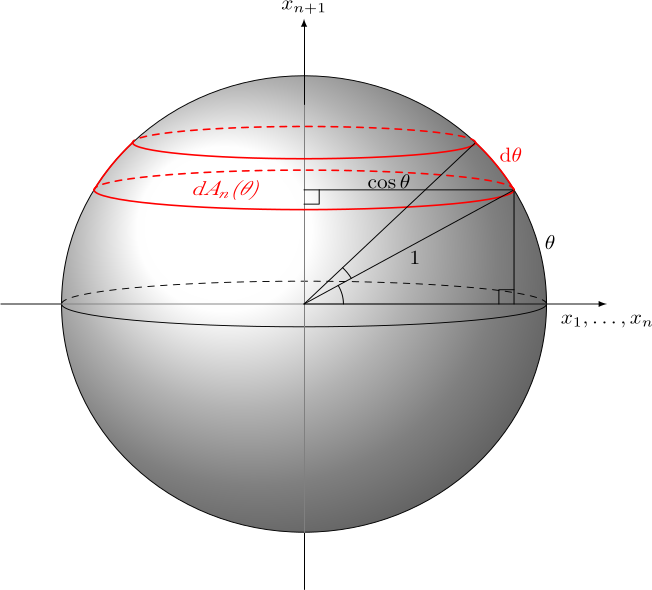
Toisin sanoen
\[A_n = A_{n-1}{\int\limits_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}}}\cos^{n-1}\theta\,{\text{d}}\theta.\]
\[ A_n = A_{n-1}I_{n-1}\,. \]
Kosinin potenssin integraali
Kehystetyistä kaavoista saadaan palautuskaava, josta integraalin \(I_n\) arvot voidaan laskea:
\[\frac{I_{n+1}}{I_{n-1}} = \frac{V_{n+1}}{V_{n}}\,\frac{A_{n-1}}{A_{n}} = \frac{n}{n+1}\,\frac{A_{n}}{A_{n-1}}\frac{A_{n-1}}{A_{n}} = \frac{n}{n+1}\,.\]
Täten parillisilla \(n\)
\[\begin{split} I_{n+1} &= \frac{n}{n+1}\,I_{n-1} = \frac{n}{n+1}\cdot\frac{n-2}{n-1}\cdot\ldots\cdot\frac{2}{3}\,I_1 \\ &= \frac{n\cdot(n-2)\cdot\ldots\cdot 2}{(n+1)\cdot(n-1)\cdot\ldots\cdot 3}\cdot 2, \end{split}\]
ja parittomilla \(n\)
\[\begin{split} I_{n+1} &= \frac{n}{n+1}\,I_{n-1} = \frac{n}{n+1}\cdot\frac{n-2}{n-1}\cdot\ldots\cdot\frac{1}{2}\,I_0 \\ &= \frac{n\cdot(n-2)\cdot\ldots\cdot 1}{(n+1)\cdot(n-1)\cdot\ldots\cdot 2}\cdot\pi. \end{split}\]
Matemaattisten laskelmien ja päätelmien tekemistä voidaan verrata löytöretkeilyyn. Edellä esitetty kosinin potenssin integrointikaavan johto hyperpallojen ja -kuulien avulla muistuttaa purjehdusta Helsingistä Tallinnaan Kap Hornin kautta. Perille päästiin kuitenkin. Puoli vuosituhatta sitten eräs purjehtija lähti etsimään Intiaa, mutta päätyi Amerikkaan. Myös matemaattisella matkalla löydetään kaikkea mielenkiintoista, eikä aina sitä, mitä alun perin oli tarkoitus. Nyt kävi onnekkaasti.
Tehtävä 1. Johda palautuskaava \(I_{n}=\displaystyle\frac{n-1}{n}\,I_{n-2}\) osittaisintegroimalla.
Tehtävä 2. Johda hyperoktaedrin
\[O^n_r = \big\{\,(x_1,\ldots,x_n)\;\big|\;|x_1|+\ldots+|x_n|\le r\,\big\}\]
tilavuuden lauseke. Vihje: Viipaloimalla saat palautuskaavan, jossa \(V(O^n_1)\) lausutaan tilavuuden \(V(O^{n-1}_1)\) avulla.
Gamma-funktio
Pallojen ja kuulien mittaamisessa on edistytty palautuskaavojen tasolle, mutta lopullisten laskentakaavojen aikaansaamiseksi pitää vielä tehdä töitä. Sitä varten määritellään kertomafunktiota \(\ell\mapsto(\ell{-}1)!\) muistuttava gammafunktio
\[\begin{split} &\Gamma: \big\{\,\tfrac{k}{2}\;\big|\;k\in{\mathbb Z},\;k>0\,\big\}\to{\mathbb R}, \\[1ex] &\Gamma\big(\tfrac{k}{2}\big) = \left\{\begin{array}{@{}c@{}c@{\phantom{x}}l} \sqrt{\pi} & , & k=1\,, \\[1ex] 1 &, & k=2\,, \\[1ex] \big(\tfrac{k}{2}-1\big)\,\Gamma\big(\tfrac{k}{2}-1\big) & , & k>2\,. \end{array}\right. \end{split}\]
Olkoon \(k\) parillinen. Kun palautuskaavaa (alin vaihtoehto) sovelletaan \(k/2\) kertaa, saadaan yhtälö
\[\Gamma\left(\frac{k+2}{2}\right) = \frac{k}{2}\cdot\frac{k-2}{2}\cdot\ldots\cdot\frac{4}{2}\cdot\frac{2}{2}\cdot\Gamma(1),\]
josta ratkeaa
\[k\cdot(k-2)\cdot\ldots\cdot 4\cdot 2 = \frac{2^{\frac{k}{2}}\Gamma\left(\frac{k+2}{2}\right)}{\Gamma(1)} = 2^{\frac{k}{2}}\Gamma\left(\frac{k+2}{2}\right).\]
Parittomilla \(k\) sovelletaan palautuskaavaa \((k{+}1){/}2\) kertaa, mikä johtaa yhtälöön
\[\Gamma\left(\frac{k+2}{2}\right) = \frac{k}{2}\cdot\frac{k-2}{2}\cdot\ldots\cdot\frac{3}{2}\cdot\frac{1}{2}\cdot \Gamma\left(\frac{1}{2}\right).\]
Siitä ratkaistaan
\[k\cdot(k-2)\cdot\ldots\cdot 3\cdot 1 = \frac{2^{\frac{k+1}{2}}\Gamma\left(\frac{k+2}{2}\right)}{\Gamma\left(\frac{1}{2}\right)} = \frac{2^{\frac{k+1}{2}}}{\sqrt{\pi}}\,\Gamma\left(\frac{k+2}{2}\right).\]
Parillisilla \(n\) on täten
\[I_{n+1} = \frac{2^{\frac{n}{2}}\Gamma\left(\frac{n+2}{2}\right)} {\frac{2^{\frac{n+2}{2}}}{\sqrt{\pi}}\,\Gamma\left(\frac{n+3}{2}\right)}\cdot 2 = \frac{\Gamma\left(\frac{n+2}{2}\right)} {\Gamma\left(\frac{n+3}{2}\right)}\,\sqrt{\pi}\,.\]
Parittomilla \(n\) pätee
\[I_{n+1} = \frac{\frac{2^{\frac{n+1}{2}}}{\sqrt{\pi}}\,\Gamma\left(\frac{n+2}{2}\right)} {2^{\frac{n+1}{2}}\Gamma\left(\frac{n+3}{2}\right)}\cdot\pi = \frac{\Gamma\left(\frac{n+2}{2}\right)} {\Gamma\left(\frac{n+3}{2}\right)}\,\sqrt{\pi}\,.\]
Yllättäen saatiin samannäköinen tulos parillisilla ja parittomilla \(n\). Kun \(n\) korvataan erotuksella \(n{-}1\), saadaan yleinen kaava
\[ I_n = \frac{\Gamma\left(\frac{n+1}{2}\right)}{\Gamma\left(\frac{n+2}{2}\right)}\,\sqrt{\pi}\,. \]
On vaivatonta tarkistaa, että se pätee myös tapauksissa \(n=0\) ja \(n=1\).
Huomautus. Erillisissä pisteissä \(k/2\), missä \(k\) on positiivinen kokonaisluku, määritelty funktio \(\Gamma\) voidaan laajentaa kompleksimuuttujan kompleksiarvoiseksi (meromorfi)funktioksi
\[\Gamma: {\mathbb C}\setminus\{0,-1,-2,\ldots\}\to{\mathbb C},\;\; z\mapsto\Gamma(z).\]
Tällöin puhutaan Eulerin gammafunktiosta [1]. Sen rajoittumana saadaan jatkuva funktio
\[\Gamma:\,]0,\infty[\,\to{\mathbb R},\]
jolle \(\Gamma(\ell)=(\ell-1)!=1\cdot 2\cdot\ldots\cdot(\ell-1)\) kaikilla positiivisilla kokonaisluvuilla \(\ell\).
Pallon pinta-ala ja kuulan tilavuus
Palautuskaavaa toistamalla saadaan pallon pinta-alaksi
\[\begin{split} A_n &= A_{n-1}I_{n-1} = A_{n-2}I_{n-2}I_{n-1} = \ldots \\ &= A_1I_1\ldots I_{n-2}I_{n-1} = 2\pi I_1\ldots I_{n-2}I_{n-1}. \end{split}\]
Tulolla \(I_1\ldots I_{n-1}\) on lauseke
\[\begin{split} I_1\ldots I_{n-1} &= \pi^\frac{n-1}{2}\,\frac{\Gamma\left(1\right)}{\Gamma\left(\frac{3}{2}\right)} \frac{\Gamma\left(\frac{3}{2}\right)}{\Gamma\left(2\right)} \frac{\Gamma\left(2\right)}{\Gamma\left(\frac{5}{2}\right)}\ldots \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n+1}{2}\right)} \\[1ex] &= \frac{\pi^\frac{n-1}{2}}{\Gamma\left(\frac{n+1}{2}\right)}\,. \end{split}\]
Siis
\[A_n = \frac{2\pi^\frac{n+1}{2}}{\Gamma\left(\frac{n+1}{2}\right)}\,,\qquad A_{n-1} = \frac{2\pi^\frac{n}{2}}{\Gamma\left(\frac{n}{2}\right)}\,,\]
ja edelleen
\[V_n = \frac{A_{n-1}}{n} = \frac{2\pi^\frac{n}{2}}{n\,\Gamma\left(\frac{n}{2}\right)}\,.\]
\[V_n = \frac{2\pi^\frac{n}{2}}{n\,\Gamma\left(\frac{n}{2}\right)}\,,\qquad A_{n-1} = \frac{2\pi^\frac{n}{2}}{\Gamma\left(\frac{n}{2}\right)}\,. \]
Oheen on taulukoitu avaruuden \({\mathbb R}^n\) yksikköpallojen pinta-alat \(A_{n-1}\), yksikkökuulien tilavuudet \(V_n\) ja suhteet \(V_n/A_{n-1}\) dimensioissa \(n=1,\ldots,20\). Pallon pinta-ala on suurimmillaan, kun \(n=7\). Kuulan tilavuus on suurimmillaan, kun \(n=5\). Miettikääpä tätä! Onko edes järkevää vertailla eriulotteisia mittoja?
| \(n\) | \(A_{n-1}\) | \(V_n\) | \(V_n/A_{n-1}\) |
|---|---|---|---|
| 1 | 2,000000 | 2,000000 | 1,000000 |
| 2 | 6,283185 | 3,141593 | 0,500000 |
| 3 | 12,566371 | 4,188790 | 0,333333 |
| 4 | 19,739209 | 4,934802 | 0,250000 |
| 5 | 26,318945 | 5,263789 | 0,200000 |
| 6 | 31,006277 | 5,167713 | 0,166667 |
| 7 | 33,073362 | 4,724766 | 0,142857 |
| 8 | 32,469697 | 4,058712 | 0,125000 |
| 9 | 29,686580 | 3,298509 | 0,111111 |
| 10 | 25,501640 | 2,550164 | 0,100000 |
| 11 | 20,725143 | 1,884104 | 0,090909 |
| 12 | 16,023153 | 1,335263 | 0,083333 |
| 13 | 11,838174 | 0,910629 | 0,076923 |
| 14 | 8,389703 | 0,599265 | 0,071429 |
| 15 | 5,721649 | 0,381443 | 0,066667 |
| 16 | 3,765290 | 0,235331 | 0,062500 |
| 17 | 2,396679 | 0,140981 | 0,058824 |
| 18 | 1,478626 | 0,082146 | 0,055556 |
| 19 | 0,885810 | 0,046622 | 0,052632 |
| 20 | 0,516138 | 0,025807 | 0,050000 |
Kun \(n = 50\), on \(A_{n-1} \approx 8{,}651096\cdot10^{-12}\), \(V_n \approx 1{,}73021910^{-13}\) ja \(V_n/A_{n-1} = 0{,}02\).
Tehtävä 3. Osoita, että
\[\begin{split} &\text{(a)}\;\;\lim_{n\to\infty}A_{n-1}=0,\qquad \text{(b)}\;\;\lim_{n\to\infty}V_n=0,\\ &\text{(c)}\;\;\lim_{n\to\infty}\frac{V_n}{A_{n-1}}=0. \\ \end{split}\]
Onko tässä jotain outoa? Aikaisemminhan todettiin, että yksikköhyperkuution tilavuus on dimensiosta riippumatta aina 1, ja sen pinta-ala kasvaa rajatta, kun \(n\to\infty\)?
Tehtävä 4. Kertoma \(\{0,1,2,\ldots\}\to{\mathbb R}\), \(\ell\mapsto\ell\,!\), voitaisiin laajentaa funktioksi \([0,\infty[\to{\mathbb R}\), \(x\mapsto x!\), määrittelemällä
\[x! = \left\{\begin{array}{@{}c@{}c@{\phantom{x}}l} x\cdot(x-1)\cdot\ldots\cdot(x-k_x) &, & x>0, \\[1ex] 1 &, & x=0, \end{array}\right.\]
missä
\[k_x = \max\{\,k\in{\mathbb Z}\;|\;x-k>0\,\}.\]
Tutki funktion \(x\mapsto x!\) jatkuvuusominaisuuksia. Onko \(x!=\Gamma(x+1)\)?
Miksi solmut aukeavat?
Ohessa on kuva apilasolmusta (engl. trefoil knot). Siinä yksiulotteinen (joskin lihavoitu), näennäisesti kolmiulotteisessa avaruudessa kiemurteleva käyrä on projisoitu kaksiulotteiselle Solmu-lehden sivulle. Tuo lihava sulkeutuva käyrä todellakin näyttää solmulta meidän kolmiulotteiseen avaruuteen vangittujen kolmiulotteisten tarkkailijoiden näkökulmasta.


Neliulotteisessa avaruudessa vapaasti leijaileva tarkkailija tietää, että kyseessä ei ole solmu, vaikka sen projektio kolmiulotteiseen avaruuteen näyttää solmulta, ja projektio kaksiulotteiselle tasolle näyttää solmun kuvalta. Itse asiassa neljäs ulottuvuus on näkyvillä, se on koodattu käyrän väriin. Kuvassa on kolme näennäistä risteyskohtaa, jotka eivät oikeasti ole risteyskohtia edes kolmiulotteisessa avaruudessa. Neliulotteisessa avaruudessa “solmu” voidaan “aukaista” vetämällä ylimmän risteyskohdan taaempi eli tummempi käyränosa vaaleamman käyränosan eteen lähemmäksi katsojaa. Käyrä ei missään vetämisen vaiheessa leikkaa itseään silloinkaan, kun projektio kolmiulotteisessa avaruudessa näyttää leikkaavan itsensä, sillä käyrän neljäs koordinaatti \(x_4\) on erisuuri tummalla osuudella ja vaalealla osuudella. Oikealla on kuva “avatusta solmusta”. Kokeile tätä kotona! Saksien avulla saat tuntumaa neljänteen ulottuvuuteen.
Toinen vaihtoehto on vaan odotella. Minulla on pöydälläni apilasolmu rautalangasta taivuteltuna ja sulkeutuvaksi tinalla juotettuna. Juotos pitää, se ei ole kylmäjuotos! Joka aamu tarkastan solmun siltä varalta, että se olisi auennut. Aika nimittäin on suhteellisuusteorian neljäs ulottuvuus. Einsteinin mukaan emme olekaan kolmen ulottuvuuden vankeja, vaan liikumme alati neljännessä ulottuvuudessa, ja myös apilasolmu liikkuu. En hämmästyisi lainkaan, jos solmu jonain aamuna aukeaisi, kuin apilan lehti kasteisella niityllä, aamun ensi säteen sitä hellästi hipaistessa.
Viitteet
[1] Wikipedia: Gamma function.
https://en.wikipedia.org/wiki/Gamma_function
[2] Wikipedia: Hypercube.
https://en.wikipedia.org/wiki/Hypercube
[3] Wikipedia: Hyperplane.
https://en.wikipedia.org/wiki/Hyperplane
[4] Wikipedia: Knot theory.
https://en.wikipedia.org/wiki/Knot_theory
[5] Wikipedia: \(n\)-sphere.
https://en.wikipedia.org/wiki/N-sphere