Solmun 3/2022 tehtävien 1–10 ratkaisut
1. Osoita, että jos reaaliluvut \(x\), \(y\) ja \(z\) toteuttavat yhtälön
\[\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1,\]
niin
\[\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}=0.\]
Määritä jotkin ehdon toteuttavat reaaliluvut.
Ratkaisu. Oletetaan ensin, että \(x+y+z=0\), jolloin \(x+y=-z\), \(x+z=-y\) ja \(y+z=-z\). Tällöin osoitettavan tuloksen ehto on
\[1=\frac{x}{-x}+\frac{y}{-y}+\frac{z}{-z}=-1-1-1=-3,\]
mikä ei ole mahdollista. Näin ollen voidaan olettaa, että \(x+y+z\neq 0\).
Kun osoitettavan tuloksen ehdon yhtälö
\[\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1\]
kerrotaan nyt puolittain luvulla \(x+y+z\), niin saadaan ekvivalentti yhtälö
\[\begin{align*} &x+y+z\\ &=\frac{x^2+x(y+z)}{y+z}+\frac{y^2+y(x+z)}{x+z}+\frac{z^2+z(x+y)}{x+y}\\ &=\frac{x^2}{y+z}+x+\frac{y^2}{x+z}+y+\frac{z^2}{x+y}+z. \end{align*}\]
Näin ollen
\[\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}=0,\]
mikä pitikin osoittaa.
Olkoon esimerkiksi \(z=1\) ja \(x+y=-\frac{1}{5}\), jolloin \(y=-\frac{1}{5}-x\). Tällöin
\[\frac{x}{\frac{4}{5}-x}+\frac{-\frac{1}{5}-x}{1+x}+\frac{1}{-\frac{1}{5}}=1,\]
josta saadaan
\[50x^2+10x-31=0\iff x=\frac{-1\pm\sqrt{63}}{10}.\]
Valitaan näistä suurempi, jolloin saadaan
\[y=-\frac{1}{5}-x=\frac{-1-\sqrt{63}}{10}.\]
Näin ollen on löydetty yksi ehdon toteuttava kolmikko
\[\begin{cases} x=\dfrac{-1+\sqrt{63}}{10},\\ y=\dfrac{-1-\sqrt{63}}{10},\\ z=1. \end{cases}\]
2. Opri kirjoitti 2022 luvun listan seuraavasti: Listan kolmas luku on toinen luku jaettuna ensimmäisellä luvulla, listan neljäs luku on kolmas luku jaettuna toisella luvulla, ja niin edelleen, esimerkiksi listan 100. luku on 99. luku jaettuna 98. luvulla. Mikä on Oprin listan viimeinen luku, jos sen ensimmäinen luku on 20 ja toinen luku on 22?
Ratkaisu. Oprin listan kolmas luku on \(\frac{22}{20}=\frac{11}{10}\), neljäs luku on \(\frac{11}{10}:22=\frac{1}{20}\), viides luku on \(\frac{1}{20}:\frac{11}{10}=\frac{1}{22}\), kuudes luku on \(\frac{1}{22}:\frac{1}{20}=\frac{10}{11}\), seitsemäs luku on \(\frac{10}{11}:\frac{1}{22}=20\) ja kahdeksas luku on \(20:\frac{10}{11}=22\). Nyt havaitaan, että seitsemäs luku on sama kuin listan ensimmäinen luku ja kahdeksas luku on sama kuin listan toinen luku. Näin ollen listan luvut toistuvat kuuden luvun jaksoissa. Koska \(2022=6\cdot 337\), niin listan 2022. luku on ensimmäisestä luvusta lähtien kuuden luvun jakson viimeinen luku eli \(\frac{10}{11}\).
3. Nelikulmion \(ABCD\) sivut \(AD\) ja \(DC\) ovat yhtä pitkät. Kulman \(DAB\) suuruus on \(\alpha\), kulman \(ABC\) suuruus on \(2\alpha\), kulman \(BCD\) suuruus on \(3\alpha\) ja kulman \(CDA\) suuruus on \(4\alpha\). Osoita, että sivu \(AB\) on kaksi kertaa niin pitkä kuin sivu \(AD\).
Ratkaisu. Koska \(\alpha+2\alpha+3\alpha+4\alpha=10\alpha=360^\circ\), niin \(\alpha=36^\circ\). Näin ollen nelikulmion kulmien suuruudet ovat \(36^\circ\), \(72^\circ\), \(108^\circ\) ja \(144^\circ\). Kulmien suuruuksia ei tarvita tehtävän ratkaisussa, mutta ne auttavat alla olevan kuvan hahmottelemisessa.
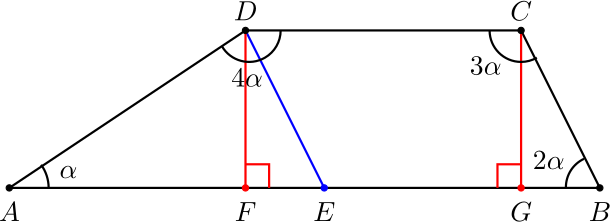
Koska \(5\alpha=180^\circ\), niin sivuille \(BC\) ja \(AD\) rajoittuvien nelikulmion kahden kulman summa on kummassakin tapauksessa \(180^\circ\). Tästä seuraa, että nelikulmion sivut \(AB\) ja \(DC\) ovat yhdensuuntaiset. Tämän voi perustella esim. piirtämällä pisteistä \(D\) ja \(C\) sivua \(AB\) vastaan kohtisuorat janat \(DF\) ja \(CG\), ks. kuva. Tällöin päätyihin syntyneitä suorakulmaisia kolmioita \(AFD\) ja \(BGC\) tarkastelemalla nähdään, että janat \(CG\) ja \(DF\) ovat kohtisuorassa myös sivua \(DC\) vastaan.
Näin ollen nelikulmio \(ABCD\) on puolisuunnikas. Sijoitetaan piste \(E\) sivulle \(AB\) niin, että sivut \(BC\) ja \(ED\) ovat yhdensuuntaiset. Tällöin nelikulmio \(BCDE\) on suunnikas. Koska kulma \(\angle EBC=2\alpha\), niin myös \(\angle AED=2\alpha\) ja \(\angle CDE=2\alpha\). Näin ollen \(\angle ADE=4\alpha-2\alpha=2\alpha\). Tästä seuraa, että \(AD=AE\). Koska \(BCDE\) on suunnikas, niin \(EB=DC\). Tehtävänannon mukaan \(AD=DC\), joten \(AE=AD=DC=EB\). Näin ollen \(AB=AE+EB=2AD\).
4. Olkoot \(x_1\) ja \(x_2\) yhtälön \(15x^2-21x+7=0\) reaalijuuret. Määritä lausekkeen
\[\frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{1}{x_1}+\frac{1}{x_2}\]
tarkka arvo.
Ratkaisu. Toisen asteen yhtälön diskriminantti on
\[(-21)^2-4\cdot 15\cdot 7 =21,\]
joten yhtälöllä on kaksi eri suurta reaalijuurta. Koska yhtälön vasemmalla puolella oleva vakio ei ole nolla, niin kumpikaan juurista \(x_1\) ja \(x_2\) ei ole nolla. Näin ollen kaikki määritettävässä lausekkeessa olevat murtoluvut on määritelty. Lasketaan juurten summa ja tulo Viéten kaavoilla:
\[x_1+x_2=\frac{21}{15}=\frac{7}{5},\quad x_1\cdot x_2=\frac{7}{15}.\]
Saadaan
\[\begin{align*} &\frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{1}{x_1}+\frac{1}{x_2} =\frac{x_1^2+x_2^2+x_1+x_2}{x_1x_2}\\ &=\frac{(x_1+x_2)^2-2x_1x_2+x_1+x_2}{x_1x_2}\\ &=\frac{(x_1+x_2)(x_1+x_2+1)}{x_1x_2}- 2\\ &=\frac{\frac{7}{5}\cdot\frac{12}{5}}{\frac{7}{15}}-2 =\frac{36}{5}-\frac{10}{5}=\frac{26}{5}. \end{align*}\]
5. Viisikulmion kaikki sivut ovat yhtä pitkiä ja kaksi sen kulmista ovat suoria. Kuinka suuria muut kolme kulmaa voivat olla?
Ratkaisu. Merkitään viisikulmion sivujen pituutta \(a\):lla ja sen kulmia \(A\), \(B\), \(C\), \(D\) ja \(E\), jolloin tarkasteltava viisikulmio on \(ABCDE\). Alla olevassa kuvassa on kaksi mahdollista tapausta, jossa viisikulmion suorat kulmat ovat vierekkäin kulmissa \(A\) ja \(B\).
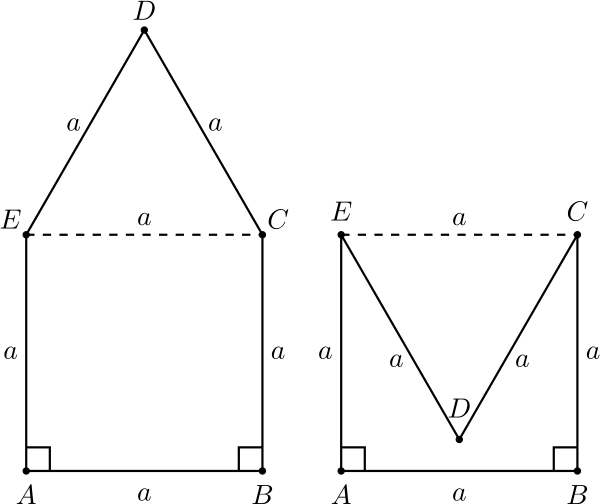
Molemmissa tapauksissa \(ABCE\) on neliö, joten \(EC=a\). Näin ollen kolmio \(CDE\) on tasasivuinen ja sen kulmien suuruus on \(60^\circ\). Vasemmanpuoleisessa viisikulmiossa \(ABCDE\) tuntemattomien kulmien suuruudet ovat \(\angle CDE=60^\circ\) ja \(\angle BCD=\angle DEA=90^\circ+60^\circ=150^\circ\). Oikeanpuoleisessa viisikulmiossa \(ABCDE\) huomataan, että \(\angle BCD=\angle AED=90^\circ-60^\circ=30^\circ\). Lisäksi viides tuntematon kulma on \(\angle CDE=360^\circ-60^\circ=300^\circ\).
Tasasivuinen viisikulmio \(ABCDE\) voidaan muodostaa myös niin, että suorat kulmat eivät ole vierekkäin, kuten seuraavassa kuvassa on esitetty.
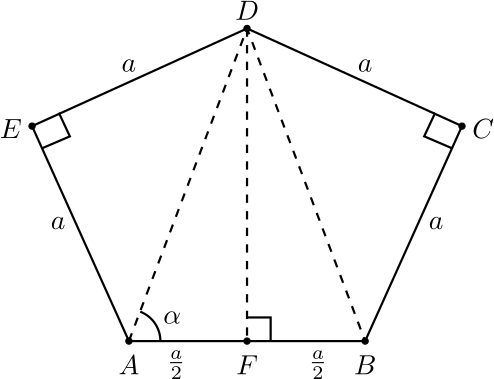
Kolmiot \(ADE\) ja \(BCD\) ovat tasakylkisiä ja suorakulmaisia, joten \(AD=BD=a\sqrt{2}\) ja \(\angle DAE=\angle ADE=\angle DBC=\angle BDC=45^\circ\). Merkitään \(\alpha=\angle BAD=\angle ABD\). Tällöin
\[\cos\alpha=\frac{AF}{AD}=\frac{\frac{a}{2}}{a\sqrt{2}}=\frac{1}{2\sqrt{2}},\]
joten \(\alpha\approx 69{,}295^\circ\) ja \(\angle ADF=90^\circ-\alpha=20{,}705^\circ\). Näin ollen tuntemattomien kulmien suuruuksiksi saadaan \(\angle BAD=\angle ABC=45^\circ+\alpha\approx 114{,}295^\circ\) ja \(\angle CDE=2\cdot 45^\circ+2\cdot\angle ADF\approx 131{,}410^\circ\).
Kaikissa edellä esitetyissä kolmessa tapauksessa on helppo tarkistaa, että viisikulmion kulmien summa on \(540^\circ\), kuten pitääkin olla. Muita mahdollisia tapauksia ei ole, koska suorat kulmat ovat joko vierekkäisissä kulmissa tai niin, että niiden välissä on yksi kulma, jolloin toiseen suuntaan välissä on kaksi kulmaa.
6. Edel tekee puisia tikkuja, joiden pituus on kokonaisluku. Mitkään kolme tikkua eivät saa muodostaa kolmiota. Tikuissa on pituudeltaan 1 ja 10 olevat tikut ja pisimmän tikun pituus on 100. Kuinka monta tikkua Edel voi enintään tehdä?
Ratkaisu. Jotta kolmesta tikusta ei voi muodostaa kolmiota, on pisimmän tikun pituuden oltava vähintään kahden lyhemmän tikun pituuden summa. Näin ollen tikkuja saataisiin eniten, jos niiden pituudet olisivat 1, 1, 2, 3, 5, 8, 13, 21,…Koska yhden tikun pituuden on kuitenkin oltava 10, niin pituudeltaan 8 oleva tikku on korvattava tikulla, jonka pituus on 10, sillä \(3+5<10<5+8\). Näin ollen tikkujen pituudet voisivat olla 1, 1, 2, 3, 5, 10, 15, 25, 40, 65, 105,…Koska pisimmän tikun pituuden on oltava 100, niin pituudeltaan 65 oleva tikku on korvattava tikulla, jonka pituus on 100, sillä \(25+40<100<40+65\). Tikkujen pituudet voivat siis olla 1, 1, 2, 3, 5, 10, 15, 25, 40, 100, ja Edel voi näin ollen tehdä enintään 10 tikkua.
7. Kahden kolminumeroisen luvun keskiarvo on luku, joka saadaan kirjoittamalla kyseiset luvut peräkkäin ja erottaen luvut desimaalipilkulla. Mitkä nämä kaksi lukua ovat?
Ratkaisu. Olkoot \(A\) ja \(B\) etsityt kolminumeroiset luvut ja merkitään ne peräkkäin kirjoitettuna ja desimaalipilkulla erotettuna \(\overline{A,\!B}\). Tällöin
\[\frac{A+B}{2}=\overline{A{,}B}=A+\frac{B}{1000},\]
joten
\[A+B=2A+\frac{B}{500}.\]
Koska \(A+B\) ja \(2A\) ovat kokonaislukuja, niin myös luvun \(\frac{B}{500}\) on oltava kokonaisluku. Mutta koska \(B\) on kolminumeroinen, niin ainoa mahdollisuus on, että \(B=500\). Tällöin \(A=B-1=500-1=499\). Voidaan vielä tarkistaa, että
\[\frac{499+500}{2}=\frac{999}{2}=499{,}500.\]
8. Yksikköneliön sisään piirretään neljä ympyrää kuten alla olevassa kuvassa on esitetty. Kaksi suurempaa ympyrää ovat samankokoiset ja samoin kaksi pienempää ympyrää ovat samankokoiset. Ympyrät sivuavat toisiaan ja neliön sivuja. Mikä on ympyröiden keskipisteet yhdistämällä muodostuvan vinoneliön pinta-ala?

Ratkaisu. Tarkastellaan alla olevassa kuvassa esitettyä tilannetta, jossa suurempien ympyröiden säde on \(R\) ja pienempien ympyröiden säde on \(r\). Tehtävänannon perusteella \(CD=CL+LM+MD=1\).
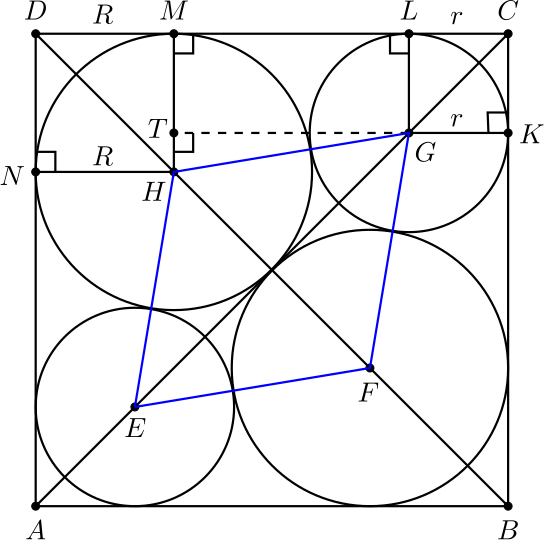
Nelikulmio \(CLGK\) on neliö, jonka sivun pituus on \(r\), ja nelikulmio \(DNHM\) on neliö, jonka sivun pituus on \(R\). Nyt \(HT=R-r\) ja \(GH=r+R\), sillä janassa \(GH\) on pienen ja ison ympyrän säteet peräkkäin. Suorakulmaisesta kolmiosta \(GTH\) saadaan
\[(R+r)^2=GT^2+(R-r)^2,\]
joten \(GT^2=4Rr\). Näin ollen \(LM=GT=2\sqrt{Rr}\) ja saadaan
\[1=r+LM+R=r+2\sqrt{Rr}+R=(\sqrt{r}+\sqrt{R})^2.\]
Koska \(\sqrt{r}+\sqrt{R}>0\), niin \(\sqrt{r}+\sqrt{R}=1\).
Lasketaan ensin säde \(R\). Koska \(BD=\sqrt{2}\), \(BF=DH=\sqrt{2}R\) ja \(FH=2R\), niin
\[2R+2\sqrt{2}R=\sqrt{2}\]
ja näin ollen
\[R=\frac{1}{2+\sqrt{2}}=1-\frac{\sqrt{2}}{2}.\]
Nyt
\[\sqrt{r}=1-\sqrt{R}=1-\sqrt{1-\frac{\sqrt{2}}{2}},\]
joten neliöön korottamalla saadaan
\[r=1-2\sqrt{1-\frac{\sqrt{2}}{2}}+1-\frac{\sqrt{2}}{2} =2-\frac{\sqrt{2}}{2}-\sqrt{4-2\sqrt{2}}.\]
Huomataan, että suunnikkaan \(EFGH\) lävistäjien pituudet ovat \(FH=2R\) ja \(EG=\sqrt{2}-2\sqrt{2}r\). Koska lävistäjät ovat kohtisuorassa toisiaan vasten, niin suunnikkaan pinta-ala saadaan kaavalla
\[\begin{align*} \text{ala}&=\frac{FH\cdot EG}{2}=\frac{2R(\sqrt{2}-2\sqrt{2}r)}{2} =R(\sqrt{2}-2\sqrt{2}r)\\ &=\left(\!1-\frac{\sqrt{2}}{2}\right)\!\left(\!\sqrt{2}-2\sqrt{2} \left(\!2-\frac{\sqrt{2}}{2}-\sqrt{4-2\sqrt{2}}\right)\!\right)\\ &=5-4\sqrt{2}+2\sqrt{(2-\sqrt{2})^3} \approx 0{,}2398. \end{align*}\]
9. Määritä kaikki positiiviset reaaliluvut \(x\), joille \(x+\frac{1}{x}\) on kokonaisluku ja \(x^3+\frac{1}{x^3}\) on alkuluku.
Ratkaisu. Kun \(x+\frac{1}{x}=n\) on positiivinen kokonaisluku, niin myös sen neliö
\[\left(x+\dfrac{1}{x}\right)^2=x^2+\frac{1}{x^2}+2=n^2\]
on positiivinen kokonaisluku. Edelleen
\[x^2+\frac{1}{x^2}=n^2-2\]
on positiivinen kokonaisluku, joten \(n>1\). Kertomalla nyt yhtälöt
\[x+\dfrac{1}{x}=n\quad\text{ja}\quad x^2+\frac{1}{x^2}=n^2-2\]
puolittain keskenään saadaan
\[x^3+\frac{1}{x^3}+x+\frac{1}{x}=n^3-2n,\]
joten
\[x^3+\frac{1}{x^3}=n^3-3n=n(n^2-3),\]
joka on kahden positiivisen kokonaisluvun tulo. Se on alkuluku täsmälleen silloin, kun toinen tekijä on \(1\) ja toinen on alkuluku. Koska \(n>1\), niin on oltava \(n^2-3=1\) eli \(n=2\). Näin ollen \(x+\frac{1}{x}=2\), joten \(x=1\).
10. Mitkä luvuista \(1,\ldots,50\) voidaan lausua vähintään kahden peräkkäisen ei-negatiivisen kokonaisluvun summana?
Ratkaisu. Kaikki parittomat positiiviset kokonaisluvut voidaan esittää kahden peräkkäisen ei-negatiivisen kokonaisluvun summana. Pariton luku jaettuna kahdella ei ole kokonaisluku, mutta kun lasketaan osamäärää edellinen ja seuraava kokonaisluku yhteen, saadaan tarkasteltavana oleva pariton luku:
\[1=0+1,\ 3=1+2,\ 5=2+3,\ldots,\ 49=24+25.\]
Toisaalta positiivisia parillisia lukuja ei voida esittää kahden peräkkäisen kokonaisluvun summana, koska kahden peräkkäisen kokonaisluvun summa on aina pariton luku.
Tarkastellaan seuraavaksi positiivisia parillisia kokonaislukuja, joissa on tekijänä pariton positiivinen kokonaisluku \(n\neq 1\). Tällöin tarkasteltava luku voidaan esittää tulona \(m\cdot n\), missä \(m\) on positiivinen kokonaisluku. Asetetaan luvun toinen tekijä \(m\) summan keskimmäiseksi yhteenlaskettavaksi ja lisätään siihen vuorotellen \(m\):ää pienempiä ja suurempia peräkkäisiä kokonaislukuja niin monta, että summaan tulee yhteensä \(n\) yhteenlaskettavaa lukua. Tällöin summaksi saadaan tarkasteltava luku. Esimerkiksi
\[42=7\cdot 6=3+4+5+6+7+8+9.\]
Huomataan, että koska \(m\):ää pienempiä lukuja lisätään summaan \(\frac{m-1}{2}\) kappaletta, niin kaikki summan luvut ovat positiivisia. Tällöin siis löydetään aina summaan vaadittavat peräkkäiset ei-negatiiviset kokonaisluvut.
Tarkastellaan sitten positiivisia parillisia kokonaislukuja, joilla ei ole tekijänä paritonta positiivista kokonaislukua \(n\neq 1\). Tällöin kaikki tekijät ovat parillisia lukuja, jotka ovat luvun \(2\) potensseja \(2^k\), \(k\in\mathbb{N}\). Tällaisia lukuja ei ole mahdollista esittää enemmän kuin kahden peräkkäisen kokonaisluvun summana.
Perustellaan tämä tekemällä vastaoletus, että vähintään kolmen peräkkäisen kokonaisluvun summa on \(2^k\). Oletetaan ensin, että yhteenlaskettavia lukuja on pariton määrä \(n\). Tällöin summan keskimmäinen luku on yhteenlaskettavien lukujen keskiarvo, joten \(n\) on luvun \(2^k\) tekijä. Tämä on ristiriita, koska luvulla \(2^k\) on vain parillisia tekijöitä luvun \(1\) lisäksi.
Oletetaan sitten, että yhteenlaskettavia lukuja on parillinen määrä \(2n\). Tällöin yhteenlaskettavien lukujen keskiarvo ei ole kokonaisluku vaan “puoliluku” \(m+0{,}5\), \(m\in\mathbb{N}\), jolloin
\[(m+0{,}5)\cdot 2n =2^k\quad\text{eli}\quad (2m+1)\cdot 2n=2^{k+1}.\]
Tämä on ristiriita, koska luku \(2m+1\) on pariton, mutta luvulla \(2^{k+1}\) ei ole parittomia tekijöitä.
Näin ollen lukuja \(2\), \(4\), \(8\), \(16\) ja \(32\) ei voida esittää vähintään kahden peräkkäisen ei-negatiivisen kokonaisluvun summana, mutta kaikki muut \(45\) lukua väliltä \(1,\ldots,50\) voidaan esittää.
Solmun 3/2022 tehtävien 11–20 ratkaisut julkaistaan seuraavassa numerossa.
Lähde: KöMaL
Käännös ja sovitus suomeksi: Mika Koskenoja