Harmonisesta keskiarvosta
Pekka Smolander
Karelia-ammattikorkeakoulu
Luvuille voidaan tavallisen keskiarvon eli aritmeettisen keskiarvon lisäksi määritellä myös muita keskiarvoja, esimerkiksi geometrinen keskiarvo ja harmoninen keskiarvo. Muistutetaan mieleen, että positiivisten lukujen \(a\) ja \(b\) aritmeettinen keskiarvo on
\[A=\frac{a+b}{2}\]
ja geometrinen keskiarvo
\[G=\sqrt{ab}.\]
Harmoninen keskiarvo voidaan määritellä käänteislukujen avulla seuraavalla ilmaisulla: “Lukujen \(a\) ja \(b\) harmoninen keskiarvo \(H\) on käänteislukujen \(1/a\) ja \(1/b\) aritmeettisen keskiarvon käänteisluku.” Tämä ajatus ilmaistaan kaavalla
\[\frac{1}{H}=\frac{1/a+1/b}{2},\]
tai
\[\frac{2}{H}=\frac{1}{a}+\frac{1}{b}.\]
Ratkaisemalla tästä \(H\) saadaan, että lukujen \(a\) ja \(b\) harmoninen keskiarvo on
\[H=\frac{2ab}{a+b}.\]
Tarkastelemalla kaavoja nähdään, että nämä kolme keskiarvoa liittyvät läheisesti toisiinsa. Nimittäin positiivisille luvuille \(a\) ja \(b\) saadaan
\[AH=\frac{a+b}{2}\cdot \frac{2ab}{a+b} =ab=G^2.\]
Näin ollen
\[G=\sqrt{AH},\]
eli \(G\) on lukujen \(A\) ja \(H\) geometrinen keskiarvo.
Tässä kirjoitelmassa ollaan kiinnostuneita harmonisesta keskiarvosta. Katsotaan ensin, kuinka se liittyy keskinopeuksien laskemiseen ja värähtelevän kielen äänenkorkeuksiin. Lopuksi käsitellään muutamia harmonisen keskiarvon geometrisia konstruktioita.
Yksi harmonisen keskiarvon konstruktio on esitelty Solmun artikkelissa [1]. Siinä konstruoidaan useita kahden luvun eri keskiarvoja puolisuunnikkaan avulla. Nettihaku “harmonic mean” johtaa verkkosivuille, joilta löytyy lisää harmonisen keskiarvon konstruktioita. Katso esimerkiksi [2].
Nopeuksien keskiarvo
Tarkastellaan seuraavaa ajatusleikkiä. Pekka ajaa polkupyörällä ensin 5 km nopeudella 10 km/h ja sen jälkeen 5 km nopeudella 30 km/h. Mikä on Pekan keskinopeus koko 10 km pyörälenkillä?
Ensiksi tulee mieleen nopeus 20 km/h, sillä 20 on lukujen 10 ja 30 keskiarvo. Tällä nopeudella Pekalta kuluisi 10 km:n matkaan puoli tuntia. Mutta Pekalta kuluu nopeudella 10 km/h jo pyörälenkin 5 km:n alkumatkaan puoli tuntia. Siis keskinopeus ei voi olla 20 km/h. Luovutaan kokeilemisesta.
Oikea keskinopeus saadaan, kun lasketaan ensin matkaan käytetty aika ja jaetaan sillä matka 10 km. Kuten jo edellä huomattiin 5 km:n matkaan nopeudella 10 km/h aikaa kuluu 30 min. Vastaavasti 5 km:n loppumatkaan nopeudella 30 km/h aikaa kuluu 10 min. Koko 10 km pyörälenkkiin kuluu siis aikaa 40 min, josta saadaan keskinopeudeksi 15 km/h.
Mutta kuinka luku 15 liittyy lukuihin 10 ja 30? Lasketaan keskinopeus yleisemmässä tilanteessa. Ajatellaan, että ensin ajetaan matka \(s\) keskinopeudella \(v_1\) ja sen jälkeen sama matka \(s\) keskinopeudella \(v_2\). Näihin matkoihin käytetään ajat \(t_1=s/v_1\) ja \(t_2=s/v_2\). Siis keskinopeus koko matkalla on
\[v=\frac{2s}{t_1+t_2}\ ,\]
josta muokkauksen jälkeen saadaan
\[v=\frac{2v_1v_2}{v_1+v_2}.\]
Siis \(v\) on lukujen \(v_1\) ja \(v_2\) harmoninen keskiarvo. Nyt jos \(v_1=10\) ja \(v_2=30\), niin
\[v=\frac{2\cdot 10\cdot30}{10+30}=15.\]
Duurikolmisointu
Nimitykset harmoninen keskiarvo ja harmoninen jono periytyvät antiikin Kreikasta, jossa Pythagoraan koulukunta teki huomioita värähtelevien kielten pituuksien ja sävelkorkeuksien yhteydestä. Huomattiin, että jos kolmen samanlaisen kielen pituudet suhtautuvat toisiinsa kuten luvut 1/4, 1/5 ja 1/6, niin saadaan harmoniselta kuulostava sointu. Näin muodostuukin puhdas duurikolmisointu. Katsotaan, kuinka se liittyy harmoniseen keskiarvoon.
Tarkastellaan värähtelevää kieltä ja merkitään vapaan kielen pituutta luvulla 1. Tehdään seuraavia huomioita:
Jos kieli laitetaan värähtelemään ensin koko pituudella 1 ja sitten pituudella 1/2, niin äänien taajuudet muodostavat oktaavin suuruisen intervallin.
Lukujen 1 ja 1/2 harmoninen keskiarvo on 2/3. Kielen pituuksia \(1\) ja 2/3 vastaavien äänien taajuudet muodostavat intervallin puhdas kvintti.
Lukujen 1 ja 2/3 harmoninen keskiarvo on 4/5 ja kielen pituuksia 1 ja 4/5 vastaavista äänien taajuuksista syntyy intervalli suuri terssi.
Näin ollen värähdyspituuksia 1, 4/5 ja 2/3 vastaavista taajuuksista muodostuu duurikolmisointu.
Huomataan, että duurisoinnun antavat kielen värähtelypituudet 1, 4/5 ja 2/3 suhtautuvat toisiinsa samalla tavalla kuin luvut 1/4, 1/5 ja 1/6. Kannattaa huomata myös, että tässä puhutaan puhtaista intervalleista. Soitinten tasaviritys ei aivan täsmälleen tuota tässä tarkasteltuja kielen pituuksien suhteita.
Konstruktio
Kahden positiivisen luvun harmoniselle keskiarvolle on keksitty useita erilaisia konstruktioita. Solmun artikkelissa [1] esitetään yksi konstruktio puolisuunnikkaan avulla. Piirtämällä puolisuunnikas sopivasti voidaan tuota päättelyä hieman keventää.
Olkoot \(a\) ja \(b\) positiivisia lukuja. Piirretään janat \(AB\) ja \(CD\) siten, että \(a=AB\) ja \(b=CD\) ja että nämä janat ovat kohtisuorassa janan \(AC\) kanssa. Piirretään yhdysjanat \(AD\) ja \(BC\). Olkoon \(E\) yhdysjanojen leikkauspiste ja \(F\) pisteen \(E\) kohtisuora projektio janalle \(AC\). Merkitään \(c=EF\) ja osoitetaan, että \(c\) on lukujen \(a\) ja \(b\) harmonisen keskiarvon puolikas.
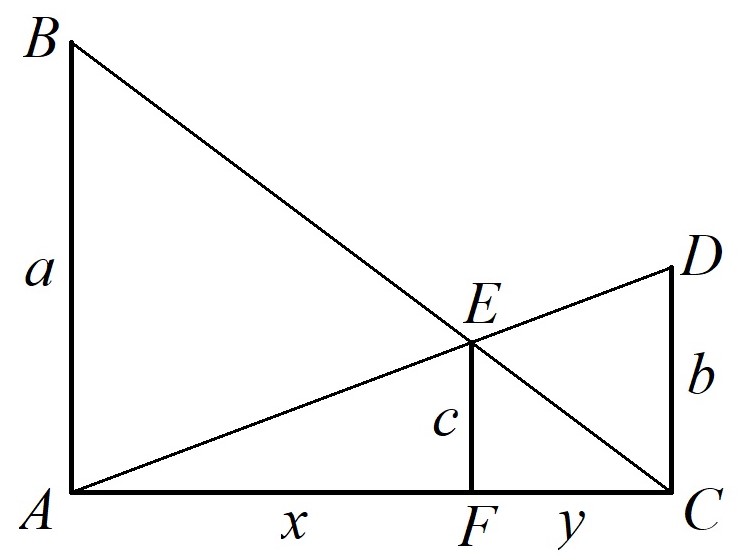
Merkitään \(x=AF\) ja \(y=CF\). Kolmioiden \(ABC\) ja \(FEC\) yhdenmuotoisuuden perusteella
\[\frac{x+y}{y}=\frac{a}{c}\]
eli
\[\frac{x}{y}+1=\frac{a}{c}.\]
Koska \(x\) ja \(y\) ovat yhdenmuotoisten kolmioiden \(ABE\) ja \(CDE\) korkeudet, niin niille pätee
\[\frac{x}{y}=\frac{a}{b}.\]
Siis
\[\frac{a}{b}+1=\frac{a}{c}.\]
Ratkaisemalla tästä \(c\) saadaan
\[c=\frac{ab}{a+b}.\]
Siis \(c\) on puolet lukujen \(a\) ja \(b\) harmonisesta keskiarvosta.
Virtaviivaistetaan konstruktiota
Edellisessä konstruktiossa käytettiin verrantoa
\[\frac{x}{y}=\frac{a}{b}.\]
Koska \(x+y\) on janan \(AC\) pituus, se voidaan valita vapaasti. Valitaan nyt \(x=a\) ja \(y=b\). Tällöin riittää tarkastella edellisen kuvan kolmiota \(ACD\), joka on irrotettu oheiseen kuvaan.
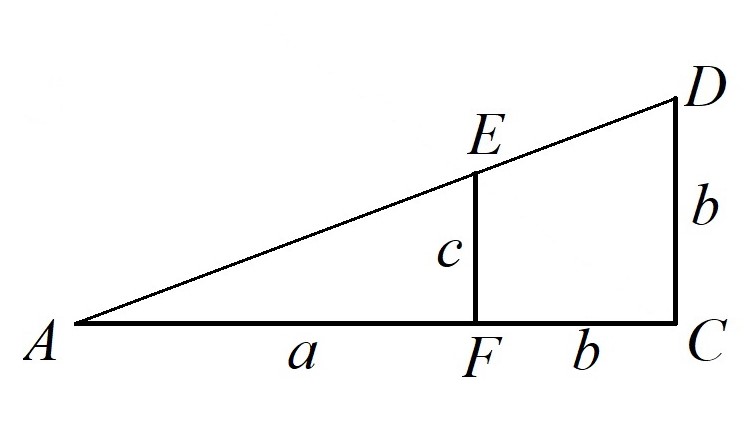
Muodostetaan siis suorakulmainen kolmio \(ACD\), jolla on kateetit \(a+b=AC\) ja \(b=CD\). Valitaan sivulta \(AC\) sellainen piste \(F\), että \(a=AF\) ja \(b=FC\). Valitaan sivulta \(AD\) piste \(E\) siten, että \(FE\) on yhdensuuntainen sivun \(CD\) kanssa.
Merkitään \(c=EF\). Nyt nähdään, että \(c\) on puolet lukujen \(a\) ja \(b\) harmonisesta keskiarvosta. Nimittäin kolmiot \(AFE\) ja \(ACD\) ovat yhdenmuotoisia, joten
\[\frac{c}{b}=\frac{a}{a+b}.\]
Siis
\[c=\frac{ab}{a+b}.\]
Tehtäviä
Aiheesta kiinnostunut lukija voi konstruoida positiivisten lukujen \(a\) ja \(b\) harmonisen keskiarvon puolikkaan seuraavien tehtävien avulla. Konstruktioiden todistukset ovat mukavia geometrian harjoitustehtäviä ja ne jätetään lukijalle.
Tehtävä 1. Piirretään kolmio \(OAB\) siten, että \(a=OA\) ja \(b=OB\). Lisäksi oletetaan, että kulma \(AOB\) on 120 astetta. Olkoon \(C\) kulman \(AOB\) puolittajan ja sivun \(AB\) leikkauspiste.
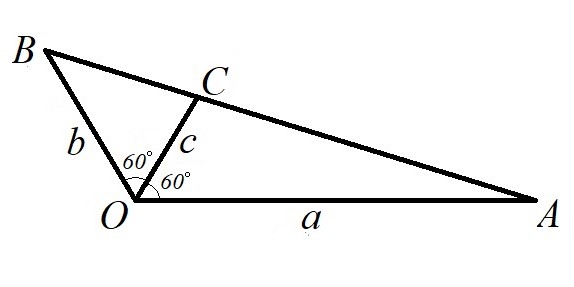
Osoita, että luvulle \(c=OC\) pätee
\[\frac{1}{c}=\frac{1}{a}+\frac{1}{b}.\]
Tehtävä 2. Piirretään kolmio \(OAB\) siten, että \(a=OA\) ja \(b=OB\). Olkoon \(C\) kulman \(AOB\) puolittajan ja sivun \(AB\) leikkauspiste. Olkoon \(D\) sivun \(OB\) sellainen piste, että jana \(DC\) on yhdensuuntainen sivun \(OA\) kanssa.
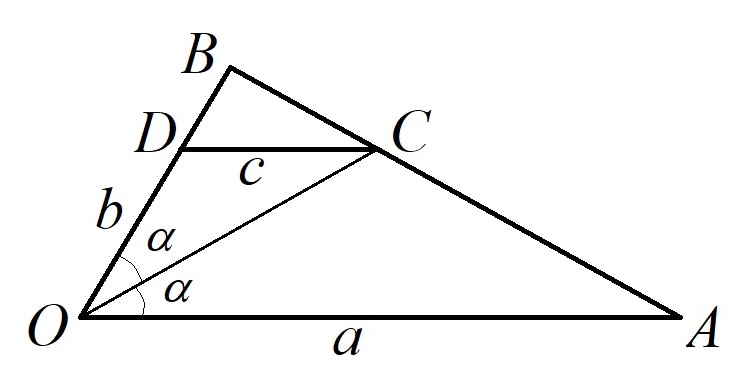
Osoita, että luvulle \(c=DC\) pätee
\[\frac{1}{c}=\frac{1}{a}+\frac{1}{b}.\]
Viitteet
[1] Esa V. Vesalainen: “Kahden muuttujan keskiarvoista”, Solmu 1/2019, s. 11-14.
https://matematiikkalehtisolmu.fi/2019/1/keskiarvoista.pdf