Euroopan tyttöjen matematiikkaolympialaisten 2022 tehtäviä ja ratkaisuja

Aino Aulanko, Siiri Roschier, Anni Tapionlinna, Minea Tiitinen

Tehtävä 1: Olkoon \(ABC\) teräväkulmainen kolmio, jossa on voimassa \(BC < AB\) ja \(BC <CA\). Olkoon \(P\) sellainen piste janalla \(AB\) ja \(Q\) sellainen piste janalla \(AC\), että \(P\ne B, Q\ne C\) ja \(BQ=BC=CP\). Olkoot \(T\) kolmion \(APQ\) ympäri piirretyn ympyrän keskipiste, \(H\) kolmion \(ABC\) ortokeskus ja \(S\) suorien \(BQ\) ja \(CP\) leikkauspiste. Osoita, että pisteet \(T\), \(H\) ja \(S\) ovat samalla suoralla.

Ratkaisu (Siiri): Todistus perustuu sen osoittamiseen, että sekä piste \(H\) että piste \(T\) ovat kulman \(\angle BSC\) kulmanpuolittajalla. Osoitetaan aluksi, että piste \(H\) on tällä kulmanpuolittajalla. Koska \(BQ=BC=CP\), on kolmio \(\Delta BCP\) tasakylkinen, ja siten sen kulmasta \(C\) lähtevä korkeusjana on myös sen kulmanpuolittaja. Täten sen kulmanpuolittaja kulkee pisteen \(H\) kautta. Sama voidaan osoittaa identtisesti kolmiolle \(\Delta QBC\), ja saadaan, että kulmien \(\angle CBQ=\angle CBS\) ja \(\angle PCB=\angle SCB\) kulmanpuolittajat kulkevat pisteen \(H\) kautta. Koska kolmion kulmanpuolittajat leikkaavat kaikki samassa pisteessä, voidaan huomata myös kulman \(\angle BSC\) kulmanpuolittajan kulkevan pisteen \(H\) kautta.

Ristikulmina \(\angle BSC=\angle QSP\). Tasakylkisestä kolmiosta \(\Delta BCP\) saamme, että \(\angle PCB=\angle SCB=180^{\circ}-2\angle B\), ja vastaavasti kolmiosta \(\Delta QBC\) yhtäsuuruuden \(\angle CBQ=\angle CBS=180^{\circ}-2\angle C\). Tästä saamme

\[\begin{align*} \angle QSP &=\angle BSC=180^{\circ}-\angle SCB-\angle CBS\\ &=180^{\circ}-\left(180^{\circ}-2\angle B\right)-\left(180^{\circ}-2\angle C\right)\\ &=180^{\circ}-2\angle A. \end{align*}\]

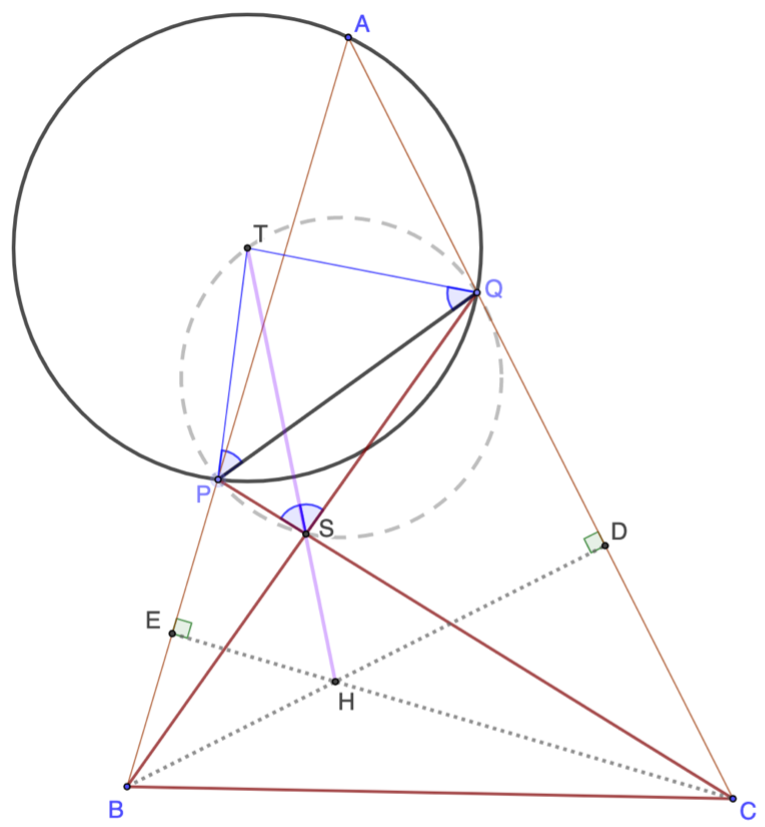
Koska \(T\) on ympyrän \(APQ\) keskipiste, \(\angle PTQ=2\angle PAQ=2\angle BAC=2\angle A\). Nyt \(\angle PTQ+\angle QSP=2\angle A+180^{\circ}-2\angle A=180^{\circ}\), ja \(PTQS\) on jännenelikulmio. Koska ympyrän säteinä \(PT=TQ\), ovat niiden kehäkulmatkin samat, \(\angle TSP=\angle TQP=\angle QPT=\angle QST\). Siis \(T\) on kulman \(\angle QSP\) kulmanpuolittajalla, joka on sama suora kuin ristikulman \(\angle BSC\) puolittaja, jolla \(H\) sijaitsi, ja voimme todeta, että pisteet \(T\), \(S\) ja \(H\) sijaitsevat kaikki samalla suoralla, joka on kulman \(\angle QSP\) kulmanpuolittaja.

Tehtävä 2: Olkoon \(N = \{ 1, 2, 3, \ldots \}\) positiivisten kokonaislukujen joukko. Etsi kaikki funktiot \(f \colon N \to N\), joille pätee kaikilla positiivisilla kokonaisluvuilla \(a\), \(b\)

\(f(ab) = f(a) f(b)\) sekä
ainakin kaksi luvuista \(f(a)\), \(f(b)\) ja \(f(a + b)\) ovat yhtäsuuria.

Ratkaisu (Anni): Vastaukseksi saadaan \(f(n) = k^{\nu_p(n)}\), jossa \(k \in N\), \(p\) on alkuluku ja \(\nu_p(n)\) on \(p\):n suurin potenssi, joka jakaa \(n\):n.

Ensiksi voimme todeta kaikkien tätä muotoa olevien funktioiden toteuttavan ehdot. Ensimmäinen ehto pätee, sillä

\[\begin{align*} f(ab) &= k^{\nu_p(ab)} = k^{\nu_p(a)+\nu_p(b)}\\ &= k^{\nu_p(a)} \cdot k^{\nu_p(b)} = f(a) f(b). \end{align*}\]

Toinen ehto pätee, sillä jos \(\nu_p(a) = \nu_p(b)\), niin selkeästi \(f(a) = f(b)\), ja jos \(\nu_p(a) \neq \nu_p(b)\), niin pätee \(\nu_p(a +b) = \min(\nu_p(a), \nu_p(a), \nu_p(b))\), jolloin \(f(a+b = f(a))\) tai \(f(a+b) = f(b)\).

Seuraavaksi osoitetaan näiden olevan ainoat ratkaisut. Sijoittamalla \(a = b = 1\) ensimmäiseen yhtälöön saadaan \(f(1) = 1\). Lisäksi yksinkertaisella induktiolla saadaan

\[f \big(\prod_{i=1}^k P_i^{\alpha_i}\big) = \prod_{i=1}^k f(p_i)^{\alpha_i}.\]

Olkoon \(S\) joukko alkulukuja \(p\), joilla \(f(p) \neq 1\). Jos \(|S| = 1\), niin \(S = \{ p \}\) ja \(f(p) = k\) jollain \(k \neq 1\), ja siksi aiemman induktion tuloksesta \(f(n) = K ^{\nu_p(n)}\). Toisaalta, jos \(S\) on tyhjä joukko, niin \(f(n) = 1\) kaikilla \(n,\) jonka voi kirjoittaa aiemmassa muodossa, kun \(k = 1\). Oletetaan nyt, että \(S\) sisältää vähintään kaksi alkulukua. Olkoot \(p < q\) joukon kaksi pienintä alkiota. Koska kaikki \(q-p\):n alkutekijät ovat \(q\):ta pienempiä ja erisuuria kuin \(p\), niin \(f(q-p) = 1\). Käyttäen ehtoa (2) lukuihin \(p\) ja \(q-p\) saadaan, että jotkin kaksi luvuista \(f(p= \neq 1\), \(f(q) \neq 1\), \(f(q-p) = 1\) ovat yhtäsuuria. Tästä seuraa, että \(f(p) = f(q)\). Olkoon \(t \geq 2\) pienin kokonaisluku, jolla \(p^t > q\), ja merkitään \(p^t = aq + b\), jossa \(0 \leq b < q\). Koska \(q \geq p^{t-1}\), eikä \(q\) ole jaollinen \(p\):llä, niin saamme \(q > p^{t-1}\), eli \(a < p\) ja siksi \(f(a) = 1\). Tästä seuraa, että \(aq\) ei ole jaollinen \(p\):llä eikä täten myöskään \(b\) ole. Koska \(b < q\), niin \(f(b) = 1\), nyt käyttäen toista ehtoa lukuihin \(aq\) ja \(b\) saamme, että jotkin kaksi luvuista \(f(aq) = f(a)f(q) = f(q) = f(p)\), \(f(b) = 1\) ja \(f(aq+b) = f(p^t) = f(p)^t\) ovat yhtäsuuria, mikä on ristiriita, joten joukko \(S\) sisältää joko yhden tai ei yhtäkään alkulukua, jolloin ainoa ratkaisu on \(f(n) = k^{\nu_p(n)}\).

Tehtävä 4: On annettu positiivinen kokonaisluku \(n \geq2\), selvitä suurin positiivinen kokonaisluku \(N\), jota kohti on olemassa \(N+1\) reaalilukua \(a_0\), \(a_1, \ldots, a_N\), joilla

\(a_0+a_1=-\frac{1}{n}\) ja
\((a_k+a_{k-1})(a_k+a_{k+1})=a_{k-1}-a_{k+1}\), kun \(1 \leq k \leq N-1\).

Ratkaisu (Aino): Kerron tässä oman ratkaisuni sekä sen, minkä ideoiden kautta päädyin siihen.

Kokeilin ensin, mitä tapahtuu, jos \(n=2\). Nyt valitaan \(k=1\), saadaan yhtälö

\[\begin{align*} (a_1+a_0)(a_1+a_2)&=a_0-a_2\\ -\frac{1}{2}(a_1+a_2)&=a_0-a_2\\ -\frac{1}{2} a_1-a_0+\frac{1}{2} a_2&=0\\ -\frac{1}{2}(a_1+a_0)-\frac{1}{2}(a_0-a_2)&=0\\ -\frac{1}{2}(a_0-a_2)&=-\frac{1}{4}\\ a_0-a_2&=\frac{1}{2}. \end{align*}\]

Sijoitetaan tämä alkuperäiseen yhtälöön ja saadaan

\[\begin{align*} -\frac{1}{2}(a_1+a_2)&=\frac{1}{2}\\ a_1+a_2&=-1. \end{align*}\]

Nyt valitaan \(k=2\):

\[\begin{align*} (a_2+a_1)(a_2+a_3)&=a_1-a_3\\ -a_2-a_3&=a_1-a_3\\ a_1+a_2&=0. \end{align*}\]

Tämä on ristiriita, joten kun \(n=2\), niin \(N=2\).

Nyt on selvää, että \(N\):lle on olemassa raja ainakin joillain \(n\). Kun tämä oli tiedossa, päätin kokeilla, mitä arvoja saadaan lukujonon alussa mielivaltaisella \(n\):

\[\begin{align*} (a_1+a_0)(a_1+a_2)&=a_0-a_2\\ -\frac{1}{n}(a_1+a_2)&=a_0-a_2\\ -\frac{1}{n} a_1-a_0+\frac{n-1}{n} a_2&=0\\ -\frac{1}{n}(a_1+a_0)-\frac{n-1}{n}(a_0-a_2)&=0\\ -\frac{n-1}{n}(a_0-a_2)&=-1/n^2\\ a_0-a_2&=\frac{1}{n(n-1)}\\ -\frac{1}{n}(a_1+a_2)&=\frac{1}{n(n-1)}\\ a_1+a_2&=-\frac{1}{n-1}. \end{align*}\]

Kokeillaan vielä, mitä tapahtuu, kun \(k=2\):

\[\begin{align*} (a_2+a_1)(a_2+a_3)&=a_1-a_3\\ -\frac{1}{n-1}(a_2+a_3)&=a_1-a_3\\ -\frac{1}{n-1} a_2+\frac{n-2}{n-1} a_3-a_1&=0\\ -\frac{1}{n-1}(a_2+a_1)&= \frac{n-2}{n-1}(a_1-a_3)\\ a_1-a_3&=\frac{1}{(n-2)(n-1)},\\[14pt] -\frac{1}{n-1}(a_2+a_3)&=\frac{1}{(n-2)(n-1)}\\ a_2+a_3&=-\frac{1}{n-2}. \end{align*}\]

Näyttäisi siltä, että \(a_k+a_{k-1}=-\frac{1}{n-k+1}\) kaikilla \(k\), ja ristiriita tulee, kun \(a_k+a_{k-1}=-1\). Varmistetaan vielä, että ristiriita tosiaan seuraa tästä jokaisella \(n\):

\[\begin{align*} (a_k+a_{k-1})(a_k+a_{k+1})&=a_{k-1}-a_{k+1}\\ -a_k-a_{k+1}&=a_{k-1}-a_{k+1}\\ a_{k-1}+a_k&=0. \end{align*}\]

Nyt tarvitsee enää todistaa, että \(a_k+a_{k-1}=-\frac{1}{n-k+1}\) kaikilla \(k\). Tehdään tätä varten induktio-oletus, että tämä pätee \(k\):lla , ja osoitetaan, että tällöin se pätee myös \(k+1\):llä:

\[\begin{align*} (a_k+a_{k-1})(a_k+a_{k+1}) &=a_{k-1}-a_{k+1}\\ -\frac{1}{n-k+1} a_k-\frac{1}{n-k+1} a_{k+1}&=a_{k-1}-a_{k+1}\\ -\frac{1}{n-k+1}(a_{k-1}+a_k)&=\frac{n-k}{n-k+1}(a_{k-1}-a_{k+1})\\ a_{k-1}-a_{k+1}&=\frac{1}{(n-k)(n-k+1)}\\ (a_k+a_{k-1})(a_k+a_{k+1})&=a_{k-1}-a_{k+1}\\ -\frac{1}{n-k+1}(a_k+a_{k+1})&=\frac{1}{(n-k)(n-k+1)}\\ a_k+a_{k+1}&=-\frac{1}{n-k}=-\frac{1}{n-(k+1)+1}. \end{align*}\]

Induktiotodistus on nyt valmis, sillä alkuaskel on jo tehtävänannossa, jossa annettiin \(a_0+a_1=-\frac{1}{n}=-\frac{1}{n-1+1}\).

Siis \(a_k+a_{k-1}=-\frac{1}{n-k+1}\) kaikilla \(n\) ja \(k\), ja ristiriita tulee, jos ja vain jos \(a_k+a_{k-1}=-1\), eli kun \(n-k+1=1\) eli \(k=n\). Lukujonoa voidaan siis jatkaa \(a_n\):ään asti, mutta ei pidemmälle. Siispä \(N=n\).

Sain omasta ratkaisustani kuusi pistettä, koska unohdin mainita, että luvut \(a_0\) ja \(a_1\) on aina mahdollista löytää. Tämä on kuitenkin triviaalia, sillä \(a_1=-\frac{1}{n}-a_0\), joka on reaaliluku jokaisella reaaliluvulla \(a_0\).

Tehtävä 5: Olkoon \(f(n,2k)\) lukumäärä, joka kertoo kaikilla positiivisilla kokonaisluvuilla \(n\), \(k\), kuinka monella eri tavalla \(n \times 2k\) -lauta voidaan peittää täysin \(n\)k kappaleella kokoa \(2 \times1\) olevilla dominolaatoilla. (Esimerkiksi on \(f(2,2)=2\) ja \(f(3,2)=3\).) Etsi kaikki sellaiset positiiviset kokonaisluvut \(n\), että kaikilla positiivisilla kokonaisluvuilla \(k\) luku \(f(n,2k)\) on pariton.

Ratkaisu (Minea): Olkoon \(f(m,n)\) lukumäärä, joka kertoo erilaisten laatoitusten lukumäärän \(m \times n\) -laudalla. (Käytännöllisyyden vuoksi määritellään, että jos \(m=0\) tai \(n=0\), niin \(f(m,n)=1\).)

Väite 1: \(f(m,2n+1) = f(m,n) \pmod{2}\) kaikilla luvuilla \(n\) ja parillisilla luvuilla \(m\).

Todistus: Peilataan \(m \times (2n+1)\) laatoitukset keskisarakkeen suhteen. Nyt kukin peilattu laatoitus on samanlainen joko itsensä tai jonkun toisen alkuperäisen laatoituksen kanssa. Toiselle laatoitukselle peilautuvia laatoituksia on parillinen määrä, joten modulossa 2 tarkasteltuna \(f(m,2n+1)\) on kongruentti itselleen peilautuvien laatoitusten lukumäärälle.

Itselleen peilautuvissa laatoituksissa keskisarakkeen on pysyttävä muuttumattomana peilauksessa, joten keskisarakkeessa on oltava \(m/2\) pystysuoraa dominopalikkaa. Sen molemmille puolille jää \(m \times n\) kokoinen osa laudasta. Koska lauta on keskisarakkeen suhteen itselleen peilautuva, jokaista oikean puolen laatoitusta vastaa yksi mahdollinen vasemman puolen laatoitus. Itselleen peilautuvien laatoitusten lukumäärä on siis \(f(m,n)\), joten \(f(m,2n+1) = f(m,n) \pmod{2}\).

Väite 2: \(f(n,n) = 0 \pmod{2}\) kaikille parillisille \(n \geq 2\).

Todistus: Jos \(n \times n\) -laudan laatoitus peilataan lävistäjänsä suhteen, se ei voi peilautua itselleen. Jokaisella laatoituksella on peilattuna pari, joten \(n \times n\) -laatoitusten määrä on aina parillinen.

Ensimmäisestä väitteestä seuraa, että luku n toteuttaa vaatimuksen, jos ja vain jos luku \(\frac{1}{2}(n-1)\) toteuttaa.

Jos \(n \geq 2\), toisen väitteen perusteella luku \(n\) ei toteuta vaatimusta.

Jos \(n=0\), määritelmän mukaan luku \(n\) toteuttaa vaatimuksen, sillä \(f(m,0)=1\).

Etsityt luvut \(n\) ovat siis muotoa \(2^k-1\). (Huomaa, että tämä sisältää myös tapauksen \(n=0\).)