pdf  Solmu 2/2022

---

Solmun 3/2021 tehtävien ratkaisut

1. Ratkaise yhtälöpari

\[\begin{cases} x+y+\dfrac{x}{y}=19,\\ \dfrac{x(x+y)}{y}=60, \end{cases}\]

kun \(x,y\in\mathbb{R}\).

Ratkaisu. Merkitään \(a=x+y\) ja \(b=\frac{x}{y}\), \(y\neq 0\), jolloin saadaan yhtälöpari

\[\begin{cases} a+b=19,\\ ab=60. \end{cases}\]

Sijoittamalla ensimmäisestä yhtälöstä \(b=19-a\) yhtälöparin toiseen yhtälöön saadaan

\[a^2-19a+60=0,\]

jonka ratkaisut ovat \(a=4\) tai \(a=15\).

Tapaus \(a=4\): Tällöin \(x+y=4\) eli \(y=4-x\), joten

\[\frac{x}{4-x}=15.\]

Tästä seuraa \(60-15x=x\) eli \(16x=60\), joten \(x=\frac{60}{16}=\frac{15}{4}\) ja näin ollen \(y=4-\frac{15}{4}=\frac{1}{4}\).

Tapaus \(a=15\): Tällöin \(x+y=15\) eli \(y=15-x\), joten

\[\frac{x}{15-x}=4.\]

Tästä seuraa \(60-4x=x\) eli \(5x=60\), joten \(x=\frac{60}{5}=12\) ja näin ollen \(y=15-12=3\).

Yhtälöparilla on siis kaksi ratkaisua \((\frac{15}{4},\frac{1}{4})\) ja \((12,3)\).

2. Kolmen peräkkäisen kokonaisluvun neliöiden summa on yhtä suuri kuin seuraavien kahden kokonaisluvun neliöiden summa. Mitkä nämä peräkkäiset viisi kokonaislukua ovat?

Ratkaisu. On selvitettävä yhtälön

\[(x-2)^2+(x-1)^2+x^2=(x+1)^2+(x+2)^2\]

ratkaisut, kun \(x\in\mathbb{Z}\). Toiseen potenssiin korotukset tekemällä saadaan

\[3x^2-6x+5=2x^2+6x+5,\]

siis \(x^2-12x=x(x-12)=0\), joten \(x=0\) tai \(x=12\). Näin ollen kysytyt viisi peräkkäistä kokonaislukua ovat \(-2,-1,0,1,2\) tai \(10,11,12,13,14\).

3. Paperille on piirretty alla olevan kuvan mukainen neliöistä koostuva monikulmio. Kaksi neliötä väritetään punaisiksi ja loput neliöt erivärisiksi: yksi neliö vihreäksi, yksi keltaiseksi, yksi siniseksi ja yksi oranssiksi. Monikulmio leikataan irti paperista ja neliöiden yhtymäkohdissa \(90^\circ\) taitoksia tekemällä muodostetaan kuutio. Kuinka monella eri tavalla neliöiden värittäminen on mahdollista tehdä niin, että muodostetussa kuutiossa mitkään vierekkäiset sivut eivät ole samanvärisiä?

Ratkaisu. Numeroidaan neliöt seuraavasti:

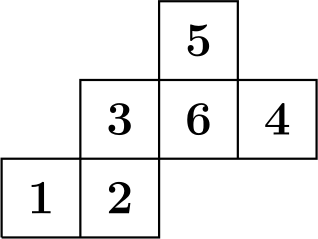
Taittelun jälkeen kaikki muut numerot paitsi 6 ovat numeron 1 naapureita, kaikki muut numerot paitsi 5 ovat numeron 2 naapureita ja kaikki muut numerot paitsi 4 ovat numeron 3 naapureita. Näin ollen vain sivut 1 ja 6, sivut 2 ja 5 tai sivut 3 ja 4 voidaan maalata punaisiksi. Kun mikä tahansa edellä mainituista kolmesta sivuparista maalataan punaisiksi, niin jäljelle jäävät sivut voidaan maalata vihreäksi, keltaiseksi, siniseksi ja oranssiksi \(4\cdot 3\cdot 2\cdot 1=24\) eri tavalla. Näin ollen erilaisia tapoja maalata kuvio vaaditulla tavalla on \(3\cdot 24=72\).

Huomaa, että koska värittäminen tehdään paperille piirrettyyn monikulmioon ennen leikkaamista ja taittelua, niin kuutiota kiertämällä saadut samanlaiset väritykset ovat erilaisia monikulmion värityksiä.

4. Kaksi henkilöä yritti arvioida ulkoilmakonsertin yleisömäärän. Toinen arvioi, että yleisöä oli 2700, ja toinen puolestaan arvioi, että yleisöä oli 3600. Osoittautui, että toisen arvion prosentuaalinen virhe oli kaksi kertaa niin suuri kuin toisen virhe. Lisäksi toinen aliarvioi ja toinen yliarvioi yleisön määrän. Kuinka paljon konsertissa oli yleisöä?

Ratkaisu. Merkitään pienempää virhettä \(p\) %. Tällöin on kaksi mahdollisuutta.

Tapaus 1: \(\displaystyle \frac{2700}{1-\frac{p}{100}}=\frac{3600}{1+\frac{2p}{100}}\). Yhtälön ratkaisu on \(p=10\), joten konsertissa oli yleisöä \(3000\).

Tapaus 2: \(\displaystyle \frac{2700}{1-\frac{2p}{100}}=\frac{3600}{1+\frac{p}{100}}\). Yhtälön ratkaisu on \(p=\frac{100}{11}\), joten konsertissa oli yleisöä \(3300\).

Näin ollen konsertissa oli yleisöä joko \(3000\) tai \(3300\).

5. Neliön sivun pituus on \(\sqrt{2}-1\). Molempia neliön lävistäjiä jatketaan toisesta päästä neliön sivun pituuden verran, ks. kuva alla.

(a) Kuinka pitkä on jana, joka yhdistää jatkeiden päätepisteet?

(b) Osoita, että neliössä on kärki, joka yhdessä jatkeiden päätepisteiden kanssa muodostaa tasakylkisen kolmion.

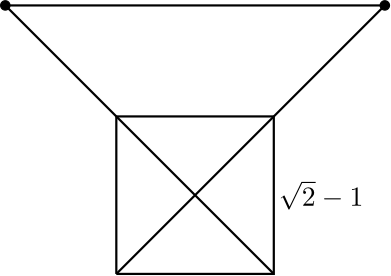
Ratkaisu. Käytetään alla olevaan kuvaan lisättyjä merkintöjä.

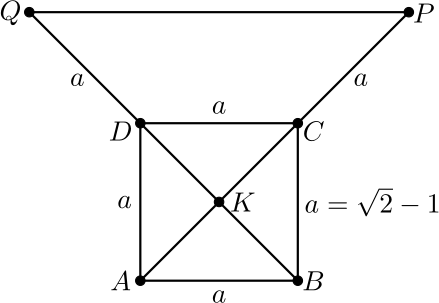
(a) Koska \(AC=\sqrt{2}a\), niin

\[KP=\frac{\sqrt{2}a}{2}+a=\left(\frac{\sqrt{2}}{2}+1\right)a.\]

Koska \(QKP\) on tasakylkinen suorakulmainen kolmio, niin

\[\begin{aligned} QP&=\sqrt{2}\left(\frac{\sqrt{2}}{2}+1\right)a=(\sqrt{2}+1)a\\ &=(\sqrt{2}+1)(\sqrt{2}-1)=2-1=1. \end{aligned}\]

(b) Koska

\[AP=\sqrt{2}a+a=(\sqrt{2}+1)a =(\sqrt{2}+1)(\sqrt{2}-1)=1,\]

niin \(AP=QP\). Näin ollen \(AQP\) on tasakylkinen kolmio. (Symmetrian vuoksi myös \(BPQ\) on tasakylkinen kolmio.)

6. Kuuden peräkkäisen kokonaisluvun summa kerrotaan kuuden seuraavan kokonaisluvun summalla. Osoita, että tällä tavalla saadun tulon jakojäännös luvulla 36 jaettaessa on aina sama.

Ratkaisu. Olkoon ensimmäinen kokonaisluku \(a\). Tällöin tulon ensimmäinen tekijä on

\[a+(a+1)+(a+2)+(a+3)+(a+4)+(a+5)=6a+15\]

ja toinen tekijä on

\[\begin{aligned} &(a+6)+(a+7)+(a+8)+(a+9)+(a+10)\\ &+(a+11) =6a+51. \end{aligned}\] Näiden tulo on \[\begin{aligned} (6a+15)(6a+51)&=36a^2+396a+765\\ &=36(a^2+11a+21)+9, \end{aligned}\]

jonka jakojäännös luvulla 36 jaettaessa on aina \(9\).

7. Määritä luvun \(11! +13!\) suurin alkutekijä. (Positiivisen kokonaisluvun \(n\) kertoma \(n!\) on kokonaislukujen \(1,\ldots,n\) tulo; esimerkiksi \(4!=1\cdot 2\cdot 3\cdot 4 = 24\).)

Ratkaisu. Koska

\[11! +13!=(1+13\cdot 12)11!=157\cdot 11!,\]

niin suurin alkutekijä on 157, joka on alkuluku.

8. Kaupan kassassa on 5, 10, 20, 50, 100 ja 200 euron seteleitä yhteensä 18 200 euroa. Ennen kuin viimeisin seteli lisättiin kassaan, niin jokaisen setelityypin lukumäärä oli kääntäen verrannollinen setelin arvoon. Kuinka monta 200 euron seteliä kassassa on?

Ratkaisu. Tehdään taulukko seteleiden lukumääristä ennen viimeisen setelin lisäämistä kassaan:

Näiden seteleiden arvo on

\[\begin{aligned} &5\cdot 40x+10\cdot 20x+20\cdot 10x+50\cdot 4x\\ &+100\cdot 2x+ 200\cdot x =1200x. \end{aligned}\]

Tiedämme, että

\[1200x+y=18200,\]

missä \(x\in\mathbb{N}\) ja \(y\in\{5,10,20,50,100,200\}\). Koska sekä \(1200\) että \(18200\) ovat jaollisia luvulla \(200\), niin on oltava \(y=200\). Näin ollen

\[1200x+200=18200\iff x=15,\]

joten \(200\) euron seteleitä on kassassa \(16\).

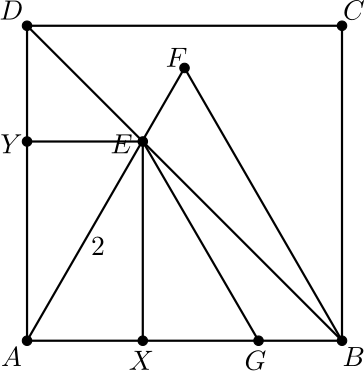
9. Tasasivuinen kolmio \(ABF\) on neliön \(ABCD\) sisällä alla olevan kuvan mukaisesti. Janan \(AE\) pituus on 2. Mikä on neliön \(ABCD\) pinta-ala?

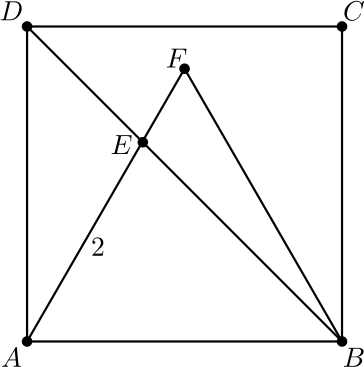
Ratkaisu. Piirretään kuvaan suorakulmio, jonka lävistäjä on \(AE\) ja sivut ovat neliön \(ABCD\) sivujen suuntaisia. Merkitään suorakulmion neliön sivuilla olevia kärkiä \(X\) ja \(Y\), katso alla oleva kuva. Koska \(EXB\) on tasakylkinen suorakulmainen kolmio, niin \(EX=XB\). Toisaalta, koska \(AEX\) on puolet tasasivuisesta kolmiosta \(AEG\) (katso kuva), niin \(AE=2\), \(AX=1\) ja \(XE=\sqrt{3}\). Näin ollen \(AB=AX+XB=1+\sqrt{3}\), joten neliön \(ABCD\) pinta-ala on

\[\big(1+\sqrt{3}\big)^2=4+2\sqrt{3}\approx 7{,}46.\]

10. Aino, Pekka ja Liisa pelaavat seuraavanlaista peliä. He valitsevat vuorotellen jonkin kokonaisluvun yhdestä kymmeneen ja lisäävät luvun aikaisemmin valittujen lukujen summaan. Aino aloittaa, Pekka on toinen ja Liisa on kolmas, jonka jälkeen vuoro siirtyy takaisin Ainolle jne. Selvyyden vuoksi jokainen pelaaja sanoo vuorollaan lukujen uuden summan. Pelin voittaa pelaaja, joka sanoo ensin luvun sata. Osoita, että tytöt voivat keskenään sopia pelistrategian, jolla pelin voittaa varmasti jompi kumpi heistä, eikä Pekka voi voittaa peliä.

Ratkaisu. Tytöt pelaavat seuraavalla strategialla: Aino lisää aina luvun \(1\) summaan, jonka Liisa on sanonut. Kun Pekka on lisännyt luvun \(i\) summaan, jonka Aino on sanonut, niin Liisa lisää luvun \(11-i\) summaan, jonka Pekka sanoo. Tällöin riippumatta siitä, minkä summan Pekka sanoo, kumpikin tyttö sanoo aina summan, joka on \(12\) suurempi kuin edellisellä kierroksella. Näin ollen, koska \(100=8\cdot 12+4\), niin jos Anna aloittaa luvulla \(4\), niin hän voittaa pelin, ja jos hän aloittaa luvulla \(5\), niin Liisa voittaa pelin.

11. Heitetään kuusi noppaa. Mikä on todennäköisyys, että saadaan vähintään neljä samaa silmälukua?

Ratkaisu. Täsmälleen \(4\) samaa lukua voidaan heittää

\[6\cdot \binom{6}{4}\cdot 1^4\cdot 5^2=2250\]

eri tavalla. Vastaavasti täsmälleen \(5\) samaa lukua voidaan heittää

\[6\cdot \binom{6}{5}\cdot 1^5\cdot 5^1=180\]

eri tavalla ja täsmälleen \(6\) samaa lukua voidaan heittää

\[6\cdot \binom{6}{6}\cdot 1^6\cdot 5^0=6\]

eri tavalla. Koska nämä eivät voi sattua yhtä aikaa ja kaikkien mahdollisten tapausten lukumäärä on \(6^6=46656\), niin kysytty todennäköisyys on

\[\frac{2250+180+6}{46656}=\frac{2436}{46656}=\frac{203}{3888}\approx 0{,}0522.\]

12. Positiiviselle reaaliluvulle \(x\) on voimassa \(x^2+\frac{1}{x^2}=7\). Määritä \(x^5+\frac{1}{x^5}\) laskematta luvun \(x\) arvoa.

Ratkaisu. Käytetään summan \(x+\frac{1}{x}\) potensseja. Koska

\[\left(x+\frac{1}{x}\right)^2=x^2+\frac{1}{x^2}+2=7+2=9\]

ja \(x\) on positiivinen, niin \(x+\frac{1}{x}=3\). Nyt

\[\begin{aligned} 3^3&=\left(x+\frac{1}{x}\right)^3=x^3+3x+\frac{3}{x}+\frac{1}{x^3}\\ &=x^3+\frac{1}{x^3}+3\cdot\left(x+\frac{1}{x}\right) =x^3+\frac{1}{x^3}+3\cdot 3, \end{aligned}\]

joten \(x^3+\frac{1}{x^3}=27-9=18\). Näin ollen

\[\begin{aligned} 3^5&=\left(x+\frac{1}{x}\right)^5=x^5+5x^3+10x+\frac{10}{x}+\frac{5}{x^3}+\frac{1}{x^5}\\ &=x^5+\frac{1}{x^5}+5\cdot\left(x^3+\frac{1}{x^3}\right)+10\cdot\left(x+\frac{1}{x}\right)\\ &=x^5+\frac{1}{x^5}+5\cdot 18+10\cdot 3. \end{aligned}\]

Tästä seuraa, että

\[x^5+\frac{1}{x^5}=243-90-30=123.\]

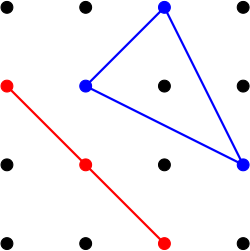
13. Alla olevassa kuvassa on 16 pistettä. Kuinka monella tavalla on mahdollista valita kolme pistettä niin, että muodostuu kolmio, jonka kärjet ovat valituissa pisteissä?

Ratkaisu. Kolmen pisteen valinta 16 pisteestä voidaan tehdä

\[\binom{16}{3}=\frac{16\cdot 15\cdot 14}{3\cdot 2\cdot 1}=560\]

eri tavalla. Näistä kolmion kärjiksi eivät kelpaa sellaiset valinnat, joissa kaikki kolme pistettä sijaitsevat samalla rivillä. Tällainen rivi voi olla vaakarivi, pystyrivi tai rivi, joka on \(90^\circ\) vinossa (diagonaalinen). Vaakarivillä kelpaamattomat pisteet voidaan valita neljällä eri tavalla, ja koska vaakarivejä on neljä, niin vaakariveiltä kelpaamattomat pisteet voidaan valita \(4\cdot 4=16\) eri tavalla. Vastaavasti pystyriveiltä kelpaamattomat pisteet voidaan valita myös \(16\) eri tavalla.

Vasemmalta oikealle alaspäin vinoilta riveiltä kelpaamattomat pisteet voidaan valita \(1+4+1=6\) eri tavalla, koska vasemmasta yläkulmasta oikeaan alakulmaan kulkevasta 4 pisteen rivistä valinta voidaan tehdä 4 eri tavalla ja tämän rivin ylä- ja alapuolella olevista vinoista 3 pisteen riveistä valinta voidaan tehdä yhdellä tavalla kummastakin. Vastaavasti vasemmalta oikealle ylöspäin vinoilta riveiltä kelpaamattomat pisteet voidaan valita myös \(6\) eri tavalla.

Näin ollen kelpaamattomia pistevalintoja on yhteensä

\[16+16+6+6=44,\]

joten kelpaavia pistevalintoja on \(560-44=516\). Alla olevaan kuvaan on piirretty yksi kelpaava kolmen pisteen valinta (näkyy värillisessä kuvassa sinisenä) ja yksi kelpaamaton valinta (näkyy värillisessä kuvassa punaisena).

14. Reaaliluvut \(x\) ja \(y\) toteuttavat ehdot \(x+3y=12\) ja \(x\ge 2y\ge 0\). Mitä arvoja \(x+2y\) voi saada?

Ratkaisu. Koska \(x\ge 2y\ge 0\), niin \(y\ge 0\) ja \(y\le \frac{1}{2}x\). Piirretään tilanteesta kuva \((x,y)\)-koordinaatistoon ja selvitetään pisteet \((x,y)\), jotka ehtojen perusteella kelpaavat mahdollisten arvojen \(C=x+2y\) laskemiseen.

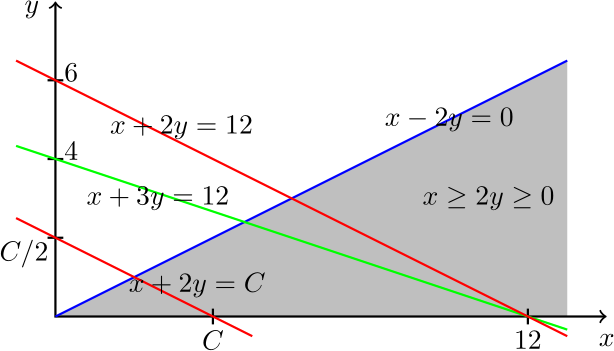
Pisteet \((x,y)\), jotka ovat suoralla \(x+3y=12\) ja ovat kuvassa harmaalla merkityllä alueella, kelpaavat. Vakion \(C\) mahdolliset arvot voidaan määrittää piirtämällä suoria, joiden kulmakerroin on \(-\frac{1}{2}\) ja jotka leikkaavat suoran \(x+3y=12\) harmaalla alueella. Tämän perusteella \(C\):n arvojen ala- ja yläraja saadaan kahden yhtälöparin ratkaisuista:

\[\begin{cases} x+3y=12,\\ x=2y, \end{cases}\ \text{ja}\quad \begin{cases} x+3y=12,\\ y=0. \end{cases}\]

Ensimmäisen yhtälöparin ratkaisu on \((\frac{24}{5},\frac{12}{5})\) ja toisen \((12,0)\). Näin ollen \(C\):n arvojen alaraja on \(\frac{24}{5}+2\cdot\frac{12}{5}=\frac{48}{5}=9{,}6\) ja yläraja on \(12+2\cdot 0=12\), joten \(9{,}6\le x+2y\le 12\).

15. Millä parametrin \(a\) arvoilla toisen asteen yhtälöllä

\[ax^2+a^2x+a=\frac{1}{a}\]

on kaksoisjuuri?

Ratkaisu. Kirjoitetaan yhtälö muodossa

\[ax^2+a^2x+a-\frac{1}{a}=0.\]

Yhtälöllä on kaksoisjuuri, jos sen diskriminantti on \(0\):

\[0=a^4-4a\left(a-\frac{1}{a}\right)=a^4-4a^2+4=(a^2-2)^2.\]

Näin ollen on oltava \(a^2=2\) eli \(a=\pm\sqrt{2}\).

16. Yksin tehdessään Pekalta kuluu työtehtävässä viisi tuntia ja Paavolta kuluu samassa työtehtävässä kuusi tuntia. Kun he tekevät työtehtävän yhdessä, niin heidän tuottavuutensa heikkenee jatkuvan kinastelun takia. Molempien työteho vähenee suhteessa yhtä paljon samalla prosenttimäärällä. Kuinka monta prosenttia heidän työtehonsa vähenee, kun yhdessä heillä kuluu työtehtävässä 3,5 tuntia?

Ratkaisu. Yksin tehdessään Pekka tekee viidesosan työtehtävästä tunnissa ja Paavo tekee vastaavasti kuudesosan. Jos he eivät vaikuttaisi toistensa työntekoon, niin he tekisivät yhdessä \(\frac{1}{5}+\frac{1}{6}=\frac{11}{30}\) työtehtävästä tunnissa, joka merkitsisi samaa kuin \(\frac{77}{60}\) työtehtävästä \(3{,}5\) tunnissa. Mutta koska he tekevät \(\frac{60}{60}\) työtehtävästä \(3{,}5\) tunnissa, niin heidän työtehonsa on \(\frac{60}{77}\) alkuperäisestä tehosta. Näin ollen heidän työtehonsa yhdessä työskennellessään vähenee

\[100\ \%-\frac{60}{77}\cdot 100\ \%=22{,}1\ \%.\]

17. Tiinalla on uusi työpaikka ja hän kulkee töihin omalla autolla. Ensimmäisenä työpäivänä hän ajoi 70 km/h keskinopeudella ja saapui töihin minuutin myöhässä. Toisena työpäivänä hän lähti liikkeelle samaan aikaan, ajoi 75 km/h keskinopeudella ja saapui töihin minuutin etuajassa. Kuinka pitkä työmatka Tiinalla on?

Ratkaisu. Ensimmäisenä päivänä Tiinan työmatka kesti \(x\) tuntia. Toisena päivänä aikaa kului \(\frac{2}{60}\) tuntia vähemmän kuin ensimmäisenä päivänä. Koska kuljettu matka oli molempina päivinä sama, niin

\[70x=75\left(x-\frac{2}{60}\right)\iff x=\frac{1}{2}=0{,}5.\]

Näin ollen Tiinan työmatka on

\[70\ \text{km/h} \cdot 0{,}5\ \text{h} =35\ \text{km}.\]

18. Jouluun on aikaa viisi päivää ja joulukuusessa on jäljellä viisi karkkia: kaksi niistä on marmeladia ja kolme on suklaata. Karkkeja ei voi tunnistaa käärepaperin perusteella. Hanna päättää syödä yhden karkin päivässä jouluun asti. Kumpi seuraavista on todennäköisempää: Hanna syö toisen (ja viimeisen) marmeladikarkin kolmantena päivänä vai hän syö kolmannen (ja viimeisen) suklaakarkin neljäntenä päivänä?

Ratkaisu. Jos Hanna syö toisen marmeladikarkin kolmantena päivänä, niin hänen pitää syödä ensimmäinen marmeladikarkki joko ensimmäisenä tai toisena päivänä. Vaihtoehtoja on siis kaksi. Jos Hanna syö kolmannen suklaakarkin neljäntenä päivänä, niin hänen on syötävä ensimmäiset kaksi suklaakarkkia kolmen ensimmäisen päivän aikana. Tämä merkitsee sitä, että kolmen ensimmäisen päivän aikana on yksi päivä, jolloin Hanna syö marmeladikarkin. Vaihtoehtoja on siis kolme. Näin ollen on todennäköisempää, että Hanna syö kolmannen suklaakarkin neljäntenä päivänä.

19. Heitetään kolikkoa neljä kertaa. Tämän jälkeen heitetään kolikkoa vielä niin monta kertaa kuin saatiin kruunia neljässä ensimmäisessä heitossa. Mikä on todennäköisyys, että saadaan vähintään viisi kruunaa?

Ratkaisu. On mahdollista saada vähintään viisi kruunaa vain, jos ensimmäisellä neljän heiton kierroksella saadaan kolme tai neljä kruunaa.

Tarkastellaan ensin tapausta, jossa neljällä ensimmäisellä kierroksella saadaan kolme kruunaa. Yhteenä vaihtoehtoja on \(2^4=16\), joista kolme kruunaa saadaan \(\binom{4}{3}=4\) eri tavalla. Tämän jälkeen heitetään kolikkoa kolme kertaa ja pitää saada vähintään kaksi kruunaa. Toisella kolmen heiton kierroksella vaihtoehtoja on yhteensä \(2^3=8\), joista vähintään kaksi kruunaa saadaan \(\binom{3}{2}+\binom{3}{3}=4\) eri tavalla.

Tarkastellaan sitten tapausta, jossa neljällä ensimmäisellä kierroksella saadaan neljä kruunaa. Neljä kruunaa saadaan vain yhdellä tavalla yhteensä \(2^4=16\) vaihtoehdosta. Tämän jälkeen heitetään kolikkoa neljä kertaa ja pitää saada vähintään yksi kruunaa. Tämä ei toteudu ainoastaan silloin, kun saadaan neljä klaavaa, joka on mahdollista vain yhdellä tavalla \(16\) vaihtoehdosta. Näin ollen toisella neljän heiton kierroksella vähintään yksi kruuna saadaan \(16-1=15\) eri tavalla.

Saadaan siis, että todennäköisyys saada vähintään viisi kruunaa on

\[\frac{4}{16}\cdot\frac{4}{8}+\frac{1}{16}\cdot\frac{15}{16}=\frac{47}{256}\approx 0{,}18.\]

20. Suorakulmio jaetaan kahdeksaksi neliöksi alla olevassa kuvassa esitetyllä tavalla. Keskikokoisen neliön pinta-ala on 100 cm\(^2\). Mikä on alkuperäisen suorakulmion pinta-ala?

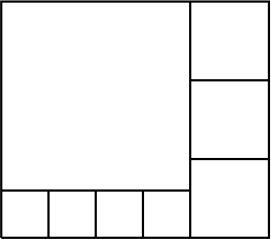
Ratkaisu. Keskikokoisten neliöiden sivun pituus on 10 cm. Suurin neliö voidaan jakaa 16 neliöön seuraavasti:

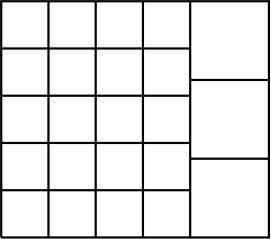
Tästä nähdään, että pienten neliöiden sivun pituus on

\[\frac{3\cdot 10\ \text{cm}}{5}=6\ \text{cm},\]

joten alkuperäisen suorakulmion pinta-ala on

\[20\cdot 6^2\ \text{cm}^2+ 3\cdot 100\ \text{cm}^2=1020\ \text{cm}^2.\]

Lähde: KöMaL
Käännös ja sovitus suomeksi: Mika Koskenoja