LASKUTOIMITUSTEN KERTAAMIEN

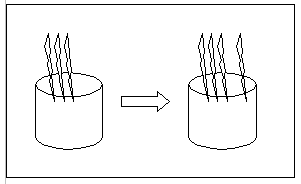
Tavoitteena on ymmärtää, mitä laskutoimituksia kulloinkin ratkaistavaan tehtävään tarvitaan sekä saada hyvä laskutoimitusten hallinta.

Palautetaan mieleen toisella luokalla opittuja asioita. Aloitetaan tarkastelemalla kuvia perusteellisesti. Tutkitaan kuvassa olevaa alkutilannetta, nuolen kuvaamaa muutosta sekä lopputilannetta.

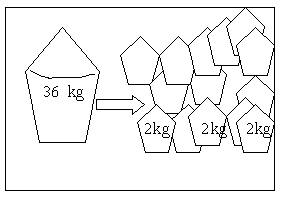
Tässä kuvassa lukee nuolen päällä, millainen muutos tapahtuu. Muutos kirjoitetaan nuolen alapuolelle laskutoimituksena.

TUTUSTUMINEN LUKUALUEESEEN 0-1000

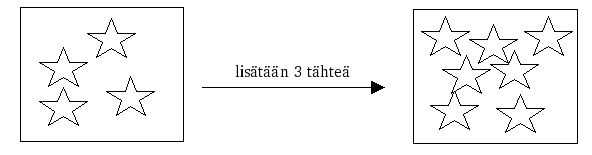
Lukualuetta lähestytään kahdella tavalla: a) lukumäärästä sekä b) mittaluvusta käsin. Tarkastellaan myös järjestyslukuja. Tavoitteena on, että luvut saavat sisältöä ja liittyvät konkreettisesti todellisuuteen. Varma lukukäsitys, lukujen varma tunteminen ja lukujen väliset suhteet vaativat lukujen ominaisuuksien perusteellista tutkimista. Luetellaan lukuja ja kerätään kokemuksia lukualueelta: käyttämällä lukuja, järjestyslukuja, mittalukuja. Tutkitaan aikaa ja massaa. Suoritetaan erilaisia mittauksia ja mittalukujen muunnoksia.

Aloitetaan lukujen luettelemisella. Huolimatta siitä, että lapsi osaa luetella lukuja suurillakin luvuilla, ei hän välttämättä hallitse lukukäsitettä. Lapsi omaa ehkä vain kuulokokemuksen ja laskemisrytmin. Esimerkiksi lukua 528 voidaan tarkastella monelta kannalta: mitä se on kirjoitettuna kirjaimin, millainen määrä riisiä se on, mitä saisi tuolla määrällä euroja; voidaan käyttää kaikkea mahdollista, mitä ympäristö tarjoaa.

Aloitetaan ykkösestä eteenpäin. Monotoninen luetteleminen saa lapset keksimään, miten luettelemista voitaisiin nopeuttaa: kaksittain, viisittäin, kymmenittäin. Ryhmiä, joilla lasketaan, on hyvä olla konkreettisesti esillä lapsen näkyvillä. Kotitehtäväksi annetaan erilaisia keräilytehtäviä: montako askelta kotiin, montako autoa kulkee kodin ohi tietyssä ajassa (suurkaupunkitehtävä!) Samalla opetellaan myös tukkimiehenkirjanpitoa. Näistä laaditaan yhdessä taulukkoja, joista tarkastellaan eri oppilaiden saamia tuloksia.

Luettelemista jatketaan ryhmittäin ja näin pohjustetaan lukujärjestelmää. Lapset muodostavat pieniä paketteja (5, 10 tai 50), joita yhdistellään edelleen suuremmiksi paketeiksi ja lasketaan lukumäärä.

Lasketaan kuinka paljon väkeä voisi olla stadionilla. Koska yksitellen laskeminen on mahdotonta, ryhmitellään pieneltä alueelta katsojat ja arvioidaan lukumäärä. Tässä tehtävässä ei ryhmittelemälläkään saa tarkkaa tulosta.

Lasketaan parkkitalon autot. Tiedetään, että parkkitalossa on 8 kerrosta ja ylimmäisen kerroksen autot ovat näkyvissä. Tarkkaa lukumäärää ei nytkään saada selville, koska ei tiedetä, onko jokaisessa kerroksessa sama määrä autoja.

Kaupasta saa monenlaisia pakkauksia, joiden avulla voi laskea ryhmittäin. Tulitikkuaskit, kirjekuoriniput, tulitikkupuntit, klemmarirasiat ovat hyviä ryhmittäin laskettaessa.

Jos lapsen eteen kaadetaan kasa riisinjyviä, hän tuskin pystyy kertomaan, kuinka monta riisinjyvää kasassa on. Pohditaan, millä menetelmällä riisinjyvät voisi laskea. Joku varmasti keksii jakaa riisinjyvät pieniin, mahdollisimman samankokoisiin kasoihin, joista lasketaan yhden kasan riisit. Tämän avulla arvioidaan riisien määrä. Tästä päästään helposti likiarvon käsitteeseen. Lapsi huomaa, ettei aina tarvitse tietää täsmällistä määrää (esim. montako riisiä on riisipuurossa).

Miksi tätä aihetta lähestytään suurien määrien ja hankalasti laskettavien esimerkkien kautta, esim. stadionin katsojat ja riisit? Tehtävien avulla halutaan osoittaa, ettei aina voida laskea - eikä aina ole tarpeenkaan laskea - tarkkaa määrää. Pyritään antamaan kokemus siitä, milloin riittää tietää määrä suunnilleen, milloin riittää vastaukseksi "paljon", milloin tarvitaan täsmällinen lukumäärä. Matematiikka tuo lapsille esiin todellisuuden ongelmia.

• Paljon: vesipisaroita järvessä,
• likimäärä: noin 5 dl vettä keittoon,
• täsmälleen: 5 ml yskänlääkettä.

Lapsen tulisi itse oppia, milloin tarvitaan mitenkin tarkkaa laskemista.

Likiarvo

Tämä on uusi käsite 3. luokalla. Likiarvon käsitettä lähestytään mittaamisen avulla. Lapsi valitsee itse mittayksikön, jota käyttää mittaamiseen. Tehtävästä riippuu, miten tarkasti tulos pitää saada selville. Pohditaan, miten tarkasti on syytä mitata lyijykynän pituus (cm tai mm), miten tuolin korkeus (cm), luokkahuoneen leveys (dm). Opetellaan mittaamaan viivoittimella. Käytetään mittavälineenä myös värisauvoja, sama asia mitataan myös mittanauhaa käyttäen. Työkirja on noin kahden oranssin sauvan korkuinen (dm-tarkkuus), jos halutaan mitata tarkemmin, otetaan lisäksi yksi punainen sauva (cm-tarkkuus).

Räätäli työskentelee senttimetrin tarkkuudella, arkkitehdin pohjapiirrokset ovat millimetrin tarkkuudella tehtyjä, mutta rakennusvaiheessa riittää senttimetrin tarkkuus.

Massan mittaaminen

Tässä vaiheessa ei tehdä eroa massan ja painon välillä. Lapsilla ei ole vielä fysikaalista tietoa, jossa ero tehtäisiin. Puhutaan massan mittaamisesta, mutta ei korjata, jos lapsi puhuu painosta, sanotaanhan arkipäivän puheessa: "Minun painoni on..." Se, mitä mitataan on todellisuudessa massa, jota mitataan esim. kilon punnuksilla.

Massan mittaamisen yhteydessä on ajatus tasapainosta todella tärkeä. Tämän opettamisessa havaintovälineenä on kaksikuppinen vaaka parempi kuin digitaalinen.

Massan mittaamisessa käytetään aluksi apuna värisauvoja.

1 valkoinen = 1 g

1 oranssi = 10 g

100 oranssia = 1 kg

Sadan oranssin sauvan mittaamisessa on lähes aina muutaman gramman heittoja. Lapsen on vaikea hyväksyä, että 997g on tässä 1kg.

Esimerkkejä tasapainotehtävistä

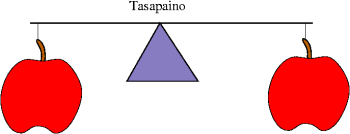
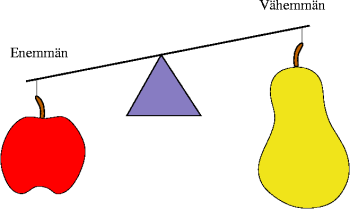
Taululla on kuvia elintarvikkeista. Tehtävänä on etsiä tyhjään vaakaan sellaisia, että vaa'at ovat kuvan suhteessa toisiinsa. Todellisella mittaamisella todennetaan, tuliko tehtävä oikein.

Lukuihin liitetään myös tuttuja tuotteita: 1/2 kg kahvia painaa vähemmän kuin 1 kg jauhoja. Mittaamista esiintyy tehtävissä tämän jakson jälkeen koko lukuvuoden ajan.

Abstraktit luvut

Luvut ovat saaneet tähän mennessä jo huomattavasti sisältöä. Numeromuodon ja sisällön välille on syntynyt yhteys. Kun tunnetaan paljon lukuja lukualueella 0-1000, tutustutaan lukujärjestelmiin. Luetellaan paljon lukuja, luetellaan yksittäin ja ryhmittäin. Otetaan lukuja esiin eri tavalla, esim. värisauvoilla siten, että yksikkö muuttuu (esim. valkoinen on 10, 50 tai 100)

Rakennellaan lukuja rahoilla. Näiden avulla saa parhaiten esille kymmenjärjestelmän. Jokaista yksikköä otetaan esille 9 kappaletta. Kun tulisi kymmenen vuoro, vaihdetaan seuraavaan yksikköön.

1. ja 2. luokilla on ryhmitelty paljon ja käytetty aikaa pienempiin lukujärjestelmiin. "Paketoimiset" 2. luokalla ovat tärkeitä kymmenjärjestelmän pohjustamiseksi.

Lasten tulee ymmärtää, että kymmenjärjestelmässä ryhmitellään lukuja kymmenittäin. On myös tärkeää, että lapset tiedostavat, että nollalla on paikkaa pitävä luonne.

Mitä tapahtuu, kun luku 12 siirretään yhden ruudun verran vasemmalle?

Mikä tulee ykkösten kohdalle? Voidaan käyttää lisäksi apuna värejä.

Jos luvun eteen lisätään nollia, määrä ei muutu.

Harjoitus värisauvoilla

Rakenna sauvoilla 460 siten, että valkoisen arvo on 10. = 4 oranssia + 6 valkoista/1 liila

Harjoitus kaarihelmitaululla

Luku 123

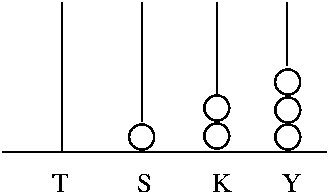
Kaarihelmitaululla on helppo työskennellä, koska 9 helmestä siirrytään seuraavan yksikön ykköseen. Muutos tulee helposti esille.

Esimerkkejä harjoituskirjasta 1. Lue helmitaulukuvista. Mitä lukuja ne merkitsevät?

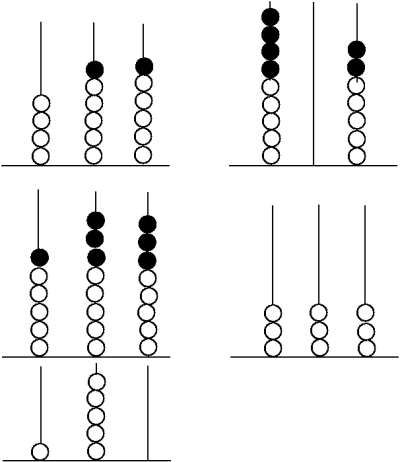
Mitä ajattelet seuraavista väittämistä? Perustele!

1. Se kuva, jossa on eniten helmiä, merkitsee suurinta lukua.
2. Ne, joissa on yhtä monta helmeä, merkitsevät yhtä suuria lukuja

2. Piirrä jokaiseen kuvaan yhteensä 10 helmeä. Yhteen tankoon et voi piirtää yhdeksää enempää. Tee aina useampia ratkaisuja. Kuvaa niillä seuraavia lukuja:

1. siinä on 9 kymmentä
2. siinä on kaksi kertaa niin paljon satoja kuin kymmeniä
3. siinä on samoja numeroita.

Erilaiset ehdot alleviivataan eri värein. Yhdellä kaarella voi olla korkeintaan 6 helmeä. (Mitä tarkoittaa korkeintaan 6? Voiko olla 6? 7? 5?) Muodosta 3-numeroisia lukuja siten, että satasten ja kymppien paikalla on sama luku. (Mikä on suurin mahdollinen luku? Kumpia tulee enemmän, parillisia vai parittomia lukuja?)

Varma lukukäsitys

On hallittava:

1. lukujen tunteminen
2. laskutoimitusten ymmärtäminen
3. erilaisten laskutapojen tunteminen

Lukutaulukkoja

Lukutaulukot ovat hyödyllisiä rakennettaessa lukukäsitettä. Ne vahvistavat lukujärjestelmiä ja niiden avulla on mahdollista laajentaa lukualuetta vähitellen.

Esimerkki

370	371	372	373	374	375	376	377	378	379
		382
		392
		402
		412

Täydennettäessä taulukkoa sanotaan luvut ääneen. Jotkut lapset etenevät numero kerrallaan, jotkut tajuavat taulukon "jujun" nopeasti. Autetaan oppilaan ajattelua pyytämällä häntä värittämään niiden lukujen paikat, joissa ykkösiä on 6 kappaletta sekä ympyröimään ne luvut, joissa on 8 kymppiä. Johtopäätös: Luvut suurenevat riveittäin edetessä yhdellä, sarakkeittain edetessä kymmenellä. Kehittyneempi vaihe edellisestä tehtävästä:

Ruudukon yläpuolella on apuna taulukko, jossa on
650, 651, 652, 653, ...
660, 661, 662, 663, ...
670 ....

Merkitse edelliseen taulukkoon ne luvut, joita kiekot merkitsevät (650, 655, 660, 665, 670, 675 ...) Opettaja antaa ensimmäisen luvun. Numerot ovat peitettyinä värikiekoilla kuten alla. (2.luokalla 0-100 -taulukoita, 3. luokalla 0-1000 -taulukoita) Voidaan jatkaa näin:

Kun oppilas täyttää edellisen kaltaista taulukkoa, hän huomaa tasaiset askeleet, muutoksen rytmin, miten muuttuvat ykköset, miten kymmenet.

Lukusuora

Käsitystä lukusuoran jaosta voidaan varmistaa esimerkiksi seuraavilla tavoilla:

• esitetään lukuja lukusuoralla aiempaa harvemmin (mittakaava muuttuu)
• yhtä numeroa lähestytään hitaasti
• suurennuslasia apuna käyttäen autetaan lasta ymmärtämään, mistä on kysymys tutkittaessa kahden merkityn luvun väliin jäävää aluetta
• voimme selittää, että aluksi näemme välimatkan sadasta toiseen, mutta jos lähestymme suurennuslasin avulla, näemme, että väli on jaettu kymmeniin
• samoin tutkitaan kahden kymmenen väliä

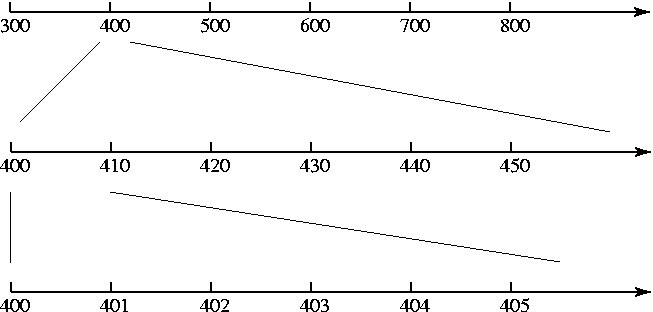
tutkitaan luvun

• ensimmäisestä numerosta, minkä kahden sataluvun välistä luku löytyy
• toisesta numerosta, minkä kahden kymmenen välistä luku löytyy
• kolmannesta numerosta, mikä on ykkösen paikka

Tätä tehdään yhdessä usein, sen jälkeen oppilaat paikantavat itse lukuja lukusuoralle.

Yhteisessä työskentelyssä voidaan tutkia myös jokin välin tarkentaen, esim. luku 325.

tutkitaan

• minkä kahden sadan välissä luku on
• ennen vai jälkeen lukua 350
• minkä kahden kymmenen välissä luku on
• luku on täsmälleen lukujen 320 ja 330 puolivälissä, merkitään kohta lukusuoralle esim. punaisella nuolella
• kumpaa satalukua lähempänä luku on? (välimatkan voi mitata 325 -> 300 ja 325 -> 400. Tässä tapahtuu pyöristämisen opettamista vaivihkaan)
• kumpaa kymmenlukua lähempänä? (koska se on puolessa välissä, niin yhtä kaukana molemmista)

Kypsytellään tehtävää muutama päivä ja palataan sitten tehtävään uudelleen uudella luvulla

701

• 700 ja 800 välillä, lähellä 700:aa
• minkä kahden kympin välissä (huomattava, että kymppien määrä on 0) Tässä helpottaa ykkösnaapureiden etsiminen, jos ykkösnaapuri on 700, ykkösten määrä on 0. EI kysytä kumpaa ykkösnaapuria lähempänä luku on, koska lapset tietävät, että ykkösnaapurit ovat aina yhtä kaukana toisistaan.

600

• tasaluvut ovat vaikeimpia lapsen ajattelulle
• lapsi ajattelee, että luku 600 on 600:n ja 700:n välissä tarkasteltaessa,
• minkä satalukujen välissä 600 on tarkastellaan naapurilukuja
• luku itse ei voi olla naapuri, joten luvut 500 ja 700 ovat satanaapurit. Tutkitaan luokan istumajärjestystä. Vierustoveri eli naapuri ei voi näyttää itseään, kun pitäisi osoittaa naapuriaan.

675

• muotoarvo, paikka-arvo, todellinen arvo
• mietitään leikkirahoja käyttäen, mitä tällä rahamäärällä voisi ostaa (eurojen kanssa vähän hankalaa, koska lapsilla on harvoin tällaisia summia käytössään)
• kuinka paljon jokin asia maksaa suunnilleen? Tällöin tulee esille pyöristäminen, pyöristämisen käsite.

188

• mihin kannattaa pyöristää?
• ei vielä kerrota pyöristämissääntöä, vaan lähdetään ratkaisemaan ongelmaa

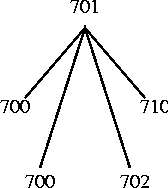
Mikä on se satanen, johon kannattaa pyöristää luku 450? Syntyy väittely, osa vastaa 400, osa 500. 500 valinneet puolustavat väitetään sillä, että sen voi maksaa käyttämällä 5 satasen seteliä. 401 on lähellä 400:aa, mutta ostosta ei saa neljällä satasen setelillä, kuuluu vastaväite! Lopulta tehdään sopimus, että pyöristetään suurempaan arvoon (ei ylöspäin, koska käsite ylöspäin tarkoittaa lapselle konkreettisesti ylöspäin)

Sama tehdään kymmenien pyöristämisen kanssa. Ongelmia ei ole lukutyyppien 453 ja 459 pyöristämisen kanssa. Analogia auttaa luvun 455 kanssa. Uusi ongelma on luvun 450 pyöristäminen kymmeniin. Joku huomaa kuitenkin pian, että pyöristämistä tarvita, koska on kysymys tasaluvusta.

Pyöristämisessä etsitään tasa kymmenlukua tai tasa satalukua, joka esittää mahdollisimman hyvin tätä lukua.

valkoinen on 100

• mikä värisauva kuvaa parhaiten lukua
• 301 on vaaleansininen
• 788 on tummanpunainen
• 290 on vaaleansininen
• 150 on vaaleanpunainen (ennen kuin on sovittu pyöristämissäännöstä, suurin osa ottaa tämän värisauvan esille)

valkoinen on 100

• 120 on vihreä
• 176 on iso ruskea ja vaaleanpunainen
• 69 on musta

Harjoitellaan lukusuoralla:

Pyydetään lapsia etsimään lukusuoralle sellaisia lukuja, joiden kymppeihin pyöristetty arvo on 150. Piirretään vihkoon ja merkitään luvut punaisilla pisteillä.

• Lapsi ei merkitse ensimmäisenä rajoja.
• Lapsi valitsee summamutikassa lukuja, esim. 149, 151.
• On lapsia, joilla on sisäinen tarve järjestykseen, ja he kokeilevat lukuja järjestyksessä
• On tärkeää, että lapset huomaavat, että myös luku 150 kuuluu tälle janalle. Väritetään alue lukusuoralle.

Väritä lukusuoralle alue, jonka luvut pyöristetään 400:aan. (350 - 449)

Tämän tehtävätyypin jälkeen siirrytään sanallisiin tehtäviin.

Esimerkkejä: 1. Leikkasin millimetripaperista noin 400 mm pitkän nauhan. Tiedän, että jos kirjoitan nauhan todellisen pituuden, niin kymppien kohdalle kirjoitan numeron 7. Miten pitkä paperinauhani mahtaa olla? (370- 379 mm)

• Mitä tarkoittaa noin 400 mm? miten se kirjoitetaan?
• Minkä pituiseksi lapset arvelevat 400 mm?
• Voidaan näyttää mittanauhalla. Mittanauha voi toimia myös lukusuorana niille, jotka yhä tarvitsevat apuvälineitä.
• Kuinka moninumeroista lukua etsimme?
• Tiedämme, että kymmenien paikalla on numero 7.
• Merkitään luvut, jotka pyöristetään 400:aan. (edelliselle lukusuoralle oli väritetty ne luvut, jotka pyöristetään 400:aan)
• Nyt lapsi havaitsee, että tehtävään on monta ratkaisua. Etsitään ne.

2. Pyöristän erään 3:een päättyvän luvun satasiin. Satasiin pyöristetty arvo on 600. Mikä luku tämä voi olla?

Apuvälineenä voi käyttää piirtoheittimellä sapluunaa, jossa numerot vaihtuvat.

Pahvista tehty sapluuna, jossa on aukot ykkösiä, kymmeniä ja satoja varten. Kalvosuikaleelle kirjoitetut numerot liikutetaan näkyviin.

Kerätään tiedot:

• monikonumeroisesta luvusta on kyse?
• mikä numero tunnetaan?
• mitkä ovat ne luvut, jotka pyöristetään 600:aan? (lukusuora tarvittaessa apuna)

3.Ajattelen erästä lukua. Sen sataseen pyöristetty arvo on 10 pienempi kuin kymmeniin pyöristetty arvo. Satojen paikalla on kolmonen. Mikä ajattelemani luku mahtaa olla?

• luku alkaa 300:lla
• kahdella eri tavalla pyöristetyn arvon ero on 10

Kehutaan, jos lapsi löytää yhden ratkaisun, rohkaistaan yhteisessä keskustelussa löytämään useampia ratkaisuja.

Lukujen muodostaminen

Kummasta kuvasta voidaan täydentämällä saada muodostetuksi enemmän lukuja?

• vasemmalla enemmän?
• oikealla enemmän?
• 10 numeroa, siis 10 ratkaisua?

Pyydetään oppilaita muodostamaan kaikki mahdolliset luvut. Käytetään apuna lukukortteja. Työskennellään yhdessä. Opettajalla on irtolapuissa sama muoto ja sama väri (ks. alla), kuin taululla. Kirjoitetaan niihin mahdolliset numerot. Kokeillaan ja löydetään monia ratkaisuja. Kokeileminen aloitetaan nollasta. Oppilaat huomaavat, ettei 0 käy satojen paikalle. Joissakin tapauksissa, esim. päivämäärissä ja kellonajoissa, on tapana kirjoittaa myös luvun alussa oleva nolla. Kerätään kaikki mahdolliset luvut ja kirjoitetaan muistiin. Huomataan, että nollalla on paikkaa pitävä merkitys kymmenien kohdalla.

Etsitään kolminumeroisia lukuja. Samanlaisiin kehyksiin voi laittaa vain saman numeron.

Etsitään lukupareja ja katsotaan kumpi luvuista on suurempi.

Esim.

251	261
350	360

Satojen paikalla on lukupareissa sama luku, eikä myöskään ykkösten arvolla ole eroa. Huomataan, että se luku on suurempi, jossa 6 on kymmenien paikalla, koska 6>5. Katsotaan useampia lukupareja, ennen kuin tehdään johtopäätös.

Lukujen muodostamiseen kuuluu aihepiiri, jossa käytetään kombinatoriikasta tuttuja asioita.

Esim. Luvuista 2, 3 ja 4 pitää kirjoittaa kaikki mahdolliset kolminumeroiset luvut. (Jos ei työskennellä lukukorteilla, on tehtävän annon oltava selvä sen suhteen, voiko samaa lukua käyttää useamman kerran) Lukukorteilla työskenneltäessä käytössä voi olla vain kolme korttia tai korttipino, jolloin yhtä numeroa on useita.

Kolmella kortilla muodostettavat luvut ovat:

234	324	423
243	342	432

Luvut voidaan etsiä järjestelmällisesti käyttäen apuna taulukkoa tai puudiagrammia.

Peli

Etsitään kolminumeroista lukua. Heitetään nopalla käytössä olevat numerot. Numeron (ks. alas) paikkaa ei saa vaihtaa. Kuka saa suurimman luvun?

Nopalla saadaan numerot 4, 6 ja 5. Niistä 4 sijoitetaan keskelle, 5 oikealle, 6 viimeiseen vapaaseen paikkaan eli vasemmalle.

Tämä peli johdattelee myös todennäköisyyteen. Nopassa on vain kaksi silmälukua, jotka ovat suurempia kuin 4. Mihin 4 kannattaa sijoittaa, jos se saadaan ensimmäisenä?

Esimerkki

Muodostettavan luvun on oltava pariton ja mahdollisimman pieni. Heitetyt luvut 5, 5 ja 6. Tässä tehtävässä voi olla tilanne, ettei tule parittomia, jolloin joudutaan toteamaan, että sattumanvaraisuus on aina olemassa eikä ratkaisua aina löydy.