Kolmannella luokalla matematiikan opetus alkaa kuuden viikon kertausjaksolla. Sen aikana palataan useasti 1. ja 2. luokilla opittuun oppiainekseen, jotta ennestään tutut käsitteet palautuvat mieleen ja uusi asia yhdistyisi niihin. Lapsen ajattelu on vielä konkreettista, joten abstraktion jatkumo on ajateltava perusteellisesti - on palattava alkuun ja yhä uudelleen varmistettava opittavaa käsitettä. Aistihavainnot ovat edelleen opetuksen perusta. Oppilas tekee itse havaintoja, kertoo niitä luokkatovereilleen ja oppii yhteisen väittelyn aikana. Opettaja ei korjaa virheitä, vaan lapsi huomaa itse, miten hänen on ajatuksiaan muutettava. Lämmin, salliva ilmapiiri mahdollistaa vapaan ajattelun.
Muutos edellisiin vuosiin verrattuna näkyy siinä, että oppilas ohjataan yhdistämään kokemuksiaan ja selvittämään yhteyksiä yhä tiedollisemmin. Hän kertoo toisille matemaattisia tilanteita. Opettaja ei tarjoa valmiina yhteenkuuluvaisuuksia matemaattisin termein, vaan oppilas kertoo kokemuksistaan omin sanoin. Opettajan tehtävänä on havainnoida, milloin konkreettiset kokemukset asiasta ovat riittävät. Matemaattista tekstiä tarkastellaan lähemmin (kirjassa sinisellä). Tällä varmistetaan, että oppilas myöhemmin pystyy ymmärtämään lukemaansa matemaattista tekstiä. Edelleen käytetään tarvittavaa toimintaa tekstin lukemisen ohella. Myös kuvan ja tekstin yhteyttä painotetaan. Näin saatujen kokemusten avulla lapsen omakohtainen matemaattinen ajattelu kehittyy.
Tutulla lukualueella 0-100 etsitään lukujen ja todellisuuden välisiä yhteyksiä. Niitä vahvistetaan mittaamalla, luettelemalla ja tietojen keräämisellä elävästä elämästä. Opetellaan erottamaan kappalemäärä, järjestysluku ja mittaluku kuvia tarkastelemalla. Kuvia esim. kaupasta ja korkeushyppypaikalta. Myös sanoista voi löytää vastaavat luvut:
| lukumäärä | järjestysluku | mittaluku | |
| sammal | 4 konsonanttia | 2. ja 4. kirjain ovat vokaaleja (a) | sanan pituus on 6 kirjainta |
| 2 vokaalia | 6. kirjain on L | mittanauhalla mitattuna 2 cm |
Muita esimerkkejä lukumäärästä, järjestysluvusta ja mittaluvusta:
Kotitehtäväksi keräilytehtävä: Tutki, mitä kaupassa myydään. Millaisina määrinä (pakkauksina)?
Oppilaiden pituuksia verrattaessa tehdään konkreettisia havaintoja. Vertaaminen antaa tietoa suhteista: toinen oppilas on jonkin verran pidempi kuin toinen. Hän on painavampi kuin toinen. Päästäkseen tarkkaan tulokseen oppilaan täytyy mitata mitattavan suhde mittayksikköön. Aluksi mitataan vaikkapa kynällä:kuinka monta kertaa kynä mahtuu kirjaan? Kirja on kahden kynän korkuinen.
Seuraavaksi otetaan 1 cm:n pituinen mittayksikkö: Kuinka monta kertaa 1 cm mahtuu vihkon sivuun? Vihko on 40 cm:n korkuinen. Lapsen matemaattisen ajattelun kehittymisen kannalta on tärkeää, että uudelle opeteltavalle asialle annetaan uusi käsitenimi, joka esitetään tuttuun tietoon pohjautuen. 2. luokalla kerättiin kokemuksia lukujen suuruudesta. Kolmannen luokan kertausjaksolla palautetaan niitä mieleen ja puetaan ne sanoiksi.
Tarkastellaan lukujen paikkoja erilaisilla lukusuorilla:
a) ______________________________________
0 10 20 30 (myös ykköset merkitty)
b) ______________________________________
0 10 20 30 (merkitty vain kymmenet)
c) ______________________________________
0 100
Lapsi esittää itse suullisesti, minkä avulla
suunnistaa: puolet sadasta on 50 ja puolet 50:stä on 25.
Opettaja auttaa, jotta ensimmäinen menee oikein.
On tärkeää varmistaa hyvä toisella luokalla opitun asian
osaaminen; nyt valmistellaan lukualuetta 0-1000.
Tarkastellaan lukua 27 ja huomataan, että se on lähempänä nollaa kuin esimerkiksi luku 84. Tutkitaan välimatkoja 27:stä 48:aan ja 84:ään. Todetaan, että välimatka 27:stä 84:ään on pidempi kuin 27:stä 48:aan. Huomataan, että lukujen suuruusjärjestys on kaikilla lukusuorilla sama.
Oppilaan matematiikkalaatikossa on noin 1 metrin pituinen langanpätkä. Kerrotaan muille oman langan pituus, kun sitä on verrattu opettajan langan pituuteen, joka on 1. Lapsi arvioi ensin, että opettajan lanka sisältyy hänen lankaansa 5 kertaa. Mittaamisen jälkeen saadaan tulokseksi 4; opettajan lanka sisältyi oppilaan lankaan 4 kertaa. Lapsilla on eri mittaisia lankoja. Opettaja sanoo, että hänen lankansa on nyt 3. Lapsi arvioi oman lankansa pituudeksi 15. Mittaamisen jälkeen opettajan langan todettiin sisältyvän oppilaan lankaan 12 kertaa. Näin oppilas saa kokemuksia lukujen välisistä suhteista. Lukualuetta 0-1000 voi myös käyttää tässä mittaamisleikissä. Leikitään myös pinta-aloilla: keltaista tarrapaperia verrataan kirjan sivuun: kuinka monta kertaa keltainen paperi mahtuu kirjan kanteen?
Kolmannella luokalla kiinnitetään erityistä huomiota lukujen muodostamiseen. Erotetaan selvästi toisistaan käsitteet numero ja luku. Esimerkiksi luku 12 on muodostunut numeroista 1 ja 2 (Opettaja palauttaa oppilaan mieleen kaikki 1. ja 2.-luokalla syntyneet mielikuvat luvusta 12). Erotellaan luvusta muodollinen arvo (=luvun muoto), paikallinen arvo (paikka-arvo) ja määrällinen arvo (todellinen arvo).
Numerot 3 ja 7 muodostavat luvun 37. Sen muodollinen arvo on 3 ja 7, koska se merkitään kolmosella ja seitsemällä. Sen paikallinen arvo on 3k = 3 kymmentä ja 7 ykköstä ja todellinen arvo on 30 ja 7. Luvun kokonaisarvo on 37. Apuvälineenä käytetään pussikkoa, jossa on taskut sadoille, kymmenille ja ykkösille. Kymmenten taskuun laitetaan 3 kappaletta kymmenlappuja ja ykkösten taskuun 7 kappaletta ykköslappuja. Mietitään, kuinka paljon lappuja pitäisi olla, jos luku olisi 73.
Lukuja muodostetaan myös seuraavan etsimistehtävän avulla: Etsi kaksinumeroisia lukuja, joissa on 3. Lapsi yrittää muodostaa jonkinlaisen etsimissysteemin: 13, 23, 33, 43, 53, 63, 73, 83, 93 ; 30, 31, 32, (33 on jo) 34, 35, 36, 37, 38, 39. Lasta pyydetään etsimään luvut myös lukusuoralta. Luvut piirretään taululla olevalle isolle lukusuoralle väriliiduilla.
Hauska tapa muodostaa kaksinumeroisia lukuja esim. numeroista 4,5 ja 9, jotka saavat toistua, on täydentää seuraava taulukko:
| 4 | 5 | 9 | |
| 4 | 44 | ||
| 5 | 59 | ||
| 9 |
Mikään luku ei jää pois; mikään ei tule kahta kertaa.
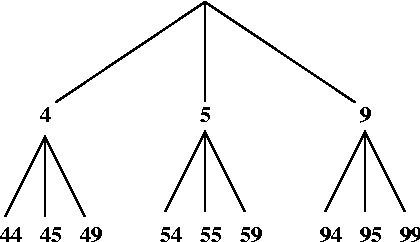
Lukuja muodostetaan myös puukaavion muodossa:

Tätä kuviota käytetään kombinatoriikan (yhdistelmäopin) yhteydessä. Oppilas tekee paljon tämäntyyppisiä tehtäviä. Kaikki tapahtuu kertausjaksolla kaksinumeroisilla luvuilla. Myöhemmin tehdään samoja tehtäviä lukualueella 0-1000.
Lukuja muodostetaan myös numerokorteilla: Muodosta se luku, joka on seitsemän kaksinkerta (7 kahdesti). Oppilas muodostaa korteista luvun 14. Hän asettaa pulpetille 7 + 7 pahviympyrää.Oppilasta pyydetään etsimään sellainen luku, joka on 10 suurempi kuin seitsemän yhdeksästi (=73). 'Etsi sellainen luku, joka on suurempi kuin 15, mutta pienempi kuin 19 ja jonka numeroiden summa on parillinen (=17). Oppilaalla on edessään numerokortit 1, 4, 7, 3, 1, 7 (korttien paikkoja ei saa vaihtaa keskenään). Oppilasta pyydetään etsimään 2-numeroinen luku siten, että tarpeettomat kortit nostetaan pulpetin yläreunaan. Oppilaan eteen jää seuraavassa pyydetyt luvut.
Etsi luku,
joka on pienin mahdollinen
joka on suurin mahdollinen
jonka ykkösten määrä on suurempi kuin kymmenten määrä
jonka ykkösten määrä on pienempi kuin kymmenten määrä.
Näistä vastauksista saadaan taululle luvut 11, 31, 41, 43, 71, 73 ja 77. Oppilas siis muodostaa kahdesta numerosta luvun.
Oppilasta pyydetään vastaamaan opettajan seuraaviin väittämiin 'oikein' tai' väärin'. Taululla on edelleen edellisestä tehtävästä muodostuneet luvut omilla korteillaan.
Tehtävä antaa tietoa opettajalle, erottaako lapsi käsitteet luku ja numero. Jos hän ei vielä erota, hän ei osaa sanoa, onko tehtävä oikein vai väärin.
Taululla on edellisen tehtävän luvut kortteina: 11, 31, 41, 43, 71, 73 ja 77. Taululla on myös neljä lappua, joissa on teksti: Numerot ovat samoja. Numerot ovat erilaisia. Numerot eivät ole erilaisia. Numerot eivät ole samoja. Oppilaalle annetaan tehtävä: 'Miten jaat nämä luvut kahteen ryhmään? Perustele!' Oppilas jakaa todennäköisesti luvut ryhmiin seuraavasti: 11, 77 ; Numerot ovat samoja. Numerot eivät ole erilaisia. 41, 31, 71, 73, 43; Numerot ovat erilaisia. Numerot eivät ole samoja.
Lukuja opeteltiin luokittelemaan jo 1. ja 2. luokalla. Luokittelutaitoja kehitetään edelleen. Lapselle annetaan kortit, joissa on seuraavat luvut: 11, 31, 43, 71, 73 ja 77. Tehtävänä on laittaa kupin sisälle kortit oiden luvut ovat suurempia kuin 41 ja kupin ulkopuolelle loput. Lapuilla on seuraavat kirjoitetut tekstit: pienempi kuin 41, ei suurempi kuin 41, ei pienempi kuin 41. Lapsen pitää valita näistä tekstivaihtoehdoista laput, jotka sopivat kupin ulkopuolelle.
Harjoitellaan luvun päättelemistä annetuista tiedoista: Lapselle annetaan paljon numerokortteja, joissa on 3, 4 ja 5. Tehtävänä on muodostaa niistä 2-numeroisia lukuja. Opettaja tarkkailee, onko lapsella jokin oma strategiansa lukujen muodostamisessa. ( 33, 34, 35, 43, 44, 45, 53, 54, 55) 'Etsi kaikki ne luvut, jotka ovat parillisia. Ota pois kaikki ne, jotka eivät ole tällaisia.' (jää 34, 44, 54) 'Voin kertoa luvustani: Numeroiden summa on 7. Ota se luku pois' (34),' Jos vaihdan kymmenten ja ykkösten paikalla olevia numeroita, saan parittoman luvun. Ota se pois' (54). 'Ota pois se luku, johon tämä ominaisuus ei sovi' (44). Mikä luku otettiin viimeisenä pois? (44)