PDF

Otsikkokuva

Modulaarisista laskutaulukoista

Visa Latvala ja Pekka Smolander
Matematiikan laitos, Joensuun yliopisto


Johdanto

Artikkelin tarkoituksena on tutustuttaa lukija modulaariseen yhteen- ja kertolaskuun. Nämä ovat ominaisuuksiltaan reaalilukujen yhteen- ja kertolaskun kaltaisia laskutoimituksia äärellisessä joukossa. Modulaaristen laskutoimitusten tarkasteluun on löydettävissä ainakin kaksi hyvää syytä: Ensinnäkin kyseiset laskutoimitukset ja yleisemmin äärelliset kunnat ovat keskeisessä roolissa modernissa tiedonsuojauksessa, ks. esimerkiksi [5, Luku 7]. Toiseksi modulaariset laskutaulukot ovat hyödyllisiä algebran yliopisto-opetuksen näkökulmasta, sillä ne antavat konkreettisia esimerkkejä, joiden avulla lähestyä algebrallisten struktuurien samanlaisuuden eli isomorfian käsitettä. Lukiolaiselle taulukot antavat esimerkin ei-standardista laskuopista, niitä voi tutkia ilman mitään tietoa abstraktista algebrasta.

Tässä esityksessä keskitytään modulaariseen kertolaskuun sen vuoksi, että yhteenlaskutaulukoita on niiden äärimmäisen säännöllisyyden vuoksi helppo muodostaa kynällä ja paperilla. Sen sijaan jo neljää alkiota suurempien kertolaskutaulukoiden muodostaminen kynällä ja paperilla alkaa olla työläs tehtävä. Tämä lienee keskeinen syy siihen, ettei ohessa esiteltäviä yleisiä kertolaskutaulukoita juuri löydy klassisista algebran oppikirjoista. Viimeisessä luvussa annetaan Maple-proseduuri, jota käyttäen laskutaulukoita voi muodostaa nappia painamalla.

Modulaaristen laskutoimitusten määritelmät

Olkoon $m\in\mathbf{N}$ luonnollinen luku. Kokonaisluvun $a\in\mathbf{Z}$ jakojäännös modulo $m$ on ehdoista

\begin{displaymath} a=km+r,\quad 0\le r<m, \end{displaymath}

yksikäsitteisesti määräytyvä ei-negatiivinen kokonaisluku $r$. Tässä luonnollisesti myös $k\in\mathbf{Z}$, ks. [5, Theorem 1.9].

Esimerkki. Luvun $15$ jakojäännös modulo 7 on $1$, sillä $15=2\cdot 7+1$. Luvun $25$ jakojäännös modulo $7$ on $4$, sillä $25=3\cdot 7+4$.

Modulaarinen yhteen- ja kertolasku määritellään kaikkien mahdollisten jakojäännösten modulo $m$ joukossa

\begin{displaymath} R(m):=\{\,0,1,\dots,m-1\,\} \end{displaymath}

asettamalla
$a\oplus b:=$ luvun $a+b$ jakojäännös modulo $m$,
$a\odot b:=$ luvun $ab$ jakojäännös modulo $m$.

Esimerkki. Laskemalla jakojäännökset modulo 4 todetaan, että yhteen- ja kertolaskutaulukot ovat muotoa

\begin{displaymath} \begin{array}{c\vert cccc} \oplus &0 &1 &2 &3\\ \hline 0 &0... ...\\ 1 &0 &1 &2 &3\\ 2 &0 &2 &0 &2\\ 3 &0 &3 &2 &1 \end{array}\end{displaymath}

Laskutaulukoita luetaan kuten koulusta tuttua kymmenen kertotaulua. Esimerkiksi

\begin{displaymath} 2\oplus 3=1 \end{displaymath}

eli tulos löytyy lukuun 2 liittyvän vaakarivin ja lukuun 3 liittyvän pystyrivin risteyskohdasta. Vastaavaan tapaan kertolaskutaulukosta havaitaan, että

\begin{displaymath} 2\odot 3=2. \end{displaymath}

Edelleen yhteen- ja kertolaskutaulukot modulo 5 ovat

\begin{displaymath} \begin{array}{c\vert ccccc} \oplus &0 &1 &2 &3 &4\\ \hline ... ...&2 &4 &1 &3\\ 3 &0 &3 &1 &4 &2\\ 4 &0 &4 &3 &2 &1 \end{array}\end{displaymath}

Kysymys. Millä tavalla luvun 0 esiintyminen eroaa toisistaan kertolaskutaulukoissa modulo 4 ja 5? Kyse on yleisestä ilmiöstä, joka liittyy siihen, että 5 on alkuluku, mutta 4 ei.

Edellisestä esimerkistä näkyy sääntö, jonka mukaan yhteenlaskutaulukot rakentuvat. Tässä esityksessä keskitytäänkin tarkastelemaan kertolaskutaulukoita, koska ne eivät rakennu yksinkertaisen säännön mukaisesti ja ovat siten vaikeammin esitettävissä. On kuitenkin korostettava, että yhteenlaskutaulukot ovat teoreettisesti erittäin tärkeitä. Esimerkiksi äärelliset Abelin ryhmät voidaan karakterisoida niiden avulla ([2, Theorem 10.7], tai [1, Theorem 1.22]). Toisaalta yhteen- ja kertolasku yhdessä muodostavat tärkeän esimerkin äärellisestä kunnasta tapauksessa, jossa $m$ on alkuluku. Mainittakoon myös, että kirjallisuudessa joukon $R(m)$ yhteenlaskutaulukolle käytetään tavanomaisesti merkintöjä $(\mathbf{Z}_m,+)$ ja $(\mathbf{Z}_m,\oplus)$.

Voidaan osoittaa, että $\oplus$ ja $\odot$ ovat aina vaihdannaisia ja liitännäisiä. Nämä ominaisuudet periytyvät kokonaislukujen vastaavista ominaisuuksista ([2, Theorem 2.7]). Vaihdannaisuus näkyy taulukoissa siten, että taulukot ovat symmetrisiä päälävistäjän suhteen.

Modulaarinen kertolaskuryhmä

Kertolasku $\odot$ ei yleisesti muodosta ryhmää joukossa

\begin{displaymath} R(m):=\{\,0,\dots,m-1\,\}, \end{displaymath}

sillä vaikkakin $1$ on neutraalialkio, niin esimerkiksi tapauksessa $m=4$ jakojäännöksellä 2 ei ole käänteisalkiota, ts.

\begin{displaymath} 2\odot x\ne 1 \end{displaymath}

kaikilla $x=0,1,2,3$. Sen sijaan alkuluvun $m$ tapauksessa $\odot$ muodostaa ryhmän joukossa $\{\,1,\dots,m-1\,\}$ (tämä perustellaan seuraavassa luvussa). Ryhmän määritelmä löytyy abstraktin algebran oppikirjoista, katso esimerkiksi [1].

Koska tarkoituksena on hyödyntää kertolaskutaulukoita äärellisten ryhmien isomorfiatarkasteluissa, rajoitetaan joukkoa $R(m)$ siten, että kertolaskun käänteisalkiovaatimus saadaan voimaan. Tämä suoritetaan siten, että joukosta $R(m)$ poimitaan taulukkoon mukaan vain ne jakojäännökset $a\in R(m)$, joille

\begin{displaymath} \textrm{syt}(a,m)=1. \end{displaymath}

Siis kertolaskua $\odot$ tarkastellaan joukossa

\begin{displaymath} R^*(m):=\{\,a\in\{\,1,\dots,m\,\}\mid \textrm{syt}(a,m)=1\,\}. \end{displaymath}

Esimerkiksi tapauksessa $m=24$ päädytään taulukkoon

\begin{displaymath} \left[ \begin{array}{cccccccc} 1& 5& 7& 11& 13& 17& 19& 23\\... ... 11& 1& 5\\ 23& 19& 17& 13& 11& 7& 5& 1 \end{array}\right]\ . \end{displaymath}

Taulukossa esitystä on yksinkertaistettu siten, että kerrottavien alkioiden vaaka- ja pystyrivit samoin kuin kertolaskumerkki $\odot$ on jätetty pois. Kerrottavat alkiot esiintyvät joka tapauksessa matriisin ensimmäisellä vaaka- ja pystyrivillä koska 1 on aina mukana taulukossa ja $1\odot a=a$ kaikilla $a\in R^*(m)$. Kertolaskun osalta käytetään jatkossa kaikkialla tätä yksinkertaistettya matriisiesitystä.

Edellisestä taulukosta huomataan, että joukon $R^*(8)$ jokainen luku toteuttaa yhtälön $x\odot x=1$. Tämä on erikoinen algebrallinen ominaisuus, joka ei yleisesti päde joukoille $R^*(m)$. Ominaisuuteen palataan viimeistä edellisessä luvussa.

Määritelmä.Eulerin funktio $\phi$ on sellainen kuvaus $\mathbf{N}\to\mathbf{N}$, että $\phi(m)$ ilmoittaa niiden lukujen $a\in\{\,0,1,\dots,m-1\,\}$ lukumäärän, joille $\operatorname{syt}(a,m)=1$.

Siis $\phi(m)$ ilmoittaa kuinka monta lukua joukossa $R^*(m)$ on. Voidaan osoittaa ([5, Theorem 6.5]), että funktiolle $\phi$ pätee kanoninen kaava

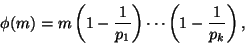
\begin{displaymath} \phi(m)=m\left(1-\frac1{p_1}\right)\cdots\left(1-\frac1{p_k}\right), \end{displaymath}

missä $\{\,p_1,\dots,p_k\,\}$ on luvun $m$ alkutekijöiden joukko, so. niiden alkulukujen joukko, joilla $m$ on jaollinen. Esimerkiksi

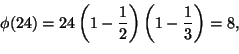
\begin{displaymath} \phi(24)=24\left(1-\frac12\right)\left(1-\frac13\right)=8, \end{displaymath}

sillä luvun $24=2^3\cdot 3$ alkutekijät ovat 2 ja 3.

Modulaarisen kertolaskuryhmän matemaattiset perustelut

Tässä luvussa tarkastellaan lyhyesti matemaattisia perusteluja sille, miksi $\odot$ muodostaa ryhmän joukossa $R^*(m)$. Tämä ei periaatteessa edellytä tietoja, jotka eivät tulisi vastaan lukion lukuteorian syventävällä kurssilla, katso esimerkiksi [3]. Jos luku tuntuu liian teoreettiselta, sen voi ohittaa ja palata asiaan tarvittaessa myöhemmin.

Kokonaisluku $p>1$ on alkuluku, jos luvulla $p$ ei ole muita positiivisia tekijöitä kuin 1 ja $p$. Lukuja $a,b\in\mathbf{Z}$ sanotaan keskenään jaottomiksi, jos lukujen $a$ ja $b$ suurin yhteinen tekijä $\textrm{syt}(a,b)$ on 1. Käytännössä luvut todistetaan usein keskenään jaottomiksi seuraavaa aputulosta käyttäen ([5, Theorem 2.2]):

Apulause 1. Kokonaisluvut $a$ ja $b$ ovat keskenään jaottomia, jos ja vain jos on olemassa $k_1,k_2\in\mathbf{Z}$ siten, että

\begin{displaymath} ak_1+bk_2=1. \end{displaymath}

Aiemmin on jo mainittu, että $\odot$ on liitännäinen ja vaihdannainen joukossa $R(m)$. On kuitenkin osoitettava, että kertolasku $\odot$ on laskutoimitus joukossa

\begin{displaymath} R^*(m)=\{\,a\in\{\,1,\dots,m-1\,\}\mid \textrm{syt}(a,m)=1\,\}, \end{displaymath}

eli on todettava, että tulo $a\odot b$ sisältyy joukkoon $R^*(m)$ kaikilla $a,b\in R^*(m)$. Tämä seuraa Apulauseesta 1: Jos $\textrm{syt}(a,m)=1$ ja $\textrm{syt}(b,m)=1$, niin $ak_1+mk_2=1$ ja $bl_1+ml_2=1$. Kertomalla yhtälöt puolittain saadaan
\begin{align*} 1&=(ak_1+mk_2)(bl_1+ml_2)\\ &=ab(k_1l_1)+m(ak_1l_2+bk_2l_1+mk_2l_2). \end{align*}
Siis $\textrm{syt}(ab,m)=1$ Apulauseen 1 nojalla. Edelleen jokaisella $a\in R^*(m)$ on joukossa $R^*(m)$ käänteisalkio kertolaskun suhteen, ts. yhtälöllä

\begin{displaymath} a\odot x=1 \end{displaymath}

on ratkaisu $x\in R^*(m)$ kaikilla $a\in R^*(m)$. Tämän perustelu on luontevinta suorittaa kongruenssin avulla: Kongruenssirelaatio modulo $m$ määritellään asettamalla

\begin{displaymath} a\equiv b\mod m \end{displaymath}

silloin kun erotus $a-b$ on jaollinen luvulla $m$ eli kun on olemassa $k\in\mathbf{Z}$ siten, että $a-b=km$. Kongruenssirelaatiota on aiemmin käsitelty Solmun artikkelissa [4].

Käänteisalkion olemassolokysymys palautuu yksinkertaisen lineaarisen kongruenssiyhtälön ratkaisemiseen ([5, Theorem 3.10]):

Apulause 2. Olkoon $m\in\mathbf{N}$ ja $a\in\mathbf{Z}$. Tällöin kongruenssiyhtälöllä

\begin{displaymath} ax\equiv 1\mod m \end{displaymath}

on ratkaisu $x\in\mathbf{Z}$ joka on yksikäsitteinen modulo $m$.

Olkoon $a\in R^*(m)$ ja olkoon $\tilde a$ kongruenssin

\begin{displaymath} ax\equiv 1\mod m \end{displaymath}

ratkaisun $x$ jakojäännös modulo $m$. Tällöin $\tilde a\in\{\,0,1,\dots,m-1\,\}$ ja

\begin{displaymath} a\tilde a\equiv 1\mod m. \end{displaymath}

Kongruenssin määritelmän mukaan erotus $a\tilde a-1$ on jaollinen luvulla $m$ eli on olemassa $k\in\mathbf{Z}$ siten, että $a\tilde a-1=km$. Tästä saadaan

\begin{displaymath} a\tilde a=km+1, \end{displaymath}

joten tulon $a\tilde a$ jakojäännös modulo $m$ on 1. Siis

\begin{displaymath} a\odot\tilde a=1. \end{displaymath}

Lopuksi $\tilde a\in R^*(m)$, sillä yhtälöstä $a\tilde a-km=1$ seuraa Apulauseen 1 nojalla, että $\textrm{syt}(\tilde a,m)=1$.

On osoitettu, että pari $(R^*(m),\odot)$ on ryhmä, sillä kertolasku $\odot$ on liitännäinen joukossa $R^*(m)$, luku $1\in R^*(m)$ on laskutoimituksen $\odot$ neutraalialkio joukossa $R^*(m)$ ja $\tilde a\in R^*(m)$ on alkion $a\in R^*(m)$ käänteisalkio laskutoimituksessa $\odot$.

Isomorfia-käsitteestä

Luvussa 2 todettiin, että $\phi(m)$ ilmoittaa ryhmän $(R^*(m),\odot)$ alkioiden lukumäärän. Syy siihen, miksi kertolaskutaulukot ovat käyttökelpoisia isomorfiatarkasteluissa piilee siinä, että Eulerin funktio ei ole injektio. Esimerkiksi

\begin{displaymath} \phi(5)=\phi(8)=\phi(10)=\phi(12)=4. \end{displaymath}

Näin ollen neljän alkion kertolaskuryhmät voidaan muodostaa joukoissa $R^*(5)$, $R^*(8)$, $R^*(10)$ ja $R^*(12)$. Näihin liittyvät taulukot ovat (vastaavassa järjestyksessä)

\begin{displaymath} \left[ \begin{array}{cccc} 1& 2& 3& 4\\ 2& 4& 1& 3\\ 3& 1&... ...\\ 3& 1& 7& 5\\ 5& 7& 1& 3\\ 7& 5& 3& 1 \end{array}\right], \end{displaymath}


\begin{displaymath} \left[ \begin{array}{cccc} 1& 3& 7& 9\\ 3& 9& 1& 7\\ 7& 1&... ... 5& 1& 11& 7\\ 7& 11& 1& 5\\ 11& 7& 5& 1 \end{array}\right]. \end{displaymath}

On luonnollista kysyä, kuinka monta rakenteeltaan erilaista ryhmätaulukkoa näiden neljän taulukon joukossa on? Tutkimalla taulukkoja
\begin{displaymath} \left[ \begin{array}{cccc} 1& 3& 5& 7\\ 3& 1& 7& 5\\ 5& 7&... ... 5& 1& 11& 7\\ 7& 11& 1& 5\\ 11& 7& 5& 1 \end{array}\right] \end{displaymath} (1)

havaitaan, että ne ovat rakenteeltaan identtiset; jos jälkimmäisessä käytetään symbolille 5 merkintää 3, symbolille 7 merkintää 5 ja symbolille 11 merkintää 7, saadaan ensimmäinen taulukko. Samalla tavalla havaitaan, että taulukot
\begin{displaymath} \left[ \begin{array}{cccc} 1& 2& 3& 4\\ 2& 4& 1& 3\\ 3& 1&... ...9\\ 3& 9& 1& 7\\ 7& 1& 9& 3\\ 9& 7& 3& 1 \end{array}\right] \end{displaymath} (2)

ovat rakenteeltaan identtiset. Seuraavaksi voidaan kysyä, ovatko esimerkiksi taulukot

\begin{displaymath} \left[ \begin{array}{cccc} 1& 2& 3& 4\\ 2& 4& 1& 3\\ 3& 1&... ...7\\ 3& 1& 7& 5\\ 5& 7& 1& 3\\ 7& 5& 3& 1 \end{array}\right] \end{displaymath}

identtiset? Vastaus on: eivät ole. Yksi (ikävä) tapa todeta tämä on kirjoittaa jälkimmäisen taulukon alkiot 3, 5 ja 7 kaikissa mahdollisissa järjestyksissä ja kussakin tapauksessa vertailla saatua taulukkorakennetta ensimmäiseen. Pidetään tässä tunnettuna, että luvut 1 taulukoissa vastaavat välttämättä toisiaan identtisissä taulukoissa. Menettely on työlästä ja useamman alkion tapauksessa käytännössä mahdotonta. Toinen (huomattavasti parempi) tapa, jota myöskään ei tässä yhteydessä perustella, on seuraava: havaitaan, että ensimmäisessä taulukossa yhtälöllä

\begin{displaymath} x^2=x\odot x=1 \end{displaymath}

on kaksi ratkaisua, kun taas jälkimmäisessä taulukossa yhtälöllä $x^2=1$ on neljä ratkaisua. Näin taulukot eivät voi olla rakenteeltaan identtiset (isomorfiset). Nimittäin isomorfisilla laskutoimituksilla kaikki algebralliset ominaisuudet ovat identtiset. Se, että alkio on itsensä käänteisalkio, on eräs algebrallinen ominaisuus, so. ominaisuus joka voidaan isomorfiakuvauksen avulla ''siirtää'' struktuurista toiseen.

Siis eräs silmiinpistävä peruste modulaaristen kertolaskutaulukoiden rakenteiden erilaisuudelle on se, että taulukoissa on eri määrä lukuja 1 päädiagonaalilla. Muita perusteita on löydettävissä muunlaisten algebrallisten ominaisuuksien avulla.

Huomautus. Voidaan osoittaa, että on olemassa vain kaksi neljän alkion ryhmärakennetta. Taulukot (1) ovat esimerkkejä Kleinin neliryhmästä. Taulukot (2) ovat puolestaan esimerkkejä neljän alkion syklisestä ryhmästä $(\mathbf{Z}_4,\oplus)$.

Tehtävä. Yhtälö $\phi(m)=8$ pätee arvoilla $m\in\{\,15,16,20,24,30\,\}$. Tulosta kertolaskutaulut joukoissa $R^*(15)$, $R^*(16)$, $R^*(20)$, $R^*(24)$, $R^*(30)$ Luvun 5 Maple-proseduurilla ja selvitä, kuinka monta rakenteeltaan erilaista näiden viiden taulukon joukossa on!

Maple-proseduuri modulaaristen kertolaskutaulukoiden tulostamiseksi

Maple-proseduuri, joka muodostaa listan ryhmän $R^*(m)$ alkioista: 

ryhma:=proc(m) 
local p,R,n,j: 
with(numtheory):
p:=phi(m): 
R:=array(1..p): 
j:=0: 
for n to m-1 do
  if gcd(n,m)=1 then
    j:=j+1: R[j]:=n:
  fi:
od:
evalm(R):
end:

Maple-proseduuri, joka muodostaa ryhmän $R^*(m)$ kertolaskutaulukon: 

kertotaulu:=proc(m) 
local p,T,R,i,j: 
with(numtheory):
p:=phi(m):
T:=array(1..p,1..p): 
R:=ryhma(m): 
for i to p do
  for j to p do
    T[i,j]:=R[i]*R[j] mod m:
  od:
od: 
evalm(T) 
end:

Viitteet

1
J. B. Fraleigh, A First Course In Abstract Algebra, Fourth edition, Addison-Wesley, 1989.

2
T. W. Hungerford, Abstract Algebra, Saunders College Publishing, 1990.

3
P. Jäppinen, A. Kupiainen ja M. Räsänen, Calculus 8, Lukuteoria ja logiikka, Otava, 1997.

4
T. Metsänkylä, Kongruenssi - lukuteorian kätevä apuväline, Solmu 3/1997-1998.

5
K. H. Rosen, Elementary Number Theory and Its Applications, Addison-Wesley, 1992.


Solmu 2/2003
16.5.2003