PDF

Otsikkokuva

Tehtävien ratkaisut


1. Ratkaisu. Toisen kierron jälkeen syntyvä neliö on peilikuva alkuperäisestä neliöstä pisteen $P$ suhteen. Jos $P$ ei ole alkuperäisen neliön sisällä, niin peilikuvalla ja alkuperäisellä neliöllä ei ole yhteistä pistettä. Tällöin kolmen neliön yhteisen pinta-alan täytyy olla suurempi kuin $2 \cdot 144\ \text{cm}^2 = 288\ \text{cm}^2$.

Oletetaan, että neliön sisällä on sellainen piste $P$, jonka ympäri neliötä $90^{\circ}$ kiertämällä saadaan kokonaispinta-alaksi $211\ \text{cm}^2$. Yhden neliön pinta-ala on $144\ \text{cm}^2$ ja päällekkäisten osien pinta-ala on $2 \cdot 144\ \text{cm}^2 - 211\ \text{cm}^2 = 77\ \text{cm}^2$. Vähentämällä yhteisen pinta-alan neliöstä saamme $144\ \text{cm}^2 - 77\ \text{cm}^2 = 67\ \text{cm}^2$.

Kuva 1.

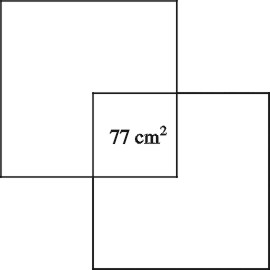
Ensimmäinen kierto siis lisäsi pinta-alaa $67\ \text{cm}^2$ (tummennettu alue kuvassa 1). Toista neliötä kierretään nyt $90^{\circ}$ pisteen $P$ ympäri. Ensimmäisen neliön kierretty kuva on toinen neliö ja toisen neliön kierretty kuva on kolmas neliö. Kokonaispinta-ala voi kasvaa kussakin kierrossa enintään saman verran kuin edellisellä kerralla, eli pinta-ala ei voi olla suurempi kuin $211\ \text{cm}^2 + 67\ \text{cm}^2 = 278\ \text{cm}^2$, joka on vähemmän kuin annettu $287\ \text{cm}^2$. Siten pistettä $P$ ei ole olemassa.


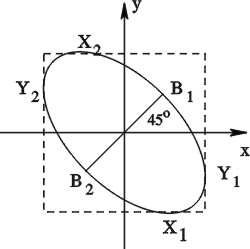
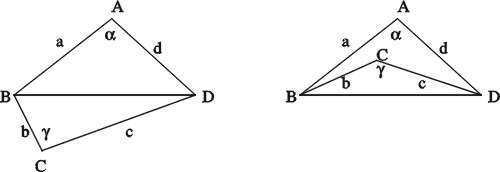
2. Ratkaisu. Ensimmäiseksi osoitamme, että minkä tahansa nelikulmion sivujen neliöiden summa on enintään neljä kertaa sen pinta-ala. Kuvan 2 merkintöjä käyttäen nelikulmion pinta-ala on
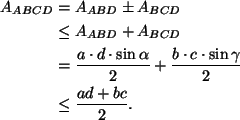
\begin{align*} A_{ABCD} &= A_{ABD} \pm A_{BCD}\\ &\le A_{ABD} + A_{BCD}\\ &=\f... ...+ \frac{b \cdot c \cdot \sin \gamma }{2}\\ &\le \frac{ad + bc}{2}. \end{align*}

Kuva 2.

Aritmeettisen ja geometrisen keskiarvon välisestä epäyhtälöstä saamme

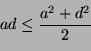
\begin{displaymath} ad \le \frac{a^2 + d^2}{2} \end{displaymath}

ja

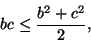
\begin{displaymath} bc \le \frac{b^2 + c^2}{2}, \end{displaymath}

ja siten

\begin{displaymath} 4A_{ABCD} \le a^2 + b^2 + c^2 + d^2, \end{displaymath}

kuten yllä on väitetty.

Jos vastaava epäyhtälö muodostetaan jokaiselle monitahokkaan sivulle ja epäyhtälöt summataan, niin vasen puoli on $4A$ ja oikea puoli $2Q$. Niinpä $4A \le 2Q$ ja siten $2A \le Q$.


3. Ratkaisu. Koska $\frac{1}{q} > \vert f(0)\vert$, niin $f(0)=0$. Kaikilla muilla $n$:n arvoilla $f$:n arvo on positiivinen kokonaisluku, sillä muuten ehdosta $f(n) = 0 < n$ seuraa, että

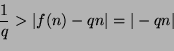
\begin{displaymath} \frac{1}{q} > \vert f(n)-qn\vert = \vert-qn\vert \end{displaymath}

ja siten

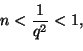
\begin{displaymath} n < \frac{1}{q^2} < 1, \end{displaymath}

mikä on mahdotonta. On helppo tarkistaa, että

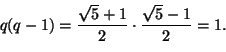
\begin{displaymath} q(q-1) = \frac{\sqrt{5}+1}{2} \cdot \frac{\sqrt{5}-1}{2} = 1. \end{displaymath}

Siten mille tahansa luonnolliselle luvulle $n$ on
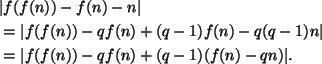
\begin{align*} &\vert f(f(n)) - f(n) -n\vert\\ &=\vert f(f(n))-qf(n) + (q-1)f(n) - q(q-1)n\vert\\ &=\vert f(f(n)) - qf(n) + (q-1)(f(n)-qn)\vert. \end{align*}
Koska kaikille reaaliluvuille pätee $\vert a+b\vert \le \vert a\vert + \vert b\vert$, voi edellinen itseisarvo olla korkeintaan
\begin{align*} &\vert f(f(n))-qf(n)\vert + \vert(q-1)(f(n) - qn)\vert\\ &=\vert f(f(n)) - qf(n)\vert + (q-1)\vert(f(n)-qn)\vert, \end{align*}
joka on vähemmän kuin

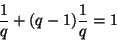
\begin{displaymath} \frac{1}{q} + (q-1)\frac{1}{q} = 1 \end{displaymath}

annetun ehdon mukaan. Siten

\begin{displaymath} \vert f(f(n)) - f(n) - n\vert < 1, \end{displaymath}

mikä on mahdollista vain, jos

\begin{displaymath} f(f(n)) - f(n) - n = 0, \end{displaymath}

koska $f(f(n))$, $f(n)$ ja $n$ ovat kokonaislukuja.


4. Ratkaisu. Oletetaan, että sieni on siis puoliympyrän muotoinen levy, jonka halkaisija on $AB$. Jos $A$ liikkuu pitkin $x$-akselia ja $B$ liikkuu pitkin $y$-akselia, niin puoliympyrän toisen puolen kehä liikkuu pisteen $O$ kautta. Siten mikään pyyhityn alueen piste ei ole 20 senttimetriä kauempana pisteestä $O$.

Kuva 3.

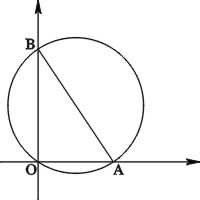
Ympyrän neljänneksen, jonka säde on $10$ cm ja keskipiste $O$, peittävät puoliympyrät, joiden halkaisijoina ovat $x$- ja $y$-akselit (Kuva 3).

Kuva 4.

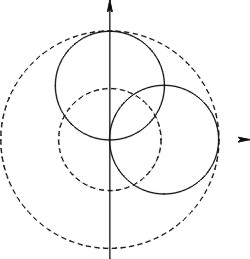
Jos $P$ on kahden kaaren väliin jäävä piste ja $OP$ leikkaa laajemman kaaren pisteessä $R$, niin pisteet $R_1$ ja $R_2$ ovat pisteen $R$ projektiot $x$- ja $y$-akseleilla. Tällöin $OR_1RR_2$ on nelikulmio, jonka lävistäjät ovat $RO = R_1R_2 = 20\ \text{cm}$. Jos piste $C$ on nelikulmion keskipiste, niin $OC = 10$ cm, ja $C$ sijaitsee pienemmällä ympyrän neljänneksen kaarella ja $P$ sijaitsee janalla $CR$. Piste $P$ sijaitsee siis kolmion $R_1RR_2$ rajaaman alueen sisällä. Kolmio $R_1RR_2$ on kokonaan puoliympyrän, jonka halkaisija on $R_1R_2$ ja kehäpiste $R$, sisällä. Siten pesusieni pyyhkii pisteen P.

Kuva 5.

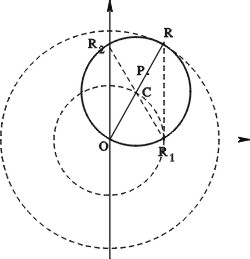
Edellä olevasta seuraa, että pesusienen pyyhkimä alue muodostaa neljännesympyrän, jonka halkaisija on $20$ cm ja säteen keskipistäänä $O$, joten pyyhitty alue on

\begin{displaymath} \frac{1}{4} \cdot 20^2 \pi = 100 \pi\ \text{cm}^2. \end{displaymath}


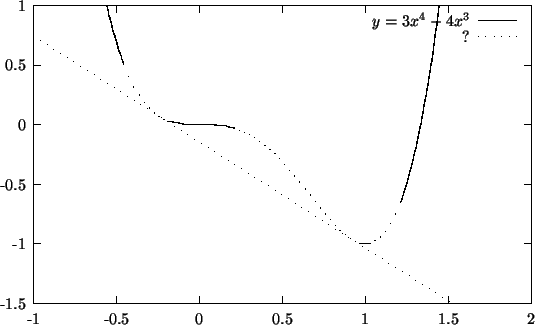
5. Ratkaisu 1. Kuvasta 6 nähdään funktion

\begin{displaymath} f(x) = 3x^4 - 4x^3 \end{displaymath}

kuvaaja. Pisteviiva esittää suoraa, jonka yhtälöä etsitään. Huomaa, että jos $x$:n tilalle sijoitetaan $x + \frac{1}{3}$ (Tätä sijoitusta, josta käytetään nimeä Tschirnhausin sijoitus, käytetään myös yleisen neljännen asteen yhtälön ratkaisemisessa. Se eliminoi kolmannen asteen termin.), mikä aiheuttaa kuvaajan siirtymisen $-\frac{1}{3}$ suhteessa akseliin, niin syntyvä neljännen asteen polynomi $f_1(x) = f(x+\frac{1}{3})$ ei sisällä kolmannen asteen termiä:
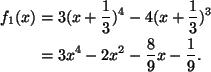
\begin{align*} f_1(x) &= 3(x + \frac{1}{3})^4 - 4(x + \frac{1}{3})^3 \\ &= 3x^4 - 2x^2 - \frac{8}{9}x - \frac{1}{9}. \end{align*}
Saamme $f_1$:n muotoon \begin{equation*} f_1(x) = 3(x^2 - \frac{1}{3})^2 - \frac{8}{9}x - \frac{4}{9}. \end{equation*}

Suora, joka koskettaa kuvaajaa

\begin{displaymath} y = 3(x^2-\frac{1}{3})^2 \end{displaymath}

kuvassa 7, on selvästi $x$-akseli, ja siten

\begin{displaymath} y = -\frac{8}{9}x - \frac{4}{9} \end{displaymath}

sivuaa käyrää $f_1(x)$ kahdessa pisteessä. Kysytty suora saadaan suorittamalla käänteinen sijoitus. Jos $x - \frac{1}{3}$ sijoitetaan $x$:n paikalle, suoran yhtälöksi saadaan \begin{equation*} y = -\frac{8}{9}(x - \frac{1}{3}) - \frac{4}{9} = -\frac{8}{9}x - \frac{4}{27}. \end{equation*}


\begin{picture}(1500,900)(0,0) \font\gnuplot=cmr10 at 10pt \gnuplot \sbox{\plotp... ....30,86.89){\usebox{\plotpoint}} \put(1232,82){\usebox{\plotpoint}} \end{picture}

Kuva 6.


\begin{picture}(1500,900)(0,0) \font\gnuplot=cmr10 at 10pt \gnuplot \sbox{\plotp... ...pt}{2.250pt}} \put(773.0,255.0){\rule[-0.200pt]{3.132pt}{0.400pt}} \end{picture}

Kuva 7.


5. Ratkaisu 2. Suora $y = ax + b$ sivuaa funktion $y = 3x^4 - 4x^3$ kuvaajaa korkeintaan kahdessa pisteessä jos ja vain jos polynomi

\begin{displaymath} p(x) = 3x^4 - 4x^3 - ax - b \end{displaymath}

sivuaa $x$-akselia kahdessa pisteessä eli sillä on kaksi juurta. Kuvaajan aste on neljä ja siten jokainen juuri on kaksoisjuuri, ja muita juuria ei ole. Jos juuret ovat $x_1$ ja $x_2$, niin $p(x)$ voidaan jakaa tekijöihinsä:
\begin{displaymath} p(x) = 3(x-x_1)^2(x-x_2)^2. \end{displaymath} (1)

Kertomalla oikea puoli auki saadaan
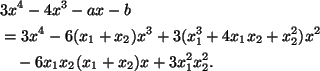
\begin{align*} &3x^4 - 4x^3 - ax - b\\ &= 3x^4 - 6(x_1+x_2)x^3 + 3(x_1^3 + 4x_1x_2 + x_2^2)x^2\\ &\quad - 6x_1x_2(x_1+x_2)x + 3x_1^2x_2^2. \end{align*}
Koska vastaavien kertoimien pitää olla yhtä suuria,
\begin{displaymath} x_1 + x_2 = \frac{2}{3}, \end{displaymath} (2)


\begin{displaymath} x_1^2 + 4x_1x_2 + x_2^2 = 0, \end{displaymath} (3)


\begin{displaymath} 6x_1x_2(x_1+x_2) = a, \end{displaymath} (4)


\begin{displaymath} -3x_1^2x_2^2 = b. \end{displaymath} (5)

Yhtälöstä (3) saadaan

\begin{displaymath} (x_1+x_2)^2 = -2x_1x_2 \end{displaymath}

ja edelleen yhdistämällä tämä yhtälön (2) kanssa saadaan $x_1x_2= -\frac{2}{9}$. Tämän jälkeen yhtälöstä (4) seuraa $a = -\frac{8}{9}$ ja edelleen yhtälöstä (5) $b = -\frac{4}{27}$.

Edellisestä seuraa, että suoran yhtälö voi olla vain

\begin{displaymath} y = -\frac{8}{9}x - \frac{4}{27}. \end{displaymath}

Tämä suora on kysytty ratkaisu, koska yhtälöiden (2) ja (3) juuret ovat reaalilukuja ( $x_1 = \frac{1}{3} - \frac{\sqrt{3}}{3}$ ja $x_2 = \frac{1}{3} + \frac{\sqrt{3}}{3}$) ja yllä olevat vaiheet voidaan suorittaa käänteisesti ja yhtälön (1) tekijät ovat reaalilukukertoimisia polynomeja.


5. Ratkaisu 3. Olkoon $a$ mielivaltainen reaaliluku. Yhtälö suoralle, joka sivuaa annettua käyrää pisteessä $(a, f(a))$, on

\begin{displaymath} y = f'(a)(x-a) + f(a). \end{displaymath}

Jos $b \neq a$, niin tämä on yhtenevä käyrän tangentille pisteessä $(b, f(b))$ jos ja vain jos
\begin{displaymath} f'(a) = f(b) \end{displaymath} (6)

ja
\begin{displaymath} f(a) - a \cdot f'(a) = f(b) - b \cdot f'(b). \end{displaymath} (7)

Yhtälöstä (6) saadaan jakamalla polynomilla $a - b \neq 0$, että
\begin{displaymath} a^2 + ab + b^2 - a - b = 0, \end{displaymath} (8)

ja yhtälöstä (7) samalla tavoin, että
\begin{displaymath} 9(a + b)(a^2 + b^2) - 8(a^2 + ab + b^2) = 0. \end{displaymath} (9)

Kohdasta (8) seuraa

\begin{displaymath} a^2 + ab + b^2 = a + b \end{displaymath}

ja sijoittamalla yhtälöön (9) saamme
\begin{displaymath} a^2 + b^2 = \frac{8}{9} \end{displaymath} (10)

Sijoittamalla tämä yhtälöön (8) saamme
\begin{displaymath} a + b - ab = \frac{8}{9} \end{displaymath} (11)

Koska yhtälöt (10) ja (11) johtavat neljännen asteen yhtälöön, esitellään uudet muuttujat $u = a + b$ ja $v = ab$. Saamme \begin{equation*} u^2 - 2v = \frac{8}{9}, \quad u - v = \frac{8}{9}. \end{equation*} Sijoittamalla $v = u - \frac{8}{9}$ saamme

\begin{displaymath} u^2 - 2u + \frac{8}{9} = 0. \end{displaymath}

Tämän juuret ovat $u_1 = \frac{2}{3}$ ja $u_2 = \frac{4}{3}$. Vastaavat arvot $v$:lle ovat $v_1 = - \frac{2}{9}$ ja $v_2 = \frac{4}{9}$.

Nyt $a$:n ja $b$:n arvot ovat yhtälöiden

\begin{displaymath} t^2 - u_1t + v_1 = 0 \end{displaymath}

ja

\begin{displaymath} t^2 - u_2t + v_2 = 0 \end{displaymath}

ratkaisuja. Ensimmäisessä tapauksessa $a = \frac{1}{3} - \frac{\sqrt{3}}{3}$ ja $b = \frac{1}{3} + \frac{\sqrt{3}}{3}$ ja toisessa tapauksessa juuret ovat yhtäsuuret, $a = b = \frac{2}{3}$. Koska määritelmän mukaan $a \neq b$, toinen tapaus ei ole ratkaisu.

Jos $a = \frac{1}{3} - \frac{\sqrt{3}}{3}$, niin $f'(a) = - \frac{8}{9}$ ja

\begin{displaymath} f(a) - a \cdot f'(a) = - \frac{4}{27}, \end{displaymath}

ja siten tangentin yhtälö pisteessä $(a, f(a))$ on \begin{equation*} y = -\frac{8}{9}x - \frac{4}{27}. \end{equation*} Koska kaikki vaiheet ovat käänteisiä, saadaan sama yhtälö tangentille pisteessä $(b, f(b))$.


Kuva 8.

Huomautuksia. Ratkaisun 3 ehdosta (8),

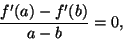
\begin{displaymath} \frac{f'(a)-f'(b)}{a-b} = 0, \end{displaymath}

saadaan ellipsi, jos $a$ ja $b$ esittävät koordinaattiakseleita (Kuva 8). Tämä ellipsi koostuu pisteistä $P(a,b)$, joille käyrän $y=4x^3-3x^2$ tangentit pisteissä $(a, f(a))$ ja $(b, f(b))$ ovat yhdensuuntaisia. Ellipsin akselit ovat yhdensuuntaisia koordinaattiakseleiden kulmien lävistäjille, ja ellipsin keskipiste on $C(\frac{1}{3},\frac{1}{3})$.

Lyhyemmän lävistäjän päätepisteet ovat $O$ ja $I(\frac{2}{3},\frac{2}{3})$.

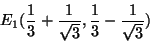
\begin{displaymath} E_1(\frac{1}{3}+\frac{1}{\sqrt{3}}, \frac{1}{3}-\frac{1}{\sqrt{3}}) \end{displaymath}

ja

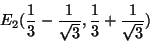
\begin{displaymath} E_2(\frac{1}{3}-\frac{1}{\sqrt{3}}, \frac{1}{3}+\frac{1}{\sqrt{3}}) \end{displaymath}

ovat kaksinkertaisen tangentin sivuamispisteitä. Tämä suhde tulee selväksi, jos ajattelee neljännen asteen yhtälön kuvaajan symmetrisyyttä pisteen $x=\frac{1}{3}$ suhteen. Tämä on symmetriakeskuksen abskissa kolmannen asteen derivaattafunktion kuvaajalle, joka esittää tangenttien kulmakerrointa. Jos kaksoistangentin yhtälö vähennetään neljännen asteen polynomista, saadaan neljännen asteen käyrä, joka on symmetrinen suoran $x=\frac{1}{3}$ suhteen. (Tämä on syynä sijoitukseen ratkaisussa 1.) Siten tangettipisteiden abskissat ovat symmetrisiä pisteen $x=\frac{1}{3}$ suhteen. Tämä piste sijaitsee kuvassa 8 suoralla $a+b=\frac{2}{3}$, joka on ellipsin pääakseli.

On helppo tarkistaa, että kaikilla neljännen asteen käyrillä, joilla on kaksinkertainen tangentti, on tämä ominaisuus, eli

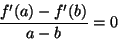
\begin{displaymath} \frac{f'(a)-f'(b)}{a-b} = 0 \end{displaymath}

esittää ellipsiä täsmälleen tässä tapauksessa. Kaikki tällä tavoin saadut ellipsit ovat samanlaisia, niiden eksentrisyys on $\frac{\sqrt{3}}{3}$ ja ne kaikki saadaan kuten kuvassa 8 on esitetty. Pikkuakseleiden päätepisteet esittävät vastaavan neljännen asteen käyrän käännepisteitä ja pääakseleiden päätepisteet esittävät kaksoistangenttien kosketuspisteitä.


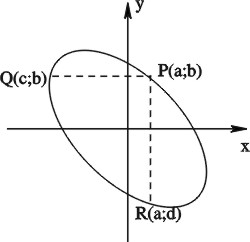
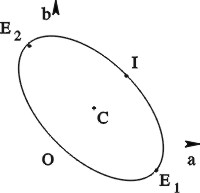
6. Ratkaisu 1. Jos muurahainen on käyrän pisteessä $P(a,b)$, niin yhtälöillä

\begin{displaymath} x^2 + bx + b^2 - 6 = 0 \end{displaymath}

ja

\begin{displaymath} y^2 + ay + a^2 - 6 = 0 \end{displaymath}

on reaalilukujuuret $a$ ja $b$. Siten diskriminantit $D_b = 24 - 3b^2$ ja $D_a = 24 - 3 a^2$ ovat ei-negatiivisia. Jos kumpi tahansa niistä on nolla, esimerkiksi $D_a = 0$ eli $\vert a\vert = 2\sqrt{2}$ (siten $b = -\frac{a}{2}$), niin muurahainen ei voi jatkaa kävelyään $y$-akselin suuntaisesti. Näin käy pisteissä $Y_1 (2\sqrt{2}, -\sqrt{2})$ ja $Y_2 (-2\sqrt{2}, \sqrt{2})$. Samoin, kun $D_b = 0$, eli muurahainen on pisteissä $X_1 (\sqrt{2}, -\sqrt{2})$ tai $X_2 (-\sqrt{2}, 2\sqrt{2})$, se ei voi jatkaa kävelyään $x$-akselin suuntaisesti.

Tämä on helposti nähtävissä, jos huomaa, että käyrä

\begin{displaymath} x^2 + y^2 + xy = 6 \end{displaymath}

on ellipsi (Kuva 9) ja pisteet $X_i, Y_i$ ovat pisteitä, joissa koordinaattiakseleiden suuntaiset tangentit sivuavat käyrää.

Kuva 9.

Jos muurahainen on pisteessä $P(a,b)$, joka ei ole mikään neljästä yllä mainitusta pisteestä, niin muurahainen voi kävellä kumpaan tahansa suuntaan. Jos $P$ ei ole lähtöpiste, niin muurahainen voi kävellä vain yhteen suuntaan, koska toinen suunta on tulosuunta.

Jos muurahainen kävelee esimerkiksi $x$-akselin suuntaisesti ja saapuu käyrän pisteeseen $Q(c,b)$, niin yllä olevan päättelyn mukaisesti $c \neq a$, ja luvut $a$ ja $c$ ovat kaksi yhtälön

\begin{displaymath} x^2 + bx + b^2 - 6 = 0 \end{displaymath}

reaalijuurta. Siten $a + c = -b$.

Kuva 10.

Vastaavasti, jos muurahainen kävelee $y$-akselin suuntaisesti ja saapuu pisteeseen $R(a, d)$ pisteestä $P$, niin $d + b = -a$ (Kuva 10).

Edellä olevasta seuraa, että kaikki muurahaisen kulkemat segmentit ovat sellaisia, että niiden päätepisteiden koordinaateista käyrällä kaksi neljästä ovat samoja. Näiden koordinaattien ja jäljelle jäävien summa on nolla: $a + b + c = 0$ ja $a + b + d = 0$.

Jos muurahainen esimerkiksi aloittaa kävelyn pisteestä $P_0(a,b)$ $x$-akselin suuntaisesti, sen polku kulkee seuraavien käyrän pisteiden kautta: $P_0(a, b) \to P_1(-a-b, b) \to P_2(-a-b, a) \to P_3(b,a) \to P_4(b, -a-b) \to P_5(a, -a-b) \to P_6(a;b)$.

Jos muurahainen ei saavu mihinkään pisteistä $X_i, Y_i$, niin sen kävely päättyy kuudennen segmentin loppuun. Jos muurahainen saapuu joihinkin pisteisiin $X_i, Y_i$, niin sen kävely loppuu jo aiemmin.


Huomautuksia. 1. Helposti havaitaan, että muurahainen voi saapua pisteeseen $X_i$, jos se kävelee $y$-akselin suuntaisesti: pisteeseen $X_1$ pisteestä $B_1(\sqrt{2},\sqrt{2})$ ja pisteeseen $X_2$ pisteestä $B_2(-\sqrt{2}, -\sqrt{2})$. Nämä ovat samoja pisteitä, joista muurahainen voi tavoittaa pisteet $Y_1$ ja $Y_2$.

Yhteenvetona voidaan todeta, että jos lähtöpiste on muu kuin $X_i$, $Y_i$, $B_i$, niin muurahaisen kävely päättyy kuuden osuuden jälkeen, jos lähtöpiste on $B_i$, niin kävely päättyy yhden osuuden jälkeen, ja jos lähtöpiste on $X_i$ tai $Y_i$, niin kävely päättyy kahden osuuden jälkeen.

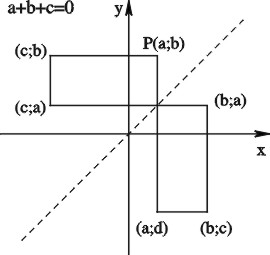
2. Käytettäessä merkintää $c=-a-b$ muurahaisen polku kulkee (erikoistapauksia lukuunottamatta) pisteiden $(a,b)$, $(c,b)$, $(c,a)$, $(b,a)$, $(b,c)$, $(a,c)$, $(a,b)$ kautta. Pisteiden koordinaatit ovat kaikki $a$, $b$ tai $c$ ja $a + b + c = 0$ (Kuva 11). Polku, kuten myös kuvaaja, on symmetrinen suoran $y=x$ suhteen.

Kuva 11.

Edellä olevilla lukukolmikoilla on mielenkiintoinen suhde tehtävän 5 mahdolliseen ratkaisuun. Jos alkuperäinen polynomi on kolmannen asteen polynomi

\begin{displaymath} f(x) = x^3-6x, \end{displaymath}

niin tämän tehtävän ellipsin yhtälö on

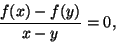
\begin{displaymath} \frac{f(x)-f(y)}{x-y}=0, \end{displaymath}

ja ellipsin pisteiden koordinaatit ovat lukupareja $(a,b)$, joille $f(a)=f(b)$.

Jokainen $f$:n arvo, paitsi paikallinen ääriarvo, saavutetaan kolmessa pisteessä ja muurahaisen kulkema polku vastaa tällaista kolmikkoa. Tällä esitystavalla ongelman ratkaisu on ilmeinen.


6. Ratkaisu 2. Kierretään käyrän kuvaajaa ja muurahaisen polkua $-45^{\circ}$. Tällöin käyrän yhtälö on (Kuva 12)

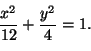
\begin{displaymath} \frac{x^2}{12} + \frac{y^2}{4} = 1. \end{displaymath}

Kuva 12.

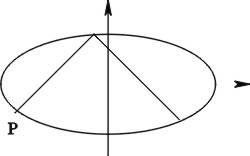
Kierretty muurahaisen kulkema polku koostuu osista, jotka ovat $45^{\circ}$ kulmassa koordinaattiakseleihin nähden. Ellipsin eksentrisyys on $\frac{b}{a} = \frac{1}{\sqrt{3}}$. Siten ortogonaalisen akseleiden yhtäläisyyden ja tekijällä $\sqrt{3}$ skaalaamisen jälkeen ellipsistä saadaan origokeskinen ympyrä, jossa muurahaisen polut muodostavat $+60^{\circ}$ ja $-60^{\circ}$ kulmat $x$-akseliin nähden (Kuva 13).

Kuva 13.

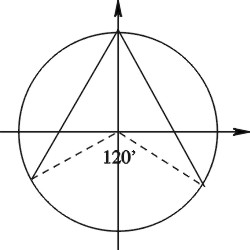
Muurahaisen paikka käyrällä kahden segmentin jälkeen lähtöpisteestä saadaan $120^{\circ}$ kulmana lähtöpisteeseen nähden. Kulman suunta riippuu muurahaisen kävelysuunnasta. Koska suunta säilyy samana koko muurahaisen matkan ajan, muurahainen välttämättä palaa lähtöpisteeseen kuuden segmentin jälkeen ja kävely päättyy.

Näin käy kaikissa muissa lähtöpisteissä, paitsi kuudessa erikoispisteessä. Neljä näistä pisteistä on sellaisia, joissa tangentit muodostavat $60^{\circ}$ kulman $x$-akselin kanssa. Jos muurahainen saapuu näihin pisteisiin, sen täytyy pysähtyä. Kaksi muuta pistettä ovat pystysuoran halkaisijan päätepisteet, joista muurahainen päätyy tangenttipisteisiin (Kuva 14).

Kuva 14.

Lähde: KöMaL, Volume 1, Number 1, December 2002, 46-55.
Käännös, ladonta ja kuvat: Jani Leinonen


Solmu 2/2003
16.5.2003