Otsikkokuva

Sattuman matematiikkaa II
- todennäköisyyslaskennan aksioomat

Terhi Kaarakka
Assistentti
Matematiikan laitos, Joensuun yliopisto

Solmu-lehden numerossa 2/2002 olleessa todennäköisyyslaskentaa käsittelevässä jutussa tarkasteltiin klassista ja geometrista todennäköisyyttä. Nyt mietitään sitä, miksi tarvitaan matemaattisesti täsmällisempi järjestelmä ja minkälainen sen pitäisi olla. Teksti pohjautuu pääosin teoksiin Todennäköisyyslaskenta osa 1 (Tuominen ja Norlamo)[2], Todennäköisyyslaskennan alkeita (Juve) [1] ja Todennäköisyyslaskenta (Tuominen)[3].

A. N. Kolmogorov

Frekvenssitulkinta

Koska klassinen todennäköisyys soveltuu vain pieneen ilmiöjoukkoon, niin käyttöön otettiin frekvenssitulkinta. Tarkastellaan satunnaisilmiöitä, joita on mahdollista toistaa rajattoman monta kertaa olosuhteiden pysyessä samanlaisina. Tällainen tulkinta soveltuu hyvin useisiin fysiikan ilmiöihin, joissa tarkastellaan suurta määrää olioita tai esimerkiksi uhkapeleihin, jotka ovat toistettavissa.

Määritellään suhteellinen frekvenssi olemaan tapahtuman esiintymiskertojen lukumäärän suhde toistojen lukumäärään, eli jos on tapahtuma ja tapahtuman esiintymiskertojen lukumäärä toistossa, niin suhteellinen frekvenssi on

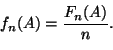
$\begin{displaymath} f_n(A)=\frac{F_n(A)}{n}. \end{displaymath}$

Todennäköisyyteen saadaan suhteellinen frekvenssi liitettyä seuraavasti

$\begin{displaymath} \mathbf{P}(A)={\rm ''}\lim_{n\to\infty}{\rm ''} f_n(A). \end{displaymath}$

Tämä on toistokokeissa aivan riittävä tapa ja näin saamme intuitiivisen todennäköisyyden. Kyseinen raja-arvo ei kuitenkaan täytä matemaattisen analyysin raja-arvon määritelmää, koska ei tiedetä onko se olemassa vai ei, joten se ei silloin matemaattisesti voi olla todennäköisyyden määritelmä.

Jossain tilanteessa pelkkä frekvenssitulkinta on intuitiivisestikin riittämätön. Mietitään tilannetta, jossa tietystä sairaudesta paranee todennäköisyydellä 0,99. Tämä tarkoittaa sitä, että kun tarkastellaan suurta (ideaalitilanteessa jopa rajatonta) määrää sairastuneita, niin parantumatta jää 1% sairastuneista. Käytännössä sairastuneelle ainoa merkittävä kerta on juuri oma sairastuminen, paraneeko hän vai ei. Tähän ei frekvenssitulkinta anna mitään vastausta.

Aksioomajärjestelmän tarpeellisuus ja vaatimukset

Klassisen todennäköisyyden vaatima symmetrisyys, geometrisen ja klassisen todennäköisyyden soveltuminen vain pieneen ilmiöjoukkoon ja frekvenssitulkinnan tarkan todennäköisyyden määrittelyn mahdottomuus johtivat keskusteluihin ja todennäköisyyslaskennan kehittymiseen.

Aksiomatisoinnissa halutaan pitää mielessä seuraavat tavoitteet

Matemaattinen teoria käsittelee käsitteiden välisiä suhteita. Perusolettamusten eli aksioomien ja joidenkin erityisolettamusten pohjalta päätellään deduktiivisesti näitä suhteita. Matematiikkaan ei suoranaisesti liity se, kuinka hyvin nämä teoriat sopivat empiirisiin ilmiöihin.
Mallin täytyy olla niin yleinen, että sen avulla voidaan kattaa mahdollisimman paljon erilaisia ilmiöitä. Eli näissä aksioomissa saa olla vain sellaisia piirteitä, jotka ovat ilmiöille yhteisiä, ei mitään yhteen tilanteeseen liittyviä erityispiirteitä.
Malli ei saa rakentua empiiristen tulosten varaan. Empiiriset tulokset auttavat mallin luomisessa ja suunnittelussa, mutta mallin täytyy olla abstrakti.

Toisin sanoen perustan täytyy sisältää vain mahdollisimman yksinkertaisia faktoja, joiden pohjalta lähdetään loogisesti päättelemään ja rakentamaan teoriaa. Perusolioille annetaan nimet, mutta muuten ne jätetään määrittelemättä, sillä muutoin jouduttaisiin ikuiseen kierteeseen: perusoliot pitäisi kuvailla ja kuvailuun tarvittaisiin olioita jne.

Matemaattisissa aksiomatisoinneissa peruskäsitteet otetaan usein käyttöön määrittelemättä. Geometriassa ei määritellä pistettä tai joukko-opissa joukkoa. Vastaavalla tavalla aksiomaattinen todennäköisyyslaskenta jättää määrittelemättä käsitteen todennäköisyys. Aksiomaattista todennäköisyyslaskentaa suunnitellessa oletetaan joukko-opin ja reaalilukujen ominaisuuksineen olevan käytettävissä, koska on lähes välttämätöntä käyttää niiden kieltä ja käsitteistöä hyväksi.

Aksioomat antavat tarkoituksella paljon vapauksia, koska niiden avulla halutaan mallintaa mahdollisimman monia ilmiöitä. Aksioomia voitaisiin ajatella esimerkiksi pelisääntöinä, joiden avulla matemaattisia pelejä pelataan, mutta pelejä on useita eikä haluta rajoittua ainoastaan yhteen peliin.

Teoriaa, aksioomien valinnan jälkeen, muodostetaan ja kasvatetaan loogisin päättelysäännöin. Esimerkiksi: Jos joukon kaikilla alkioilla on ominaisuus , niin millä tahansa joukon alkiolla on ominaisuus . Esim. ''nisäkäs on eläin, koira on nisäkäs, siis koira on eläin''. Eteenpäin mentäessä valitaan uusia oletuksia, suhteita ja selityksiä, ja näiden perusteella johdetaan taas uusia ominaisuuksia.

Aksiomatisoinnin taustalla on kauniin ja voimakkaan matemaattisen teorian luominen. Ihan puhtaalta pöydältä ei tietenkään aksiomatisointia kannata aloittaa, vaan on hyvä, että todennäköisyyksiä ja satunnaisilmiöitä on tutkittu jo aiemminkin sillä teorian luominen vaatii matemaattisen alueen tuntemusta, jolloin saadaan valittua mahdollisimman sopivat aksioomat.

Viime vuosisadan alussa mittateoria [säännöstö joukkojen mittaamiselle] oli kirjoitettu jo muotoon, jota pidetään matemaattisesti kauniina ja arvokkaana sekä sovelluskelpoisena. Tässä kirjoitelmassa joudutaan valitettavasti ohittamaan tämä teoria ja keskittymään vain siihen nojaavaan todennäköisyyslaskentaan. Mittateorian perusteella venäläinen Kolmogorov teki todennäköisyyslaskennan aksiomatisoinnin vuonna 1933. Kolmogorovia kutsutaankin usein, ja aivan oikeutetusti, todennäköisyyslaskennan isäksi.

Aksiomatisoinnin jälkeen rakennettiin todennäköisyyslaskennan teoriaa puhtaasti loogisen tiedon nojalla, ei kokemuksien tai intuition mukaan. Todennäköisyyslaskennan tarkoitus on kuitenkin mallintaa reaalimaailman ilmiöitä, niin kokonaan ei voida tai saadakaan unohtaa kokemuksia ja empiirisiä kokeita.

Todennäköisyyslaskennan aksioomat

Määrittelemme seuraavana todennäköisyysavaruuden eli matemaattisen mallin, johon pohjautuen voimme käsitellä erilaisia satunnaiskokeita. Satunnaiskokeet ovat kokeita, joiden tulos on varmasti tiedossa vasta kokeen tekemisen jälkeen.

Tarkastellessamme satunnaiskoetta täytyy ensimmäisenä päättää, mitkä ovat kokeen tulosmahdollisuudet eli alkeistapaukset. Kaikki alkeistapaukset yhdessä muodostavat perusjoukon $\Omega$ .

Otetaan esimerkkinä kahden nopan heitto. Alkeistapauksiksi on järkevää valita kaikki järjestetyt parit , missä sekä että saavat arvot yhdestä kuuteen eli . Yhteensä näitä alkeistapauksia on 36 ja ne muodostavat perusjoukon.

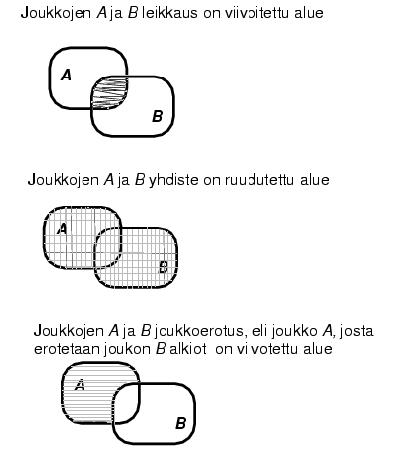
Toiseksi tarvitsemme kokoelman tapahtumia eli perusjoukon $\Omega$ osajoukkojen muodostaman kokoelman, jota merkitään kirjaimella $\F$ . Näitä joukkoja, jotka muodostavat kokoelman $\F$ , kutsutaan tapahtumiksi. Tapahtuman sattumisella tarkoitetaan, että kokeen tulos $\omega$ kuuluu tähän valittuun joukkoon eli $\omega \in A$ . Erilaisia tapahtumia voidaan kuvata joukkojen joukko-operaatioina. Oheisessa kuvassa on esitetty joukkojen ja leikkaus $A \cap B$ , yhdiste $A \cup B$ ja joukkoerotus $A \backslash B$ .

Satunnaiskokeiden peruskäsitteitä voidaan kuvata matemaattisesti joukko-operaatioiden avulla artikkelin lopussa olevan taulukon mukaan.

Kun tarkastelemme joukkoa, jonka kaikki alkiot pystymme luettelemaan, kannattaa tapahtumien joukkona käyttää kaikkia niitä joukkoja, joita alkeistapauksista voidaan muodostaa yhdistelemällä. Usein tämä ei ole mahdollista: jos vaikka tarkastelemme hehkulapun elinikää, niin emme pysty numeroimaan kaikkia mahdollisia aikoja, jonka lamppu voi kestää. Tämän ongelman välttämiseksi määritellään käsite $\sigma$ -algebra, jossa voimme käyttää tapahtumiin joukko-operaatioita. Tässä sivutaan nyt mittateoriaa, joka jätetään käsittelemättä, mutta yliopistossa pääsette tutustumaan siihenkin.

Perusajatuksena on, että tapahtumia halutaan olevan numeroituvat alkeistapauksien muodostamien joukkojen yhdisteet ja leikkaukset, näiden äärelliset yhdisteet ja leikkaukset sekä myös näiden kaikkien joukkojen erotukset. Seuraavana määritellään, milloin joukkojen kokoelma $\F$ on $\sigma$ -algebra. Hakasuluissa on selitystä matemaattisessa muodossa oleville ehdoille.

Määritelmä. Kokoelma $\F$ perusjoukon $\Omega$ osajoukkoja on $\sigma$ -algebra, jos

$(\sigma A_1)$: $\Omega \in \F$ . [Koko perusjoukko $\Omega$ on mahdollinen tapahtuma.]
$(\sigma A_2)$: Jos $A \in \F$ , niin $A^C \in \F$ . [ Jos on mahdollinen tapahtuma, niin myös joukon komplementti eli tilanne, että ei satu, on myös mahdollinen tapahtuma.]
$(\sigma A_3)$: Jos $A_i \in \F$ ( $i=1,2,\cdots$ ), niin $\bigcup_{i=1}^\infty A_i \in \F$ . [Jos ääretön määrä joukkoja ovat tapahtumia, niin myös $\bigcup_{i=1}^\infty A_i \in \F$ eli se, että jokin tapahtuu, on tapahtuma.]

Seuraavana tarkastelemme todennäköisyyttä: Tapahtuman eli kokoelman $\F$ alkion todennäköisyys $\mathbf{P}(A)$ on reaaliluku, jonka täytyy olla yksikäsitteisesti määrätty, kun tapahtuma $A \in \F$ on annettu. Toisin sanoen $\mathbf{P}$ on funktio $\F \to \R$ eli $\mathbf{P}$ on funktio kokoelmalta $\F$ reaalilukujen joukkoon. Tarvitsemme nyt kunnollisen määritelmän tälle kuvaukselle (=funktiolle) $\mathbf{P}$ .

Määritelmä. Kuvaus $\mathbf{P}: \F \to \R$ on todennäköisyys, jos

(TN)

$\mathbf{P}(A)\geq 0$ kaikilla $A \in \F$ . [Kaikkien tapahtumien todennäköisyydet ovat positiivisia tai nollia.]

(TN)

$\mathbf{P}(\Omega)=1$ . [Varman tapahtuman todennäköisyys on yksi.]

(TN)

(täysadditiivisuus) Jos $A_i \in \F (i=1,2,\cdots)$ ja $A_i \bigcap A_j=\emptyset$ kaikilla $i \neq j$ , niin

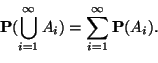
$\begin{displaymath} \mathbf{P}(\bigcup_{i=1}^\infty A_i)=\sum_{i=1}^\infty \mathbf{P}(A_i). \end{displaymath}$

[Jos ääretön määrä tapahtumia

on keskenään erillisiä, niin todennäköisyys, että joku tapahtumista

sattuu on sama kuin näiden kaikkien tapahtumien todennäköisyyksien summa.]

Nämä kolme ehtoa ovat ns. Kolmogorovin aksioomat. Viimeisestä aksioomasta eli täydellisestä additiivisuudesta seuraa, että sama on voimassa myös pienemmälle määrälle tapahtumia, eli

Jos $A_i \in \F (i=1,2,\cdots,n)$ ja $A_i \cap A_j=\emptyset$ kaikilla $i \neq j$ , niin

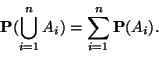
$\begin{displaymath}\mathbf{P}(\bigcup_{i=1}^n A_i)=\sum_{i=1}^n \mathbf{P}(A_i). \end{displaymath}$

[Jos kappaletta tapahtumia on keskenään erillisiä, niin todennäköisyys, että joku tapahtumista sattuu on sama kuin näiden kaikkien tapahtumien todennäköisyyksien summa.]

Nyt olemme saaneet määriteltyä perusjoukon $\Omega$ , $\sigma$ -algebran $\F$ ja todennäköisyyden $\mathbf{P}$ . Kolmikko, johon nämä kaikki kolme kuuluvat $(\Omega, \F, \mathbf{P})$ , on todennäköisyysavaruus.

Tarkastellaan asiaa pienen esimerkin avulla. Tarkastelemme tilannetta, jossa olemme kiinnostuneita, saammeko voiton arpajaisissa. Tapahtuma on voiton saaminen ja sen komplementtitapahtuma, eli tapahtuma, ettemme saa voittoa, on . Olkoon perusjoukko $\Omega$ , tällöin $A \neq \Omega$ ja $A \neq \emptyset$ . $\sigma$ -algebra eli tapahtumien kokooma on $\F=\{\emptyset,A,A^C,\Omega\}$ . Voit tarkastaa, että $\F$ toteuttaa $\sigma$ -algebran ominaisuudet. Jos lisäksi on reaaliluku $0 \leq p\leq 1$ ja $\mathbf{P}$ määritellään seuraavasti
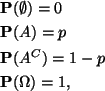
$\begin{align*} &\mathbf{P}(\emptyset)=0 \\ &\mathbf{P}(A)=p\\ &\mathbf{P}(A^C)=1-p\\ &\mathbf{P}(\Omega)=1, \end{align*}$
niin voidaan myös todeta funktion $\mathbf{P}$ toteuttavan todennäköisyysfunktion ominaisuudet.

Nyt olemme käyneet läpi todennäköisyyslaskennan aksioomat ja tästä jatketaan eteenpäin seuraavissa numeroissa.

Bibliography

1

Juve, Y.Todennäköisyyslaskennan alkeet. Suomalaisen kirjallisuuden kirjapaino, Helsinki. 1965.

2

Norlamo, P.,Tuominen, P. Todennäköisyyslaskenta, Osa I. Limes ry, Helsinki. 1974.

3

Tuominen, P. Todennäköisyyslaskenta I. Limes ry, Helsinki. 1990.

Satunnaiskokeen käsitteitä	Merkintä	Todennäköisyysmalli
alkeistapausten joukko	$\Omega$	perusjoukko
alkeistapauksia	$\omega_{1},\omega_{2},...$	perusjoukon alkioita
tapahtumia		joukkoja joiden tn määriteltävissä
kaikkien tapahtumien joukko	$\mathcal{F}$	$\sigma$ -algebra
varma tapahtuma	$\Omega$	perusjoukko
mahdoton tapahtuma	$\emptyset$	tyhjä joukko
tai sattuu	$A \cup B$	yhdiste
ja sattuu	$A \cap B$	leikkaus
ja toisensa poissulkevia	$A\cap B=\emptyset$	tapahtumat ja ovat erillisiä
ei satu	$A^{c}$	joukon komplementti eli $\Omega\setminus A$
sattuu mutta ei satu	$A\setminus B$	joukkoerotus eli $(A\cap B^{c})$
jos sattuu, niin sattuu	$A\subset B$	on joukon osajoukko
ainakin yksi $A_{i}$ sattuu, $i\in\mathbb{N}$	$\overset{\infty}%% {\underset{i=1}{\cup}}A_{i}$	numeroituva yhdiste
kaikki tapahtumat $A_{i}$ sattuvat	$\overset{\infty}{\underset{i=1}{\cap}%% }A_{i}$	numeroituva leikkaus