9. Geometria. Taso ja avaruus

Tavoitteet ja taso

• Tutustutaan erilaisiin kaksi- ja kolmiulotteisiin muotoihin ja joukkoihin.
• Tutkitaan erilaisia geometrisia muotoja: kappaleet -> tasokuviot -> suorat -> piste. Topologisia ominaisuuksia. Monitahokkaat. Monikulmiot.
• Kulma, etäisyys, pituus. Reuna, pinta-ala, lävistäjä. Pinta, pinta-ala, tilavuus.
• Perusominaisuudet ja käsitteet johdatellaan vaiheittain konkreettisista ja tutuista käsitteistä kohti määritelmiä, aksioomia ja teoreemoja. Euklidiset konstruktiot ja todistukset perustuvat geometrisiin kuvauksiin eli transformaatioihin.
• Alemmilla luokilla on hyvin tärkeää käyttää konkreettisia malleja, apuvälineitä, kuvioita, piirroksia - sekä oppilaiden työskentelyssä että demonstraatioissa.
• Jokaiselle oppilaalle on (tarvittaessa kädestä pitäen) opetettava harpin ja viivottimen käyttö.
• Myöhemmin tarvitaan havainnollisuutta uusien käsitteiden tullessa esille. Samanaikaisesti kuitenkin vähennetään visuaalisuuden osuutta ja pyritään aksiomaattista tasoa kohden niille, jotka tulevat jatkamaan matematiikan opintoja yliopistotasolla.
• Yhteydet muihin aloihin (algebra, joukot, funktiot, jne.) ovat myös tärkeitä.

Tarkastellaan geometrisia ongelmia, joissa annettu kuvio on jaettava samanlaisiin osiin:

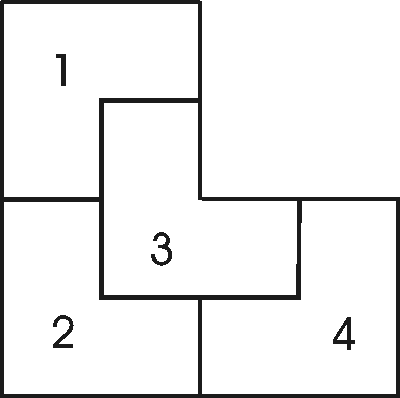
Esim. 1. Kuinka edellä olevassa kuvassa esitetty monikulmio voidaan jakaa neljään samanmuotoiseen ja samankokoiseen osaan?

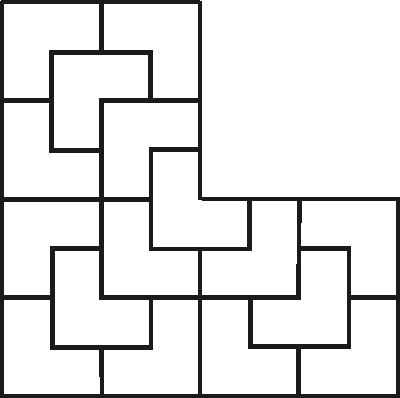
Tehtävä on helpompi ratkaista, jos kuvio piirretään ruudukkoon. Havaitaan, että monikulmion pinta-ala on 12 ruutua, joten voidaan päätellä, että jokaisen osan pinta-alan on vastattava kolmea ruutua. Eräs ratkaisu on esitetty alla vasemmalla olevassa kuvassa. Jatkamalla samaa ideaa saamme monikulmion jaetuksi 16 osaan (alla oikella) ja niin edelleen.

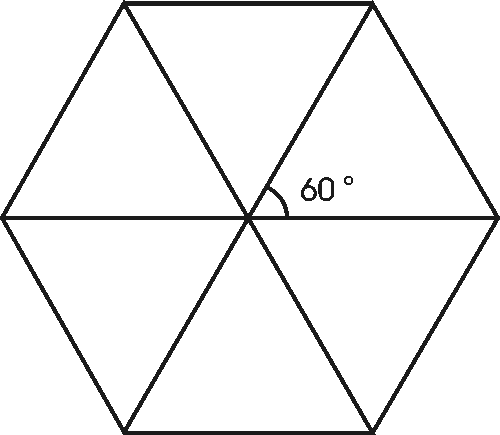
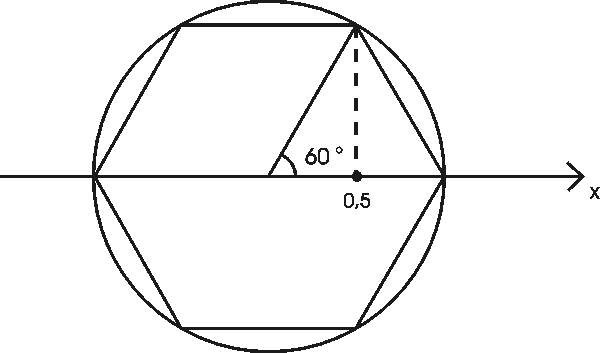
Esim. 2. Seuravaassa tehtävässä tarvitsemme säännöllisen kuusikulmion, joten ensin mietitään miten sellaisen voi piirtää. Kuusikulmio koostuu kuudesta tasakylkisestä kolmiosta (kuva alla vasemmalla). Piirretään ensin koordinaatistoon origokeskinen ympyrä (esim. harpin avulla). Koska cos 60 = 0,5, eräs kuusikulmion kärki sijaitsee ympyräkehän pisteessä, jonka x-koordinaatti on 0,5. Muut kärjet saadaan symmetrian avulla (kuva alla oikealla).

Nyt voimme asettaa varsinaisen ongelman: meidän on jaettava kuusikulmio kahdeksaan samanlaiseen osaan. Tavallinen neliömuotoinen vihkoruudukko ei enää auta, mutta toisentyyppinen - tasasivuinen kolmion muotoinen "ruudukko" auttaa (katso alla oleva kuva). Siinä kuusikulmio on jaettu 24:än pieneen samankokoiseen tasasivuiseen kolmioon. Siis jos haluamme jakaa kuvion kahdeksaan osaan, jokaisen osan pinta-alan on vastattava kolmea kolmiota.

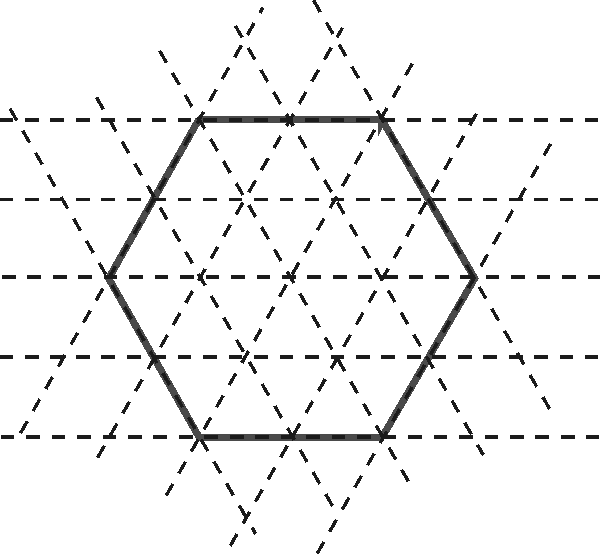
Kaksi tehtävän ratkaisua on piirretty seuraavissa kuvissa.

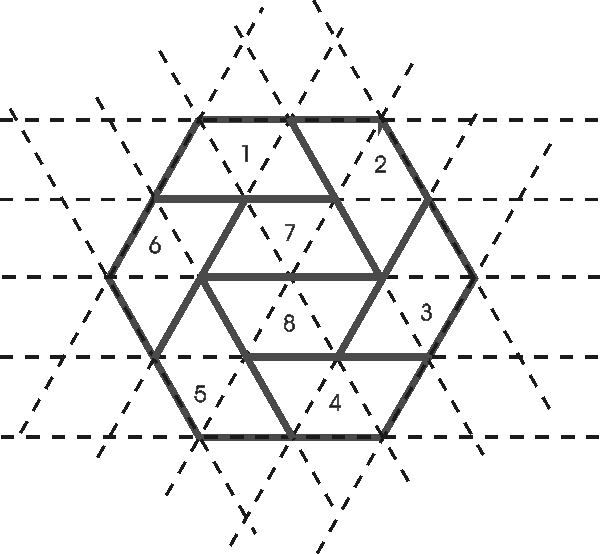Esim. 3. Näiden kahden ongelman jälkeen voimme esittää pienen kompakysymyksen: miten voidaan jakaa annettu suorakulmio yhteentoista osaan? Ratkaisu on selvä - riittää jakaa leveys yhteentoista osaan! Kahden ensimmäisen tehtävän jälkeen oppilas ei välttämättä keksi helppoa vastausta, sillä hän on jo "tottunut" vaikeisiin tehtäviin.

2. Geometrian opiskelu alkaa jo ala-asteella. Tällöin on tärkeintä totutella oppilaat geometriseen maailmaan konkreettisella tasolla. Tärkeimmät aiheet ovat peruskuviot (neliö, kolmio, ympyrä, suorakulmio), suorat, samansuuntaisuus, kohtisuoruus, piiri, suorakulmion pinta-ala, kolmion pinta-ala. Kuvioiden opetus on aloitettava tasokuvioista, sitten siirryttävä avaruuskappalesiin. On tärkeätä näyttää avaruuskappaleet eri kulmista katsottuna, sillä pyrimme kehittämään oppilaiden geometrista hahmotuskykyä.

Jo ala-asteella oppilaille on esittävä mahdollisimman paljon monenlaisia ja monimuotoisia kuvioita, jotta he eivät saa vaikutelmaa, että kaikki kuviot ovat tuttuja, säännöllisiä ympyröitä ja neliötä - alkuvaiheessa kaikki geometriset pistejoukot ovat yhtä kiinnostavia. Yleensäkin matematiikan opetuksessa erilaisia esimerkkejä on oltava runsaasti.

Ala-asteella ei tietenkään ole tarvetta formalisoida geometriaa matemaattisen tarkasti, koska pääpaino on intuitiolla ja konkrettisilla esimerkeillä. Viidennestä vuodesta lähtien aletaan pikkuhiljaa rakentaa teoreettista pohjaa geometriaan.

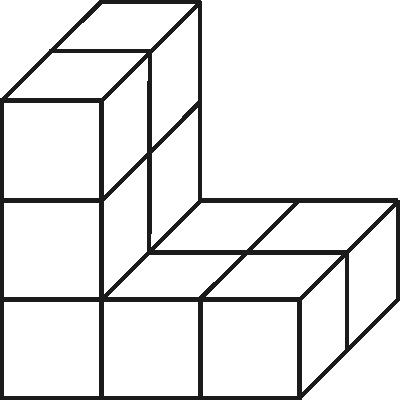
Tutustuminen geometrisiin muotoihin aletaan kolmiulotteisista todellisen elämän esineistä; luokka, televisio jne. Sitten siirrytään tasoon, joka on jo abstraktio (tasolla ja sen osajoukoilla ei ole "paksuutta"). Tutustaan kaikkiin tavallisiin avaruuskappaleisiin, joita ovat esimerkiksi pallo, kuutio, pyramidi, kartio ja prisma. Oppilaille on hyvä antaa esimerkkejä myös monimutkaisemmista kappaleista. On hyödyllistä rakentaa kappaleet yksikkökuutioista (kuva alla vasemmalla). Tällaisten kuvien yhteydessä voimme kysyä kuinka monesta kuutiosta kappale koostuu. Toinen hyvä harjoitus on piirtää kappale eri kulmista; ylhäältä, sivulta jne.

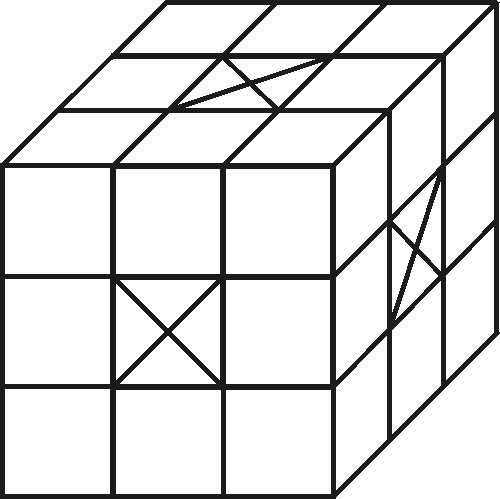Tarkastellaan seuraavaksi esim. kuutiota, jonka sivun pituus on kolme ja joka on siis rakenettu 27 pienestä kuutiosta (kuva yllä oikealla). Otetaan pois neljä kuutiota: keskuskuutio ja kolme muuta, jotka on kuvassa merkitty ristillä. Voidaan kysyä esimerkiksi, mikä on uuden kappaleen tilavuus tai pinta-ala. Tehtävää voi muuttaa vaihtamalla poistettavien kuutioiden määrää ja sijaintia.

Geometrisista malleista

Geometrian opiskelun alkuvaiheessa ovat erittäin tärkeitä oikeat mallit avaruuskappaleista, joita oppilaat yleensä tekevät itse kartongista ja muusta materiaaleista. Ne voivat olla kokonaisia kappaleita tai rautalangasta väännettyjä kappaleiden "luurankoja" (vain särmät). Malleja rakennettaessa on muistettava turvallisuus; malleissa ei saa olla teräviä kulmia. Malleja säilytetään luokassa niitä varten asetetuilla hyllyillä. Malleihin voi liimata paperinpaloja, joihin on kirjoitettu hyödylliset kaavat, esim. kuutioon liittyy kaava V = a³. Sopivien kaavojen yhdistämisen vastaaviin kappaleisiin voi antaa tehtäväksi oppilaille.

Konkreettisia, staattisia malleja tärkeämpiä matematiikassa, erityisesti geometriassa, ovat ei-staattiset, toiminnalliset esimerkit, jotka edustavat muutosta ja liikettä. Geometriassa tällaisiä ovat siirrot, kierrot ja muut yhdenmuotoisuuskuvaukset, kuten suurennokset jne. Oppilaat on opetettava näkemään geometriset muunnokset tasossa ja avaruudessa nimenomaan liikkeenä, reaaliajassa tapahtuvana muutoksena.

Koulugeometriassa on paljon intuitiivisiä käsitteitä, joita ei voi koulussa määritellä, mutta joita meidän on ehdottomasti opetettava. Esimerkiksi piste, suora, taso ovat tällaisia. Voimme vain yrittää havainnollistaa niitä intuition tasolla; "jos pöydän reunasärmä jatkuu äärettömyyteen ja kuvitellaan, ettei sillä ole paksuutta, saadaan suora" jne.

Parissa vuodessa oppilaiden on opittava ymmärtämään monia määrittelemättömiä käsitteitä. Tarkastellaan muutamaa tarkemmin:

Etäisyys

Kysytään ensin oppilailta, mikä on kahden pisteen välinen etäisyys. Suurin osa heistä sanoo, että se on "lyhimmän reitin" pituus, eli pisteiden välisen suoran janan pituus.

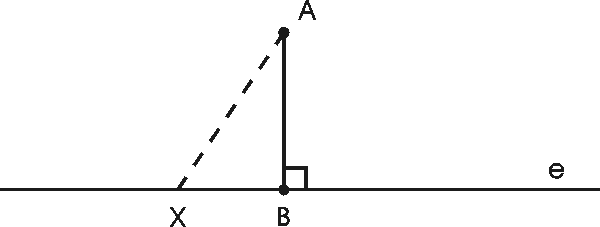
Mikä on sitten pisteen A ja suoran e etäisyys (kuva yllä)? Se on tunnetusti sellaisen janan pituus, joka on kohtisuorassa suoraa vastaan ja kulkee pisteen A kautta. Miksi näin on? Tämä etäisyyshän on vain yksi kaikista mahdollisista etäisyyksistä AX, missä X on suoran piste. Erikoiseksi etäisyyden AB tekee kuitenkin se, että se on pienin kaikista mahdollisista etäisyyksistä. Perustelu on siis jälleen "lyhimmän reitin periaate".

Nyt olemme valmiit määrittelemään tason kahden osajoukon välisen etäisyyden. Se on kuten edellä, pienin kaikista joukkojen pisteparien välisistä etäisyyksistä. Voi tietenkin tapahtua myös niin, että pienintä etäisyyttä ei saavuteta, kuten esim. kahden erillisen avoimen kuulan tapauksessa. Tällöin etäisyys on tunnetusti infimum pisteiden välisistä etäisyyksistä. Koulussa kuitenkin infimumin käsitettä ei esiinny, joten se on selitettävä intuitiivisella tasolla (mitä lukua lähestytään, kun otetaan yhä pienempiä etäisyyksiä pisteparien välillä?). Avointen kuulien tapauksessa voimme myös ensin täydentää kuulat suljetuiksi, mikä ei tunnu vaikuttavan etäisyyteen, ja laskea etäisyyden sen jälkeen.

Kulmat

Jälleen kerran käsite rakennetaan konkreettisin esimerkein; jos pöydällä olevan oppikirjan kantta avataan eri korkeuksille, se muodostaa eri suuruisia kulmia kirjan kanssa. Yksikkönä käytetään alkuvaiheessa asteita, radiaanit otetaan käyttöön myöhemmin trigonometrian yhteydessä. Oppilaan on opittava miten kulmat mitataan eri tilanteissa, esim. mikä on kahden tason välinen kulma, kahden avaruuden suoran, jotka eivät leikkaa, välinen kulma jne.

Ympyrä

Tässä on hyvä esimerkki käsitteestä, joka opetetaan asteittain:

• Ensimmäisessä vaiheessa opettaja piirtää erilaisia kuvioita ja kysyy, mikä niistä on ympyrä. Oppilaan on siis tunnistettava kuvio, mutta hänen ei vielä tarvitse nimetä sitä itse.
• Toisessa vaiheessa oppilaan on osattava nimetä kuvio itse. "Mikä tämä kuvio on? - Se on ympyrä".
• Viidennellä luokalla voimme antaa ympyrän matemaattisen määritelmän: ympyrä on niiden tason pisteiden joukko, jotka sijaitsevat samalla etäisyydellä annetusta tason pisteestä.

Myöhemmin voimme esittää samalla tavalla pallon määritelmän, jossa sana taso on vaihdettu sanaan avaruus.

Geometria viidennestä seitsemänteen luokkaan

Viidentenä vuonna keskitytään seuraaviin aiheesiin: kolmiot, erityisesti suorakulmaiset kolmiot, suorakulmiot, näiden pinta-alat, kuutio, kuution tilavuus ja pinta-ala, ympyrä, ympyrän säde ja kaari. Opetellaan vain konstruktiot, muodot ja peruskäsitteet, matemaattisia ominaisuuksia ja laskuja ei vielä esitetä. Samanlaisuus ja geometriset transformaatiot esitellään leikin avulla, ilman syvällistä matemaattista analyysiä.

Euklidiset konstruktiot (ts. geometriset konstruktiot harpin ja viivottimen avulla) opitaan viidennellä luokalla. Opettajan on varmistettava henkilökohtaisesti, että jokainen oppilas osaa käyttää harppia oikein.

Kuudentena ja seitsemäntenä vuonna puhutaan paljon erilaisista symmetriakuvauksista, peilauksista (akselien suhteen, pisteen suhteen jne.) ja kuvioiden symmetria-akseleista. Opitaan myös erilaiset kulmaparit (komplementtikulmat, suplementtikulmat, eksplementtikulmat). Todistukset ovat tässä vaiheessa visuaalisia ja havainnollisia, kyse on enemmän perusteluista kuin oikeista todistuksista. Todistusten osaamista ei vaadita oppilailta.

Miten geometriset kuvaukset eli transformaatiot on opetettava?

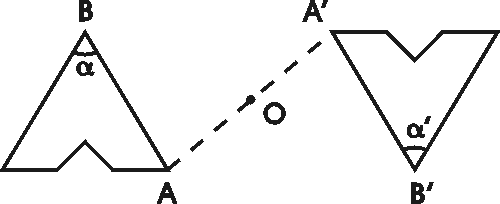
Jälleen kerran, liike on tärkeätä; on osattava nähdä miten kuvio liikkuu tasossa tai avaruudessa ja muuttuu kuvaamisen yhteydessä. Opettaja joutuu itse selittämään ja näyttämään tarkasti miten transformaatio tapahtuu. Esim. alla olevassa kuvassa kuvio (ja taso sen mukana) pyörii 180 astetta pisteen O ympäri, kyseessä on peilaus pisteen O suhteen. Tämän kuvauksen visuaalisen liiketulkinnan jälkeen voimme esittää analyyttisen määritelmän peilaukselle pisteen O suhteen - esim. pisteen A kuva A' saadaan mittaamalla pisteestä O etäisyys OA vektorille OA vastakkaiseen suuntaan.

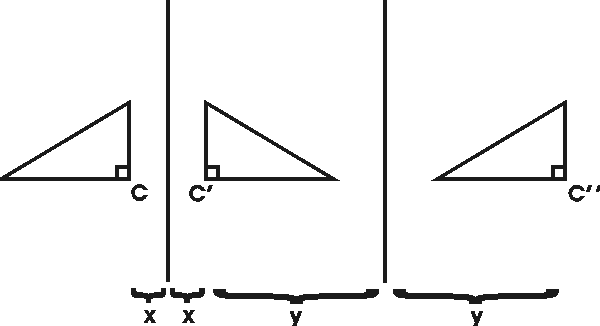
Huomattakoon, että usein vaikka kyse olisi tason osajoukon transformaatiosta, ei ole olemassa muunnoksen tekevää jatkuvaa tason liikettä, vaan kuviota on pyöritettävä sopivasti koko avaruudessa. Esimerkki tällaisesta tilanteesta on peilaus akselin suhteen (kuvat alla), jossa kuvio ikään kuin nousee tasosta ja kääntyy avaruudessa, kunnes aseuttuu takaisin tasoon akselin toiselle puolelle.

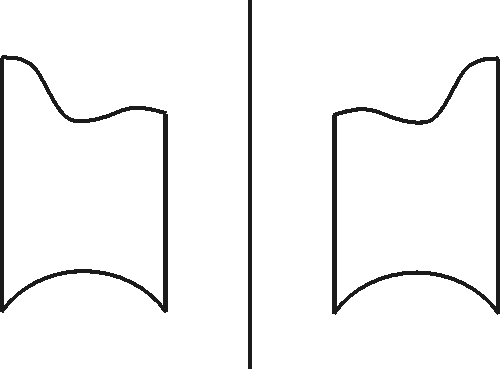On muistettava puhua myös transformaatioiden yhdistämisestä (kuvauksina). Yllä olevassa kuvassa kolmio ensin peilataan akselin suhteen ja sen kuva peilataan taas toisen akselin suhteen (molemmat akselit ovat samansuuntaisia). Kuvassa on x:llä merkitty kolmion kärjen c etäisyys ensimmäisestä akselista ja y:llä sen kuvan ensimmäisessä peilauksessa c' etäisyys toisesta akselista. Kahden peilauksen yhdistetty kuvaus on siis yksinkertaisesti kolmion siirto 2 (x 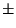y) yksikön verran akseleihin nähden kohtisuoraan suuntaan. Alla olevassa kuvassa on toinen esimerkki kuvausten yhdistämisesta. Kaksi suoraa leikkavat pisteessä M. Kolmio peilataan ensin toisen suoran suhteen, ja kuva peilataan jälleen toisen suoran suhteen. Lopputulos on myös transformaatio; kolmion kierto pisteen M suhteen, missä kiertokulma on suorien välinen kulma kerrottuna kahdella.

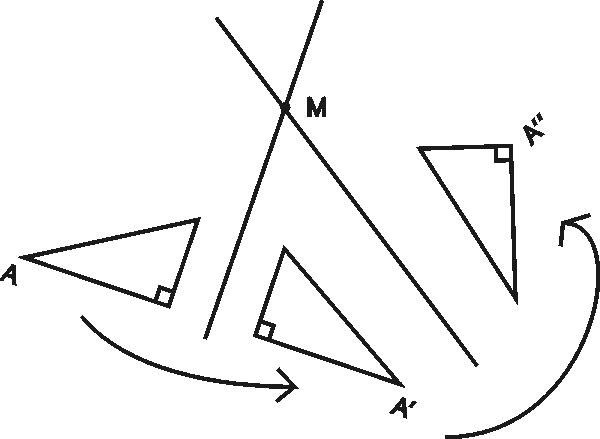
Esimerkki epäeuklidisesta mallista

On hyödyllistä tutustuttaa oppilaat myös epätavalliseen geometriseen maailmaan. Siihen kelpaa mainosti ns. kaupunkiverkkomalli, sillä se on helppo selittää, havainnollinen ja sovelluskelpoinen. Kaupunkiverkostossa pisteet muodostavat diskreetin ruudukkohilan. Ruudukon janat ovat "katuja", joita pitkin pääsee kulkemaan. Kahden pisteen välinen etäisyys kaupunkiverkostomallissa, niin sanottu "taksikuskietäisyys", on lyhin reitti kaupungin katuja pitkin pisteestä toiseen.

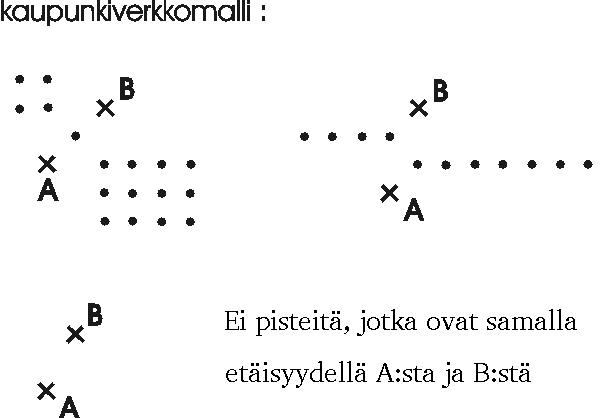
Kaupunkiverkostogeometria poikkeaa tutusta euklidisesta geometriasta monella tavalla. Esimerkiksi, jos A ja B ovat tason kaksi (eri) pistettä, niin niiden pisteiden joukko, jotka sijaitsevat samalla etäisyydellä A:sta ja B:sta on tunnetusti suora, joka on kohtisuorassa janaa AB vastaan ja kulkee sen keskipisteen kautta. Asia on toisin kaupungiverkostossa. Kuvasta näkee, että pisteet, jotka tässä mallissa ovat yhtä kaukana kahdesta kaupungin pisteestä eivät sijaitse samalla suoralla (tavallisessa mielessä). Lisäksi joukon muoto riippuu pisteiden A ja B sijannista toisiinsa nähden. Voi sattua jopa niin, että pisteitä, jotka ovat yhtä kaukana A:sta ja B:sta ei ole olemassa.

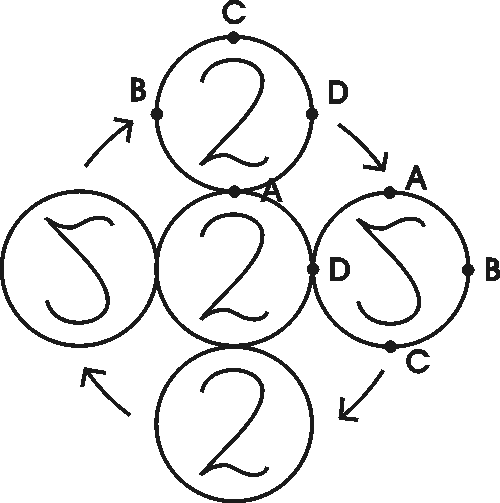
Toinen esimerkki ja hauska leikki on "kolikkogeometria". Otetaan ensin esiin kaksi vaikkapa kahden euron kolikkoa ja laitetaan ne pöydälle, kuten alla vasemmalla olevassa kuvassa. Pidetään alempana oleva kolikko paikallaan ja vieritetään toista kolikkoa sen reunaa pitkin (alla oikella oleva kuva). Kuinka monta kierrosta oman keskipisteensä ympäri liikkuva kolikko ehtii pyörähtää ennenkuin se tekee yhden kierroksen paikalla olevan kolikon ympäri? Helppo koe osoittaa, että kierroksia on 2. Kuvassa on eritelty neljä vaihetta tapahtumasta. Idea voidaan yleistää ottamalla eri kokoisia kolikoita.

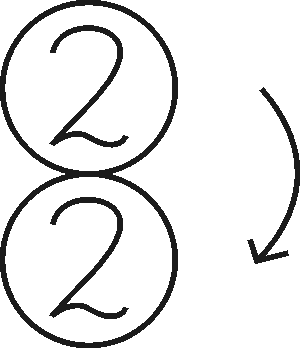Tilavuudesta

Eräs tärkeimmistä koulukurssiin kuuluvista geometrisista kaavoista on pyramidin tilavuuden kaava V = A h / 3, missä A on pohjan pinta-ala, h pyramidin korkeus). Vaikka se on opetettava, sitä ei voi todistaa tarkasti lukuunottamatta erikoistapauksia, kuten suorakulmainen pyramidi. (Tällainen pyramidi on helppoa mahduttaa kuutioon kolme kertaa.) On kuitenkin havainnollisia tapoja perustella kaavaa, esim. mittaamalla, kuinka paljon hiekkaa tai vettä pyramidinmuotoiseen malliin mahtuu.

Koulussa opetetaan myös ilman todistusta Cavalieri-periaate: jos aina kun kaksi kappaletta leikataan kohtisuoralla tasolla syntyvien kuvioiden pinta-alat on samoja, niin kappaleiden tilavuudet ovat myös samoja. Cavalieri-periatteen avulla voidaan todistaa esim. pallon tilavuuden kaava.

Harjoituksia

Oppilaat täydentävät kuvioita opettajan antamien ohjeiden mukaan.

1. Arvioi, mitkä pisteet ovat 2 sentin etäisyydellä annetusta kuviosta (puolisuora, jana, piste, suora, neliö). Näin valmistellaan ympyrän määritelmää.

2. Päättele, mikä kuvio syntyy. Tässä on vastauksia. Keksi kysymykset muihin kuvioihin.

3. Mittaa etäisyyksiä tarkasti.

4. Mieti, millainen tulos tulisi kolmiulotteisessa tapauksessa.

Voidaan myös piirtää kuvioille symmetria-akseleita ja täydentää kuvioita symmetrisesti.

On annettu kaksi pistettä. Mitkä pisteet ovat toisesta etäisyydellä 2 ja toisesta etäisyydellä 3? Vastaus löytyy edellisestä kuvasta.

Geometrisia havainnollistuksia

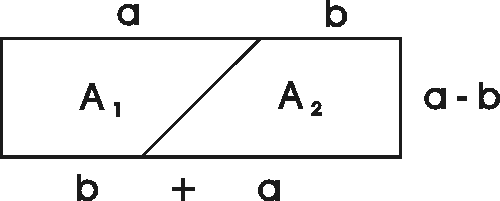
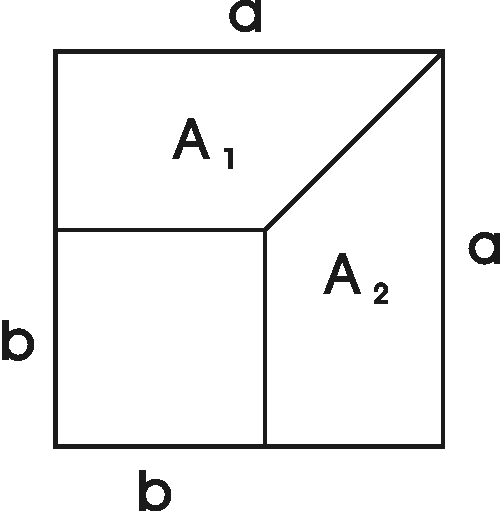
Kaavan A = (a + b)(a - b) = a² - b² havainnollistus pinta-alojen avulla.

Millä tason pisteillä on suorakulmaisessa (x,y)-koordinaatistossa |x| + |y| 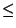1?

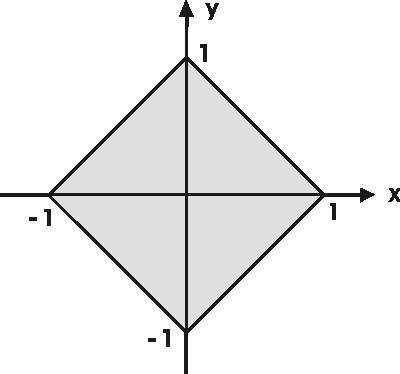
Havainnollistus sarjojen summalle.

1/4 + 1/16 + 1/64 + 1/256 + ...

Jatka seuraavaa kuviota. Laske 17. neliön piiri P₁₇ ja pinta-ala A₁₇.

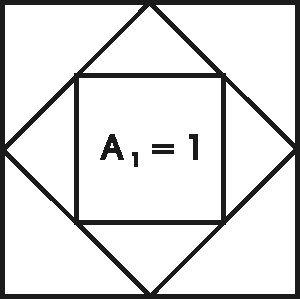
Vastaus:
P₁₇ = 4(2^1/2)¹⁶ = 4 2⁸ = 1024.
A₁₇ = 2¹⁶ = 65536.

Monikulmioita ja muita muotoja

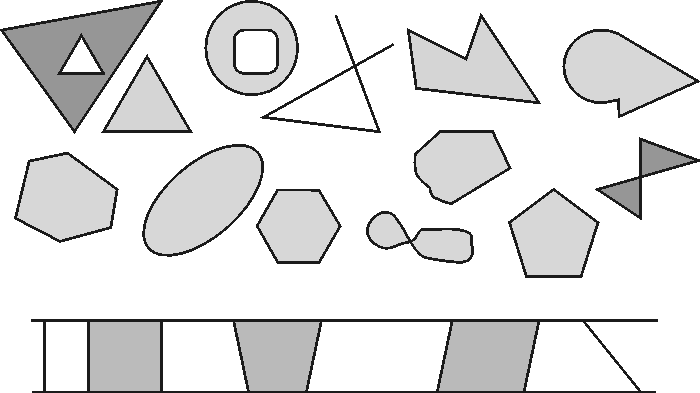
Pituus, kulma, piiri, pinta-ala

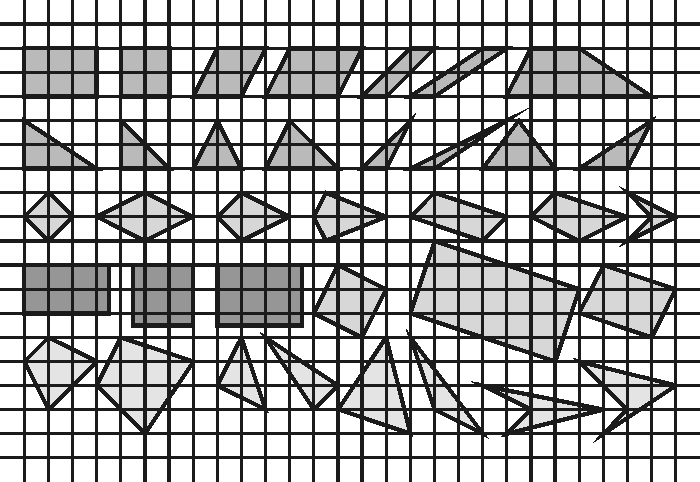
Jos kuvioita piirrettäessä käytetään ruutupaperia, voidaan mitata pinta-alat ja vertailla niitä "leikkaa-liimaa" -menetelmällä (siirretään piirroksessa kuvion osia, joilla on sama pinta-ala).

Montako astetta nämä kulmat ovat? Kuinka pitkiä sivut ovat?

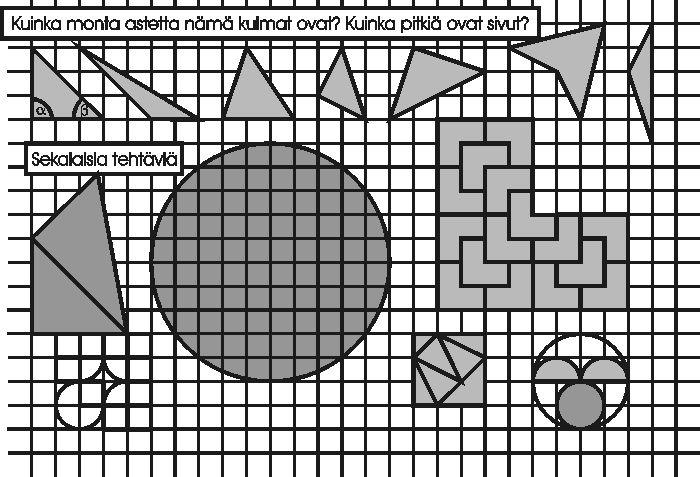
Muita tehtäviä (yllä)

• Oikella oleva kuvio on jaettu 16 yhteneväiseen osaan.
• Piirrä säännöllisiä monikulmioita keskellä olevan ympyräviivan sisälle.
• Laske alhaalla oikella olevan valkoisen osan pinta-ala.
• Pinta-alaan, kulmiin ja yhdenmuotoisiin osiin liittyvissä jakamistehtävissä voidaan käyttää myös tasasivuisten kolmioiden verkkoa:

Tässä on erilaisia tapoja peittää taso yhteneväisillä kuvioilla.

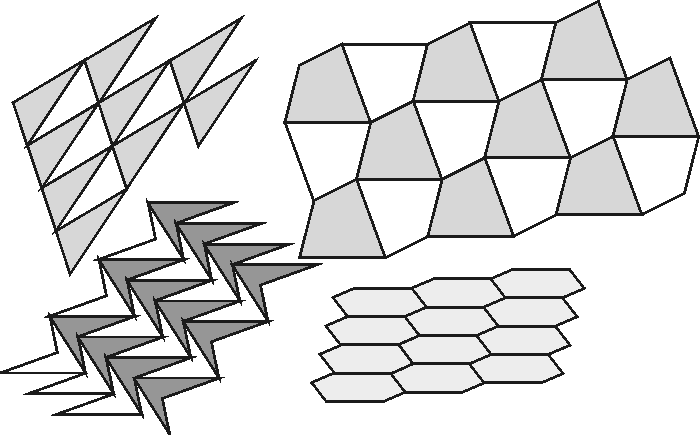
Topologisista muodoista ja homeomorfismiluokista

Tämä aihepiiri antaa mahdollisuuksia käydä hyviä keskusteluja ja saattaa herättää joissakin oppilaissa suurta kiinnostusta matematiikkaa kohtaan. Painokirjainten homeomorfismiluokitusta voidaan muunnella helpoista hyvin monimutkaisiin kysymysasetteluihin. Königsbergin siltaongelma ja siihen liittyvät katkeamattomat viivat ilman reitin toistoa ovat klassisia harjoitustehtäviä - samoin kirjekuorikuvio, viisikulmio lävistäjineen jne. Keskustelun kautta voidaan joidenkin oppilaiden kanssa etsiä sääntöjä:

• jos kuviossa on vain parittomia "kärkikohtia" tai vain yksi parillinen kärki, reitin läpikäynti ilman toistoa ei voi onnistua
• jos kuviossa on kaksi paritonta kärkeä ja muut ovat parillisia, tehtävä onnistuu jos aloittaa toisesta ja lopettaa toiseen parittomaan kärkeen
• jos kuviossa on vain parillisia kärkiä, tehtävä onnistuu aina