Lukualueen laajennusta luonnollisista luvuista kokonaislukuihin (ja edelleen) voidaan havainnollistaa joukko-opillisella kuvalla. Annetaan lukuja ja sijoitetaan ne kuvaan, jossa on sisäkkäisiä joukkoja (luonnolliset luvut, kokonaisluvut, rationaaliluvut, jne.). Sijoittamisen yhteydessä myös perustellaan, miksi kyseinen luku kuuluu juuri tähän joukkoon.
On tärkeää, että ennen kokonaislukujen laskutoimituksia harjoitellaan kokonaisluvun käsitettä monipuolisesti esim. lämpötilojen ja lukusuoran avulla.
Todetaan, että summa pienenee, jos samaan lukuun lisätään pienempi luku. Todetaan, että vähennyslaskun tulos kasvaa, kun samasta luvusta vähennetään pienempi luku.
Puheessa on hyvä tehdä ero laskutoimitusten (+ ja -) ja etumerkkien (+ ja -) välillä.
Yhteen- ja vähennyslaskun opettamisessa voidaan käyttää apuna erilaisia malleja
Laskutoimitusten opettelu aloitetaan yhteenlaskusta. Harjoituksia tarvitaan runsaasti. Yhteenlaskua käytetään vähennyslaskun tuloksen tarkastamiseen. Suositeltava etenemisjärjestys on:
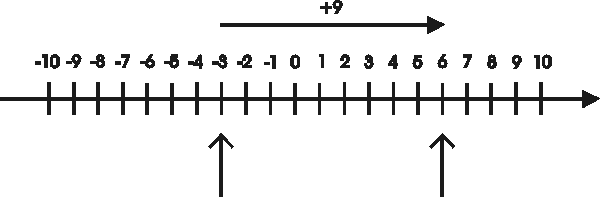
Ensin harjoitellaan positiivisten ja negatiivisten lukujen yhteenlaskua:
Minulla on viisi euroa rahaa, mutta olen velkaa kolme euroa. Paljonko rahaa minulla on?
5 + (-3) = 2
Minulla on kolme euroa käteistä ja viisi euroa velkaa. Mikä on rahatilanteeni?
3 + (-5) = -2
Laske luvut yhteen. -5 + (-3) = -8
Edellisen kuvan tulkinta: minulla on velkaa 5 euroa ja 3 euroa.
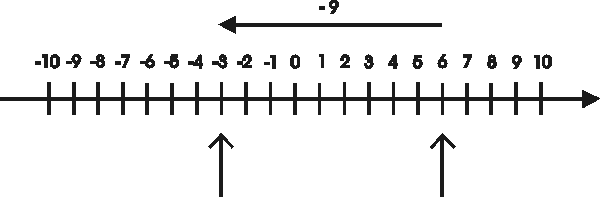
Kaavan 5 - (+3) = 2 havainnollistus:
Sanallinen tulkinta: Käytin käteisestä 5 eurosta 3.
Kaavan -5 - (-3) = -2 havainnollistus:
Sanallinen tulkinta: Maksan 5 euron velasta 3 euroa, velkaa jää 2 euroa.
3 - (+5) = [5 + (-2)] - (+5) = -2. Tässä 3 korvattiin 5 + (-2):lla, siitä poistetaan 5, jää -2.
Tämä on jo vaikea tehtävä: 3 - (-5) = [8 + (-5)] - (-5) = 8. Tässä 3 korvattiin 8 + (-5):llä, siitä poistetaan -5, jää 8.
Kokonaislukujen vähennyslasku lukusuoralla
Voidaan käyttää lämpömittaria tukena.
|
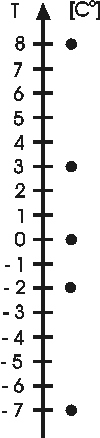
8 on 3:a 5:llä suurempi, siis 8 - 3 = 5. Tarkistus: 5 + 3 = 8.
8 on 0:aa 8:lla suurempi, siis 8 - 0 = 8. Tarkistus: 8 + 0 = 8.
8 on -2:ta 10:llä suurempi, siis 8 - (-2) = 10. Tarkistus: 10 + (-2) = 8.
3 on -2:ta 5:llä suurempi, siis 3 - (-2) = 5. Tarkistus: 5 + (-2) = 3.
0 on -7:ää 7:llä suurempi, siis 0 - (-7) = 7. Tarkistus: 7 + (-7) = 0.
-2 on -7:ää 5:llä suurempi, siis -2 - (-7) = 5. Tarkistus: 5 + (-7) = -2. |
Havaitaan, että jos vähennettävä on suurempi kuin vähentäjä, on erotus positiivinen, ja jos vähennettävä on pienempi kuin vähentäjä, on erotus negatiivinen.
Oppilaat hallitsevat negatiiviset luvut Unkarissa viidennellä luokalla, eli n. 11-vuotiaana.
Toinen tapa käyttää lukusuoraa vähennyslaskussa
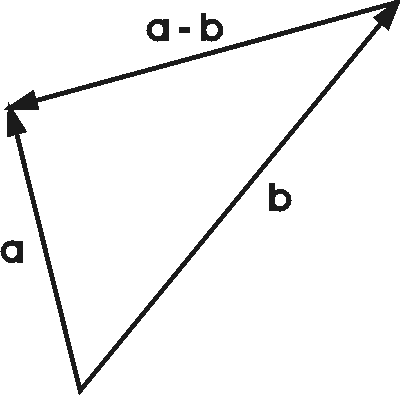
Opettajille voi olla mielenkiintoista huomata tason vektorien yhteen- ja vähennyslaskun analogisuus vastaavaan 1-ulotteiseen tapaukseen, lukusuoran käyttöön kokonaislukujen yhteen- ja vähennyslaskussa.
| 3 + 2 = 5 | -2 + 3 = 1 | 3 - 5 = -2 | -3 - 2 = -5 | 0 - 3 = -3 | ||||
| 3 + 1 = 4 | -2 + 2 = 0 | 3 - 4 = -1 | -3 - 1 = -4 | 0 - 2 = -2 | ||||
| 3 + 0 = 3 | -2 + 1 = -1 | 3 - 3 = 0 | -3 - 0 = -3 | 0 - 1 = -1 | ||||
| 3 + (-1) = 2 | -2 + 0 = -2 | 3 - 2 = 1 | -3 - (-1) = -2 | 0 - 0 = 0 | ||||
| 3 + (-2) = 1 | -2 + (-1) = -3 | 3 - 1 = 2 | -3 - (-2) = -1 | 0 - (-1) = 1 | ||||
| 3 + (-3) = 0 | -2 + (-2) = -4 | 3 - 0 = 3 | -3 - (-3) = 0 | 0 - (-2) = 2 | ||||
| 3 + (-4) = -1 | -2 + (-3) = -5 | 3 - (-1) = 4 | -3 - (-4) = 1 | 0 - (-3) = 3 | ||||
| ... | ... | ... | ... | ... |
3  3 = 9 | (-3) 3 = -9 | |
| 3 2 = 6 | (-3) 2 = -6 | |
| 3 1 = 3 | (-3) 1 = -3 | |
| 3 0 = 0 | (-3) 0 = 0 | |
| 3 (-1) = -3 | (-3) (-1) = 3 | |
| 3 (-2) = -6 | (-3) (-2) = 6 | |
| 3 (-3) = -9 | (-3) (-3) = 9 | |
| ... | ... |
| 8 : 8 = 1 | -15 : 15 = -1 | |
| 8 : 4 = 2 | -15 : 5 = -3 | |
| 8 : 2 = 4 | -15 : 3 = -5 | |
| 8 : 1 = 8 | -15 : 1 = -15 | |
| 8 : (-1) = -8 | -15 : (-1) = 15 | |
| 8 : (-2) = -4 | -15 : (-3) = 5 | |
| 8 : (-4) = -2 | -15 : (-5) = 3 | |
| 8 : (-8) = -1 | -15 : (-15) = 1 | |
| ... | ... |
1. Negatiivisten lukujen summa on niiden itseisarvojen summa "miinusmerkkisenä".
2. Positiivinen ja negatiivinen luku voidaan laskea yhteen niin, että vähennetään pienempi itseisarvo suuremmasta (jos ne eivät ole yhtä suuret) ja etumerkki on itseisarvoltaan suuremman merkki.
3. Luvun vähentäminen on sama asia kuin sen vastaluvun lisääminen.
8 + (-4) - (-5) - (+6) + (+8) + (-12)
= 8 + (-4) + (+5) + (-6) + (+8) + (-12)
= 8 - 4 + 5 - 6 + 8 - 12 = -1.
[8 + 5 + 8 + (-4 - 6 - 12) = 8 + 5 + 8 - (4 + 6 + 12) = 21 - 22 = -1]
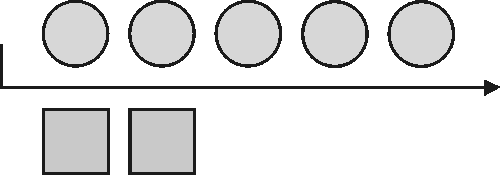
5 4 tarkoittaa: 5 neljästi eli
5 kerrottuna 4:llä [5 + 5 + 5 + 5 = 20]
tai 5 kertaa 4 [4 + 4 + 4 + 4 + 4 = 20]
Tässä on kyseessä valinta: tulkitaanko merkintä
5 4 "5 neljästi" vai "4 viisi kertaa".
Kertolaskun vaihdannaisuuden eli kommutatiivisuuden takia tästä ei tule ongelmaa,
lopputulos on sama.
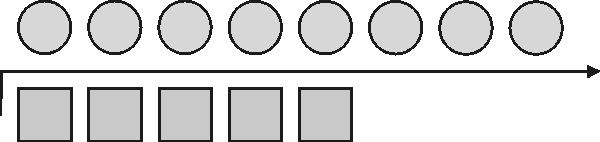
4 (-3) tarkoittaa: 4 kertaa -3
[-3 + (-3) + (-3) + (-3) = -12]
tai 4 kerrottuna -3:lla [4 3:n
vastaluku]
(-4) (-3) tarkoittaa: -4 kertaa -3
[4 kertaa -3:n vastaluku]
tai -4 kerrottuna -3:lla
[-4 3:n vastaluku]