
Yhteenlasku opitaan ala-asteella. Nimityksiä: yhteenlaskettavat, summa. Luonnollisten lukujen yhteenlaskulla on vaihdannaisuus- ja liitännäisyysominaisuus:
Luonnollisten lukujen vähennyslasku opitaan ala-asteella. Nimityksiä: vähennettävä - vähentäjä = erotus.
Päässälasku: 16493 - 7158 = 9493 - 158 = 9343 - 8 = 9335.
Paperilla:
| 16493 |
| - 7158 |
| 9335 |
Tarkistus:
| 9335 |
| + 7158 |
| 16493 |
Luonnollisten lukujen vähennyslaskulla ei ole vaihdannaisuusominaisuutta,
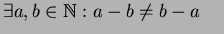 lisäksi
lisäksi
 |
Kahden luonnollisen luvun erotus on luonnollinen luku jos ja vain jos vähennettävä on suurempi tai yhtä suuri luku kuin vähentäjä.
Luonnollisten lukujen kertolasku opitaan ala-asteella. Nimityksiä: tulon tekijät, kerrottava, kertoja, tulo.
![]()
(45 kerrottuna 12:lla on 540)
(45 kertaa 12 on 540)
Luonnollisten lukujen kertolaskulla on vaihdannaisuus- ja liitännäisyysominaisuus:
Minkä tahansa kahden luonnollisen luvun tulo on luonnollinen luku.
Kertolaskulla on ositteluominaisuus yhteenlaskun/vähennyslaskun suhteen. Tästä seuraa, että summa tai erotus voidaan kertoa termeittäin ja toisaalta termien yhteinen tekijä voidaan ottaa ulos suluista.
Jakolasku. Nimityksiä: Jaettava : jakaja = osamäärä (ja mahdollinen
jakojäännös). Jaettava = jakaja ![]() osamäärä + jakojäännös.
osamäärä + jakojäännös.
Esimerkki: 26485 : 307 = 86 kokonaista, jakojäännös on 83.
Tarkastus: 307 ![]() 86 = 26402 ja 26402 + 83 = 26485.
86 = 26402 ja 26402 + 83 = 26485.
Kahden nollasta poikkeavan luonnollisen luvun osamäärä on luonnollinen luku jos ja vain jos jaettava on jakajan (kokonaisluku) monikerta.
![]() jos
jos ![]() .
.
Nollalla jakamista ei voida määritellä.
Oppilaille voisi perustella kahdella tavalla, että nolla ei voi olla jakaja.
1. tapa. Annetaan oppilaille tehtäväksi miettiä, mitä on 5 : 0.
Oppilaat voivat antaa hyvin erilaisia vastauksia (0, 5, 1, 7...),
joita sitten tarkastellaan.
Esim. jos 5 : 0 olisi 5, niin tarkistus antaisi
![]() .
Vastaavasti kävisi muille luvuille.
Joku voi kysyä, mitä on 0 : 0. Kaikilla
.
Vastaavasti kävisi muille luvuille.
Joku voi kysyä, mitä on 0 : 0. Kaikilla
![]() on
on
![]() , mutta
nollalla ei voi tässäkään tapauksessa jakaa, koska tuloksena pitäisi
olla vain yksi luku.
, mutta
nollalla ei voi tässäkään tapauksessa jakaa, koska tuloksena pitäisi
olla vain yksi luku.
2. tapa.
5 : 5 = 1
5 : 1 = 5
5 : 1/2 = 10
5 : 1/10 = 50 jne.
Todetaan, että osamäärät kasvavat/pienenevät (koska 5 : (-5) = -1 jne.) rajatta.
Luonnolliset luvut, tehtäviä
1. Sanotaan, että luonnollinen luku, jonka numerot kasvavat, on "mielenkiintoinen" (esimerkiksi 123 tai 489). Vastaavasti nimetään luonnolliset luvut, joiden numerot vähenevät, "hauskoiksi". Kuinka monta 3-numeroista mielenkiintoista (hauskaa) luonnollista lukua on olemassa?
Vastaus.
(7 + 6 + 5 + 4 + 3 + 2 + 1) + (6 + 5 + 4 + 3 + 2 + 1) + ... + (2 + 1) + 1 = 84.
(8 + 7 + 6 + 5 + 4 + 3 + 2 + 1) + (7 + 6 + 5 + 4 + 3 + 2 + 1) + ... + (2 + 1) + 1 = 120.
2. Poista luvusta 123456789101112131415 kymmenen numeroa siten, että jäljelle jäävät numerot tässä järjestyksessä antavat mahdollisimman pienen/suuren luvun.
Vastaus. 10111131415, 91112131415.
3. Toisen maailmansodan jälkeen vuonna 1946 tapahtui Unkarissa "pengön"
devalvaatio. Yksi uusi forintti oli arvoltaan
![]() pengöä. Kuinka monta nollaa on tässä luvussa numeron neljä jälkeen?
pengöä. Kuinka monta nollaa on tässä luvussa numeron neljä jälkeen?
Vastaus. 29.
Miljoona on ![]() , tuhat kertaa miljoona on miljardi (engl. billion)
, tuhat kertaa miljoona on miljardi (engl. billion)
![]() .
.
Vaativampia tehtäviä
1. Anna kirjaimille lukuarvot.
SEND + MORE ------ MONEY
Vastaus. D = 7, E = 5, M = 1, N = 6, O = 0, R = 8, S = 9, Y =2.
2. Onko olemassa numeroon 2 loppuvaa luonnollista lukua, jolle on voimassa: kun viimeinen numero siirretään luvun alkuun, saadaan alkuperäinen luku kaksinkertaisena?
Vastaus. Tällainen luku on olemassa, se on 105263157894736842.
3. Todista, että kaikkien luonnolllisten lukujen seitsemännen ja kolmannen potenssin viimeinen numero on sama.
Ratkaisu.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
4. Kirjoita seuraava suure normaalissa muodossa. Maan massa on noin 6 000 000 000 000 000 000 000 tonnia.
Vastaus.
![]() .
.
5. Pitkä laiva seilaa joella. Toni kävelee rannalla laivan perästä keulaan 400 askeleella. Toni kävelee 100 askelta takaisinpäin ja on jälleen laivan perän kohdalla. Kuinka monta askelta pitkä laiva on?
Vastaus. 160 askelta.
6. Aloitamme kirjoittamaan luonnollisia lukuja perätysten: 123456789101112131415161718... Mikä numero on 2002:lla paikalla?
Vastaus. 3.
Lisää tehtäviä
1. Kumpi on suurempi, ![]() vai
vai ![]() ? (
? (
![]() )
)
![]() vai
vai ![]() ? (
? (
![]() )
)
2. Ratkaise epäyhtälöt luonnollisten lukujen joukossa.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
(![]() )
)
3. Koulussa on 400 oppilasta. Onko heistä kahdella varmasti sama syntymäpäivä?
Vastaus: Kyllä. Riittää, että oppilaita on 367.
4. Shakkipelin keksijä pyysi shaahilta yhden viljanjyvän ensimmäiseen ruutuun, 2 toiseen, 4 kolmanteen, 8 neljänteen ja niin edelleen. Pystyikö shaahi toteuttamaan pyynnön?
![]()
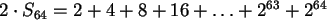
Vähentämällä saadaan, että 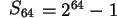 .
.
16 vehnänjyvää painaa noin gramman. Nykyisin maailmassa tuotetaan
noin
![]() tonnia vehnää vuodessa.
tonnia vehnää vuodessa.
![]()