2. Joukko-oppia ja logiikkaa

Tavoitteet, taso ja sisältö

• Tavoite: Yhteisen, yleisen perustan luominen eri matematiikan osa-alueille.
• Puhutun kielen loogisten elementtien riittävä oppiminen ja käyttö, sekä soveltaminen eri matematiikan alueilla.
• Aksiooman, määritelmän ja teoreeman merkitysten oppiminen.
• Rauhallinen, matemaattista joukko-oppia ja matemaattista logiikkaa kohti johtava kehitys.
• Taso: Alle 14-vuotiaille opetetaan konkreettisilla käsitteillä ja esimerkeillä, joissa ei ole abstrakteja merkkejä. Symbolien käyttöä opetetaan asteittain vanhemmille oppilaille. Symboleita voi opettaa joillekin lapsille ennen yläastetta, mutta se ei ole välttämätöntä.
• Sisältö: Joukkojen ja logiikoiden operaatiot (kuten JA, TAI sekä JOS-NIIN). Joukkojen relaatiot ($\subseteq$ ja $\subset$), kaaviot (Venn ja Carol), pistejoukot ja loogiset kvanttorit.

Määritelmiä

Joukko A on sama kuin joukko B, jos niiden alkiot ovat samat (A = B).

Joukko A on joukon B osajoukko, jos siitä, että x $\in$ A seuraa x $\in$ B (A $\subseteq$ B).

A:n komplementti CA on niiden perusjoukon alkioiden joukko, joille x 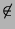A.

Joukko A on joukon B aito osajoukko, jos A $\subseteq$ B ja A $\neq$ B.

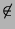Joukkojen A ja B joukko-opillinen erotus A \ B = {x $\in$ ja x B}.

Määritelmän mukaan A X B on järjestettyjen parien (x,y) joukko, jossa x $\in$ A ja y $\in$ B (A X B := {(x,y) | x $\in$ A, y $\in$ B}).

Kutsumme joukkoa $\rho$ relaatioksi joukkojen A ja B välillä, jos $\rho\subseteq$ A X B.

Reaaliluvuilta reaaliluvuille -funktioita kutsutaan yhden muuttujan reaalifunktioiksi.

Yhden muuttujan reaalifunktioita joukosta (Z+ = {1,2,3...}) kutsutaan jonoksi.

• Annetaan kaksi tason suoraa e ja f. Minkä joukon muodostavat ne tason (avaruuden) pisteet, jotka ovat yhtä etäällä suorista e ja f?
• Minkä joukon muodostavat pisteet, jotka ovat 2 cm etäisyydellä 5 cm pitkästä janasta tasossa (avaruudessa)?

Menetelmät, ideat ja esimerkit

Joukkojen leikkaukset ja yhdisteet sekä JA ja TAI

Puhutussa kielessä JA konnektiivia käytetään merkityksissä "samanaikaisesti" ja "ja myös". Käytämme sanaa TAI sekä molemmat sallivassa ("toinen tai molemmat") että poissulkevassa ("vain jompikumpi") merkityksessä. Tämä käytäntö poikkeaa loogisesta merkityksestä, koska looginen TAI on pelkästään molemmat salliva.

A $\cap$ B = {sekä 15:n että 20:n jakajat}

A $\cup$ B = {15:n tai 20:n jakajat}

Tällaisia esimerkkejä voi ottaa, jos luokan oppilailla on jo jonkin verran verran kokemusta konkreettisista joukoista ja Venn-kaavioista (Unkarissa n. 11-vuotiaat). On havaittu, että oppilaat pystyvät muodostamaan tai esittämään kahden yksinkertaisen (konkreettisen) joukon yhteisen osan (leikkauksen) ongelmitta. On kuitenkin tavallista, että he eivät osaa muodostaa tai esittää näiden joukkojen yhdistettä.

Tarkastellaan tätä ongelmaa kaaviossa:

Opettaja: Mikä ominaisuus on niillä alkioilla, jotka ovat joukkojen A ja B yhteisessä osassa?

Oppilas 1: Siellä ovat ne luvut, jotka ovat 15 ja 20 jakajat.

Opettajan olisi hyvä kysyä: Samanaikaisestiko? Ja oppilaiden: Kyllä, samanaikaisesti.

Oppilas 2: Luvut jotka jakavat sekä 15 että 20 ilman jakojäännöstä.

Oppilas 3: Luvut jotka jakavat 15 ilman jakojäännöstä mutta myös 20 ilman jakojäännöstä.

Opettaja: Mikä ominaisuus on niillä alkioilla jotka ovat joukkojen A ja B yhdisteessä?

Oppilas 1: 15 ja 20 jakajat [Ei pidä paikkaansa!]

Opettajan olisi kysyttävä: "Mitä tarkoitat? Samanaikaisestiko?" Oppilaiden vastata: "Ei."

Oppilas 2: 15:n jakajat ja 20:n jakajat. [Ei pidä paikkaansa!]

Opettajan olisi kysyttävä: "Samanaikaisestiko? Molempien jakajat?" Oppilaiden vastata: "Ei. 15:n jakajat ja myös 20:n jakajat." Opettaja: Matematiikassa sanotaan: 15:n tai 20:n jakajat."

Opettaja esittää tämän jälkeen loogisen (molemmat sallivan) TAI:n merkityksen: "Ne luvut, jotka jakavat ainakin yhden luvuista 15 ja 20."

Esimerkki

Tässä on eräs idea molemmat sallivan "tain" opettamiseen:

Opettaja: Äiti sanoi isälle: Syömme tänään päivällistä, jos Salli tai Kalle käy ostamassa ruokaa sitä varten. Missä tapauksissa perhe saa tänään päivällisensä?

Oppilaat: Jos Salli käy yksin ostamassa ruokaa. Jos Kalle käy yksin ostamassa ruokaa. Ja jos molemmat lapset käyvät ostamassa ruokaa. (Jos ainakin toinen heistä käy ostamassa ruokaa.)

Esimerkki

Olemme merkinneet ryhmän viidennen luokan oppilaita tähän joukkokaavioon.

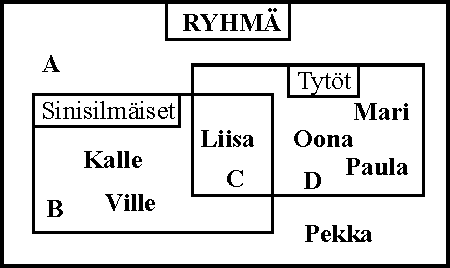
A = {Oppilaat, jotka eivät ole sinisilmäisiä eivätkä tyttöjä}

B = {Sinisilmäiset oppilaat, jotka eivät ole tyttöjä}

C = {Luokan sinisilmäiset tytöt}

D = {Luokalla olevat tytöt, jotka eivät ole sinisilmäisiä}

Kuvan mukaan

{sinisilmäiset} $\cap$ {tytöt} = {Liisa}

{sinisilmäiset} $\cup$ {tytöt} = {Kalle, Ville, Liisa, Oona, Mari, Paula}

{sinisilmäiset} \ {tytöt} = {Kalle, Ville}

{tytöt} \ {sinisilmäiset} = {Mari, Oona, Paula}

Kuvan perusteella voidaan työskennellä vaikka näin:

Aloittava kysymys (itsenäistä työskentelyä - keskustelua luokan kesken):

Opettaja: Olemme merkinneet ryhmän viidennen luokan oppilaita tähän joukkokaavioon. Luettele ne lapset jotka

(1) ovat tyttöjä ja sinisilmäisiä.

(2) ovat tyttöjä tai ovat sinisilmäisiä.

Keskustelussa tarkastellaan "ja" ja "tai" -sanojen käyttöä. Tämä on ensimmäinen mahdollisuus asioiden selkeytymiselle ja yhteisymmärrykselle. Opettaja käyttää ilmaisuja "yhteinen osa" tai "leikkaus" kuten myös "yhdistelmä" tai "yhdiste".

(3) ovat sinisilmäisiä ja eivät ole tyttöjä. Keskustelussa opettaja saa palautetta siitä, ovatko käsitteet selkeytyneet.

(4) Kirjoita mitkä alkiot kuuluvat osaan A; B; C ja D. Keskustelu: Voimme myös tarkkailla ketkä tarvitsevat näyttämistä. Toivomme, että jotkin lapsista huomaavat yhteyden C:n ja (1):n sekä B:n ja (3):n välillä sekä nimien käytön.

(5) Kirjoita niiden oppilaiden yhteiset ominaisuudet, joiden nimet on kirjoitettu B:n C:n ja D:n yhdisteeseen. Keskustelu: Voimme tarkastella sanojen "yhdistelmä" ja "yhdiste" ymmärtämystä sekä sitä, millä tasolla oppilaiden sanojen käyttö on. Kohtien (2) ja (5) välistä yhteyttä eivät oppilaat todennäköisesti mainitse.

(6) Kirjoita kuinka monta alkiota joukossa B; C; D; "sinisilmäiset" ja "tytöt" on?

(7) kirjoita kuinka monta alkiota on joukkojen "sinisilmäiset" ja "tytöt" yhdisteessä? Keskustelu: Toivomme oppilaiden huomaavan ristiriidan 3 + 4 = 6. Huomaa yhteys (2):n, (5):n ja (7):n välillä.

Arkikielen monimerkityksinen "ja" voi aiheuttaa sekaannuksia kahden joukon yhdistettä muodostettaessa. Toisin sanoen: Osa oppilaista määrittelee joukon "sinisilmäiset" $\cup$ "tytöt" joukkona "sinisilmäiset ja tytöt". He siis käyttävät "luetteloivaa ja:ta" (ja myös) kun heidän pitäisi käyttää oikeastaan "tai":ta. Opettajan on syytä olla kärsivällinen, mutta myös osoittaa oppilaille tämä monimerkityksellisyys. Siis korjatkaamme heitä ja käyttäkäämme itse jatkuvasti oikeita ilmaisuja. Siis: Joukkojen A ja B yhdiste A $\cup$ B on ne oppilaat, jotka ovat tyttöjä tai sinisilmäisiä, eivät ne oppilaat, jotka ovat tyttöjä ja sinisilmäisiä.

Kolmioiden ja nelikulmioiden luokittelu

1. Kolmioiden luokittelu.

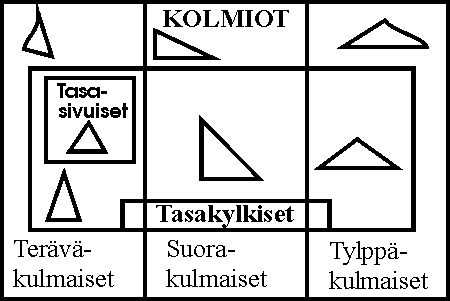
2. Piirrä ainakin yksi sovelias nelikulmio kuhunkin joukkoon.

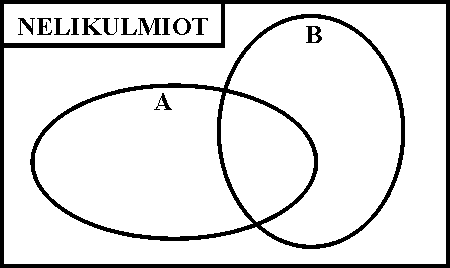
a) A = {nelikulmion kaksi sivua ovat saman suuntaiset} B = {nelikulmiolla on symmetria-akseli}

b) A = {nelikulmion vastakkaiset sivut ovat samanpituiset} B = {nelikulmion vastakkaiset sivut ovat samansuuntaiset}

c) A = {nelikulmion kaikki sivut ovat samanpituiset} B = {nelikulmion kaikki kulmat ovat saman suuruiset}

d) A = {nelikulmio on kovera} B = {nelikulmio ei ole kovera}

e) A = {nelikulmio on suunnikas} B = {nelikulmiolla on suora kulma}

f) A = {nelikulmio on kovera} B = {nelikulmio on symmetria-akseli}

g) A = {nelikulmio on suunnikas} B = {nelikulmio on vinoneliö}

h) A = {nelikulmio on suunnikas} B = {nelikulmio on suorakulmio}

3. Kirjoita sopiva kirjain kuhunkin kohtaan.

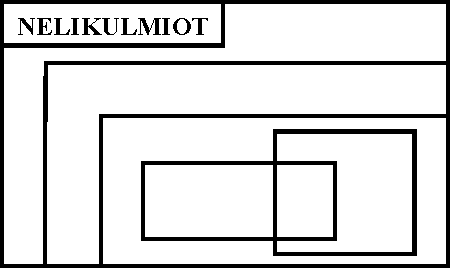
A = {puolisuunnikkaat} B = {suorakulmiot} C = {vinoneliöt} D = {neliöt} E = {suunnikkaat}

Vastaus.

4. Piirrä ainakin yksi nelikulmio jokaiseen kohtaan. Väritä ne osat, joissa ei ole alkioita. A = {suorakulmiot} B = {vinoneliöt} C = {neliöt}

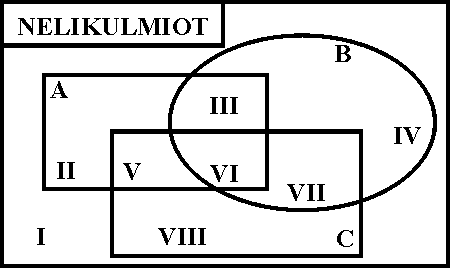
Esimerkki

Joukko-opin avulla voidaan esittää lukujen jaollisuutta.

1. Esimerkkejä jaollisuudesta.

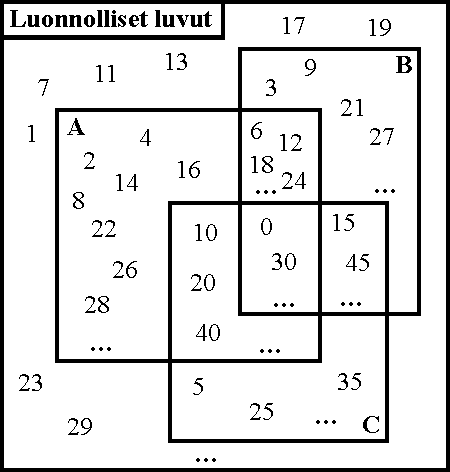
Yllä olevassa kuvassa on:

A = {2:n monikerrat} B = {3:n monikerrat} C = {5:n monikerrat}

Sijoita nämä joukot vastaavasti:

a) A₁ = {4:n monikerrat} B₁ = {6:n monikerrat} C₁ = {9:n monikerrat}

b) A₂ = {2:n monikerrat} B₂ = {3:n monikerrat} C₂ = {4:n monikerrat}

c) A₃ = {2:n monikerrat} B₂ = {4:n monikerrat} C₃ = {8:n monikerrat}

2. Kuinka moneen (keskenään erilliseen) osaan on esimerkkien 1, 2, 3 Venn-kaavioiden kuvat jaettu? [8;6;4]

Kuinka monta joukkoa voidaan löytää esimerkkien 1, 2, 3 Venn-kaavioista? [2 potenssiin 8 = 256; 2 potenssiin 6 = 64; 2 potenssiin 4 = 16] (Näitä tehtäviä voi antaa oppilaille kahdeksannen luokan jälkeen.)

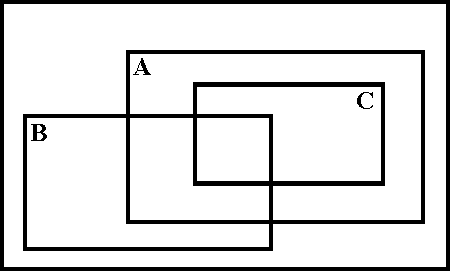
3. Järjestetään nelikulmiot ensimmäisen kaltaisessa Venn-kaaviossa, jos joukot ovat: A = {nelikulmiolla on symmetria-akseli, joka kulkee kärjen kautta} B = {nelikulmiolla on symmetria-akseli, joka kulkee sivun keskipisteen läpi} C = {nelikulmiolla on symmetriakeskus}

4. Järjestetään nelikulmiot kolmannen kaltaisessa Venn-kaaviossa, jos joukot ovat: A = {nelikulmiolla on symmetriakeskus} B = {nelikulmiolla on vähintään kaksi symmetria-akselia} C = {nelikulmiolla on 4 symmetria-akselia}

5. Luettele joukot, jotka voidaan tunnistaa tästä Venn-kaaviosta:

Kahden joukon A, B ja perusjoukon E tapauksessa:
$\emptyset$, E,
A, B,
CA, CB,
A $\cap$ B, C(A $\cap$ B),
A $\cup$ B, C(A $\cup$ B),
A $\setminus$ B, C(A $\setminus$ B),
B $\setminus$ A, C(B $\setminus$ A),
(A $\setminus$ B) $\cup$ (B $\setminus$ A), C((A $\setminus$ B) $\cup$ (B $\setminus$ A)).

6. Kuinka monta positiivista kokonaislukua, jotka eivät ole jaollisia millään luvuista 2, 3 ja 5, on välillä [1,1000]?

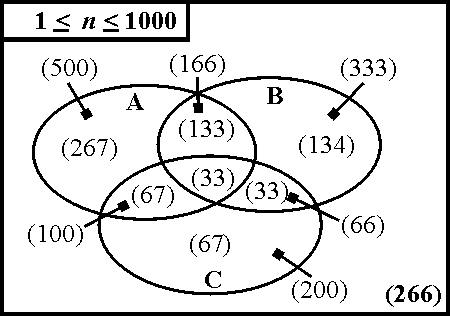
Tässä A on kahdella jaollisten lukujen joukko, B 3:lla ja C 5:llä.

|A $\cup$ B $\cup$ C| = |A| + |B| + |C| - (|A $\cap$ B| + |A $\cap$ C| + |B $\cap$ C| + |A $\cap$ B $\cap$ C| = 500 + 333 + 200 - (100 + 166 + 66) + 33 = 1033 - 332 + 33 = 734.

1000 - 734 = 266.

Esimerkkejä lukiotasolta joukko-opin käytöstä

1. Piirrä karteesisen koordinaatiston pisteet P(x,y), jotka täyttävät ehdon |x| + |y| < 1.

Ratkaisu:

Jos x > 0 ja y > 0, niin x + y < 1, joten y < -x + 1.

Jos x > 0 ja y < 0, niin x - y < 1, joten y > x - 1.

Jos x < 0 ja y > 0, niin -x + y < 1, joten y < x + 1.

Jos x < 0 ja y < 0, niin -x - y < 1, joten y > -x - 1.

Neljä epäyhtälöä antavat vastaukseksi neliön ilman reunoja, jolla on kulmapisteinä (1,0), (0,1), (-1,0) ja (0,-1).

2. Olkoon M epäyhtälön $x^2+y^2\le 5$ ratkaisujoukko joukossa R x R. Kuinka monta alkiota on joukossa M $\cap$ (Z x Z)?

3. Määrittele A $\cap$ B ja A $\cup$ B, jos A = {x $\in$ R | 0 $\ge$ $x^2$ + 2x - 4} ja B = {x $\in$ R | 0 $x^2$ + 4x - 1}.

4. Onko kaikille joukoille A ja B totta, että ((A $\setminus$ B) $\cup$ (B $\setminus$ A)) $\subset$ A $\cup$ B?

5. Kuinka monta 3:n alkion osajoukkoa on 10:n alkion joukossa? Kuinka monta 2:n alkion osajoukkoa on 10:n alkion joukossa?

Tämä tehtävä on yhtälailla kombinatoriikkaa kuin joukko-oppia.

6. Olkoon H kaikkien 1000:tta pienempien positiivisten kokonaislukujen joukko. Kuinka monta alkiota on kaikkien H:n osajoukkojen kokoelmassa?

Esimerkkejä logiikasta

1. Temppu: Osoitetaan, että 3 = 5.

Vähennetään 4 molemmilta puolilta.

-1 = 1 korotetaan molemmat puolet toiseen potenssiin.

1 = 1 mikä on totta. Missä on virhe?

Huomautus: Emme osoittaneet että 3 = 5, mutta osoitimme, että väärästä väitteestä seuraa sallituilla askelilla tosia väitteitä.

"Jos-niin" implikaatio on ongelmallinen. Vaikka logiikka on opintosuunnitelmassa jo ala-asteelta, ei kouluissa selitetä, että implikaatio on tosi aina, kun ensimmäinen jäsen on epätosi.

2. Jos 5 = 5, niin 7 = 7. Tämä on tosi implikaatio (määritelmän mukaan).

Jos 1 = 1, niin 3 = 5. Epätosi implikaatio (määritelmän mukaan).

Jos 3 = 5, niin 1 = 1. Tosi implikaatio (määritelmän mukaan).

Jos 3 = 5, niin 9 = 2. Tosi implikaatio (määritelmän mukaan).

3. Implikaation ja ekvivalenssin totuustaulukot voidaan katsoa kuvasta.

Muistisääntö: Implikaatio ei salli epätotta johdettavan todesta.

Ekvivalenssin määritelmä: "A jos ja vain jos B." "Jos A niin silloin ja vain silloin B" ja "A täsmälleen silloin, kun B."

Peruskoulussa ei kuitenkaan opeteta näitä määritelmiä. Siellä pidättäydytään konkreettisissa väitteissä.