
1. Matematiikan opettamisesta
Matematiikan osaamistason mittaaminen
Tri Tíbor Szalontai on unkarilainen matematiikan didaktikko. Hänen
toimipaikkansa on Institute of Mathematics and Informatics, The
College of Nyiregyháza. Szalontai on tehnyt jo useita vuosia
yhteistyötä englantilaisen prof. David Burghesin ryhmän kanssa
(Centre for Innovation in Mathematics Teaching (CIMT), University of
Exeter, U.K.) ja sovittanut Englannissa tehtävää matematiikan
opetuskokeilua varten Sandor Hajdun oppikirjojen pohjalta
oppimateriaalit.
Szalontai kertoi suomalaisten ja unkarilaisten lasten
menestyksestä matematiikan osaamistason
kansainvälisissä vertailuissa. Vuoden 1991 IMAP kartoituksessa
Unkari ja Sveitsi olivat parhaat osallistuneista Euroopan maista.
Vuonna 1995 TIMSS-tutkimuksessa Unkari sijoittui sijalle 14, jota
Szalontai ei pitänyt kovin hyvänä sijoituksena.
Vuonna 1999 Unkari ylsi sijalle 9 ja Suomi sijalle 20. Uusimmassa
Pisa-tutkimuksessa (mukana 31 maata) Suomi sijoittui ensimmäiseksi.
Kyseistä tutkimusta on kuitenkin kritisoitu siitä, että se mittasi
enemmän luetun ymmärtämistä ja lukutaitoa kuin matematiikan
hallitsemista. Tämä kritiikki on
sopusoinnussa sen kanssa, että suomalaiset ovat tutkimuksissa menestyneet parhaiten
lukutaidossa.
Szalontai puhui myös eriyttämisestä koulujärjestelmässä.
Eriyttää voidaan mm. antamalla erilaisia kotitehtäviä.
Opettaja voi määrätä tehtävät, mutta
Szalontai piti parempana, että oppilas voisi itse valita
tehtävät. Tällöin opettajan taholta ei tule
viestiä, että olet heikko. Mahdollisuus valita tehtävät tukee
myös oppilaan itsetuntoa. Eriyttävässä käytännössä
nopeille annetaan enemmän tehtäviä.
Szalontai kertoi, että unkarilaisessa
koulujärjestelmässä 12-vuotiaiden tasoerot
matematiikassa alkavat kasvaa. Unkarissa kaksi kolmasosaa jatkaa
matematiikan opiskelua 18 ikävuoden jälkeenkin. Esimerkiksi
Englannissa matematiikan opiskelu on mahdollista lopettaa jo 16-vuotiaana.
Tehokas oppitunti
Tibor Szalontain mukaan opettamisessa interaktiivisuus on tärkeää.
Opetuksessa käytetään ongelmanratkaisutehtäviä,
joita voidaan ratkoa yksin, pienryhmissä tai yhdessä koko luokan kanssa.
Viimeinen on vallitseva ja suositeltavin tapa.
Tibor Szalontai esitti kymmenen kohtaa, joiden mukaan
tehokas oppitunti etenee.
- Kysymyksen asettaminen ja tehtävän anto, jonka tulisi olla lyhyt
ja selkeä. Opettajan on
varmistettava, että kaikki ymmärtävät, mitä
halutaan.
- Luokassa kiertely, oppilaat työskentelevät itsenäisesti ja opettaja
seuraa työskentelyä. Itsenäinen työ kehittää kirjallisia kykyjä ja lisää
ongelmanratkaisutaitoja.
- Itsenäisen työskentelyn lopettaminen.
- Yhteiskeskustelu alkaa. Opettaja kehottaa joitain oppilaita selvittämään,
miten he ratkaisivat tehtävän. Yhteiskeskustelu kehittää käsitteellistä
ajattelua ja kommunikointia. Muiden ideat opitaan hyväksymään ja omat
mielipiteet perustelemaan.
Kuka on samaa mieltä, eri mieltä?
- Kerätään ideat ja niiden perustelut.
Miksi, miten? Opettaja ei vielä sano, mitkä ovat oikein tai väärin.
- Opettaja lopettaa keskustelun ja kertoo mitkä vastaukset ovat oikein tai
väärin ja miksi.
- Palaute. Kuka osasi ratkaista oikein? (Tämä on parempi kysymys kuin
"osasivatko kaikki ratkaista?", johon ei saada selkeää vastausta.)
- Virheellisten tai puutteellisten vastausten korjaaminen koulun alaluokilta
lähtien, oppilaat itse etsivät virheensä ja korjaavat ne.
Yksityiskohtaiseen
korjaamiseen ei kuitenkaan tunnilla ole aikaa, vaan se voidaan antaa
ylimääräiseksi kotitehtäväksi.
- Arvioiminen. Oppilaille annetaan tunnustusta hyvistä suorituksista
ja ideoista sekä kannustusta.
- Lopuksi opettaja voi esimerkiksi muuttaa vähän ongelmaa. Voidaan
tarkastella erilaisia ratkaisuja, antaa historiallista taustaa ja
kirjallisuusviitteitä. Ongelmaa voidaan yleistää ja etsiä analogisia
ongelmia. Voidaan myös palata ongelmaan ja keskustella siitä, mistä
ratkaisuidea tuli. Miten ajattelimme tehtävää ratkaistessamme?
Tehokkaalla oppitunnilla ei haaskata
minuuttiakaan, keskitytään vain matematiikkaan ja luokka yritetään pitää
yhteistyössä. Yhteiskeskustelu auttaa heikkoja oppilaita. Noin
12-vuotiaaksi saakka selvitään eriyttämisellä (enemmän tehtäviä siihen
pystyville, eritasoisia kotitehtäviä, esim. 3 eri tasoa, josta oppilaat
saavat itse valita).
Luokan yhteisen toiminnan tavoitteet ja mahdollisuudet:
- kehittää kommunikaatiotaitoja
- kehittää taitoa argumentoida ja päästä
yhteisymmärrykseen
- rakentaa matemaattisen tiedon struktuureja
-
hyödyntää yksittäisen oppilaan virheitä ja väärinkäsityksiä koko
luokan oppimisen tukemiseksi
Oppilaiden yksilöllisen työskentelyn tavoitteet ja mahdollisuudet:
- tutkiminen, ratkaisuideoiden hakeminen, suunnittelu ja kokeilu
- harjoittelu,
suoritus ja itsekriittinen kehittyminen
- onnistumisen tunne, "heureka"-elämykset
- mallien ja apuvälineiden käyttö: palikat, kuvat, taulukot jne.
- opettaja toimii valmentajana, kannustaa oppilaita ja edellyttää
jatkuvalla harjoittelulla parempia tuloksia.
Oppitunnin voi aloittaa opettajan johtamalla n. 10 minuutin
päässälaskuharjoituksella, jossa käsitellään kertolaskua, jakolaskua, lukujonoja tms.
Tunnin aikana oppilaille annetaan 5-8 tehtävää, esim. neljä yhtälöä ja neljä
sanallista tehtävää. Tehtävät tulee antaa yksi kerrallaan ja kunkin tehtävän
yhteydessä käydä keskustelua ja antaa palautetta. Näin edellisessä
tehtävässä opittu tukee seuraavan tehtävän suoritusta. Jos oppilaat saavat
kaikki tehtävät kerrallaan on mahdollista, että erityisesti heikoimmat
oppilaat eivät jaksa keskittyä riittävän pitkään (20...30 minuuttia). Antamalla
tehtävät yksi kerrallaan opettaja pystyy myös paremmin pitämään luokkaa
koossa ja hallinnassa. Oppilaat saavat tunteen, että
opettaja on kiinnostunut heistä yksilöinä.
Esimerkki uuden asian käsittelystä, yhtälön ratkaiseminen:
- Yhtälö esim. 2(x - 2) - 3(2x + 9) = 9 tai
(2x - 3)/2 + 1
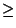 2
2
- Mikä on ensimmäinen
askel yhtälön ratkaisemiseksi? Ei siis vielä pyydetä ratkaisua, vain
ensimmäistä toimenpidettä.
- Keskustelua voidaan käydä opettajan johdolla
tai oppilaiden välillä ryhmissä. Myös yksilöllinen työskentely on
mahdollista.
- Ensimmäisen askeleen jälkeen yhtälön muoto on jo tuttu:
2x - 4 - 6x -27 = 9 tai 2x - 3 + 2 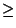 4
4
- Oppilaiden mahdolliset virheet oikaistaan ja keskustellaan niistä
rakentavasti.
- Vuorovaikutuksessa luokan kanssa opettajan tulee pyrkiä
interaktiiviseen kyselytekniikkaan. Kukin kysymys koskettaa vain rajoitettua
aihetta. Kysymykset asetetaan niin, että parhaiden lisäksi mahdollisimmman moni
oppilas voisi vastata niihin. Opettaja kysyy myös muilta oppilailta,
yhtyvätkö he vastaukseen.
Oppimisteorioita
- Assosiatiivinen oppiminen / opettaminen (Comenius)
- askel askeleelta vaikeampaa
- konkreetisesta abstraktiin
- läheltä kaus
- helposta vaikeaan
- visuaalisesta abstraktiin
- kokeellisesti eteneminen
(Nämä kohdat sopivat kaikkeen opetukseen.)
- Ärsyke - reaktio
- ohjelmoitu opettaminen
- pienet askeleet
- palautteen antaminen välittömästi
- Apuvälineitä käyttävä opetus (Piaget, Inhelder)
- Ensin lapset oppivat apuvälineiden (esim. loogiset palat, värisauvat)
avulla. Tämän jälkeen apuvälineitä ei käytetä,
mutta ne ovat kuitenkin ajatuksissa tehtäviä
tehdessä. Viimeisessä vaiheessa ei tarvita edes visuaalista
mielikuvaa apuvälineistä.
Erilaisia lähestymistapoja matematiikan opetukseen
- Jotkut opettajat seuraavat historiallista matematiikan kehitystä.
Tällöin esim. luku 0 opitaan luonnollisten lukujen 1,2,... jälkeen.
- Opettaja yrittää tehdä käsitteet ymmärrettäviksi oppilaiden ikäryhmälle
yksinkertaistamalla asiaa.
- Strukturaalis-formaalinen lähestymistapa. Uudessa matematiikassa haluttiin
opettaa abstraktia algebraa jo varhaisessa vaiheessa.
- Ongelmalähtöinen lähestymistapa (Pólya, Freudenthal). Oppilaalle
yritetään saada "heureka"-kokemus mahdollisimman usein. Käytetään
"ohjattua uudelleen keksimistä", ei jätetä asian selviämistä sattuman
varaan.
- Yksilökeskeinen opetustapa; kukin työskentelee omien
töidensä parissa eikä opetuksessa ole selkeää järjestelmää.
- Tietokonesuuntautunut lähestymistapa.
- Sovellussuuntautunut lähestymistapa. Käytetään projekteja
ja pienryhmätyöskentelyä.
Unkarilaisessa opetuksessa käytetään kaikkia lähestymistapoja.
Jokainen lähestymistapa on tärkeä ja hyvä
yhdistettynä muihin, ei ainoana lähestymistapana.
Ks. myös Szalontai-Näätänen:
Joitakin ajatuksia
matematiikan opetuksesta (Solmu 3/2002)
Huomioita unkarilaista matematiikan oppikirjoista:
- Kirjoissa on runsaasti eri tyyppisiä tehtäviä, myös kirjallisia sekä
kuviin tai taulukoihin liittyviä.
- Tehtäviin on usein liitetty havainnollistava piirros tai kuva.
- Pelkkiä numerolaskuja on vähän, niiden sijasta on paljon ongelmanratkaisu- ja
päättelytehtäviä.
- Jo 4. vuoden sisällöt ovat huomattavasti vaativampia ja käsittelevät laajemmin
eri matematiikan aloja kuin meillä.
- Geometriassa käsitellään pinta-alat, tilavuudet, koordinaatisto ja kulmat.
- Tehtävien tärkeimmät ominaisuudet ovat monipuolisuus ja mahdollisuus erilaisiin variaatioihin.
- Esimerkki hauskasta tehtävästä on numeroristikko (kuin sanaristikko
mutta numeroin).
Seuraavissa luvuissa käsitellään tarkemmin eri aiheiden opettamista.
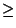 2
2
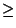 4
4

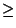 2
2
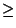 4
4