Usein helpoista asioista tehdään tarpeettoman vaikeita. Laskutoimitusten ominaisuuksien oppiminen voidaan aloittaa keskustelulla erilaisista (tavallisesta poikkeavista) laskutoimituksista ja selvittää, mitkä laskusäännöt milloinkin ovat voimassa:
Matriisilaskennan ja lineaarialgebran perusteet antavat mahdollisuuksia mielekkäisiin virikkeisiin jopa 16-vuotiaille oppilaille.
Algebraan tutustuminen aloitetaan mittauksilla ja yksiköillä sekä kysymyksillä, jotka liittyvät oppilaaseen itseensä.
Tärkeä ongelma on myös, miten voidaan saada suuret luvut ymmärrettävämpään muotoon.
Esim. Olisiko Suomessa tarpeeksi tilaa kutsua kaikki maailman ihmiset
Suomeen? Oletetaan, että jokainen ihminen vaatii tilaa yhden
neliömetrin ja ihmisiä on maailmassa
6 
109.
Tilaa tarvitaan siis 6 109
1 m2 = 6 000 km2.
Koska Suomen pinta-ala on noin 337 000 km2, voitaisiin kaikki maailman ihmiset kutsua Suomeen.
Harjoitustehtävä
Neliön muotoinen alue (kuva alla), jonka kulmissa kasvaa puu, halutaan kaksinkertaistaa. Kulmissa olevia puita ei kuitenkaan saa kaataa. Onko tehtävälle ratkaisua?
Oppilaiden mielenkiito saadaan paremmin pysymään aiheessa, jos ratkaisuun käytettävää aikaa ei ole liikaa. Hetken kuluttua tehtävänannosta käydään ratkaisusta keskustelu. Näin nekin, jotka eivät ole osanneet ratkaista tehtävää saavat idean ja osaavat ehkä ratkaista seuraavan tehtävän.
Kymmenvuotiaille aletaan opettaa kolmioiden ja nelikulmioiden määritelmiä, vaikka sana määritelmä ei ole selkeä. Pitäisi siis painottaa sanojen tarkoitusta. Esim. Tämä on määritelmä ja nämä ovat määritelmän seurauksia. Aksiooma-sanan voi ajatella tarkoittavan sitä, mikä nähdään. Ennen neljäätoista ikävuotta teorioita ei juuri esitetä. Joskus oppilaita ohjattaessa voidaan löytää jokin matemaattinen ominaisuus. Sen jälkeen voidaan yhdessä pohtia kysymystä "jos tämä on tosi tässä yhteydessä, niin onko se tosi muuallakin?"
Esim. Kolmion mediaanit, eli keskijanat leikkaavat samassa pisteessä, joka jakaa keskijanat niin, että sivun puoleinen osa on kolmasosa koko keskijanasta. Leikkauspistettä sanotaan kolmion painopisteeksi. Tässä päämäärää ei kerrota oppilaalle, vaan annetaan ohjeita, joiden avulla pyritään tuomaan esille edelliset ominaisuudet.
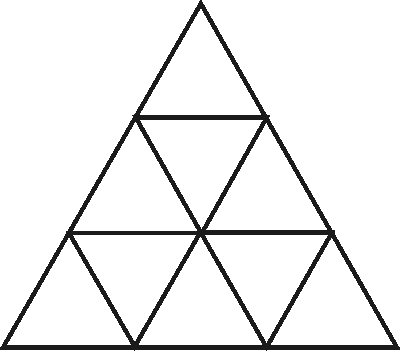
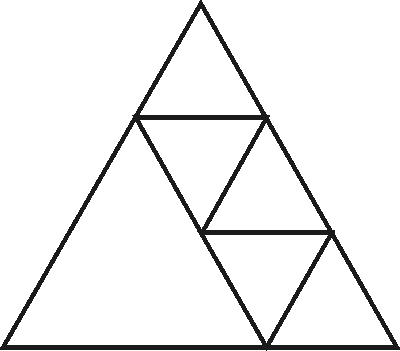
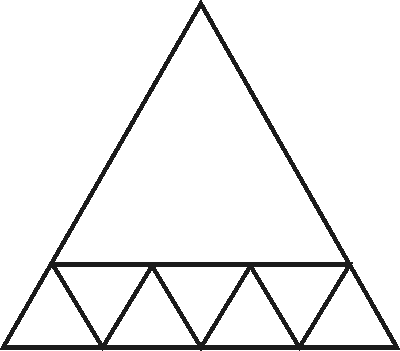
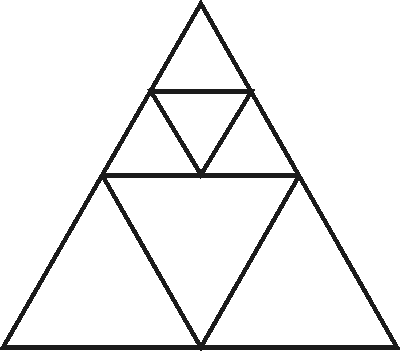
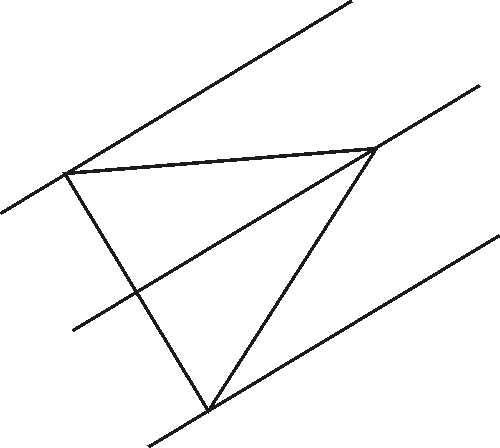
Esim. Voidaanko mikä tahansa kolmio jakaa neljään (kuuteen, seitsemään, kahdeksaan, yhdeksään, n:ään, n vähintään 6:teen) yhdenmuotoiseen kolmioon? Seuraavissa kuvissa esitetään ratkaisu tasasivuisen kolmion tapauksessa.
 |
 |
 |
 |
 |
Tehtävä: Konstruoi tasasivuinen kolmio, jonka kärjet ovat kolmella yhdensuuntaisella viivalla.
Ratkaisu:
Alkeelliseen yhtälönratkaisuun oppilaan tutustuvat jo ensimmäisellä luokalla. Muuttujan paikalla on tyhjää tai kirjain. Muuttuja voi tehdä lauseen myös epätodeksi. Oppilaat tutustuvat toden ja epätoden käsitteisiin.
Esim. 4 + 1 = 8 on epätosi
4 + 1 = 5 on tosi
Esim. 3 + ___ = 7
Kysytyn luvun paikka voidaan jättää tyhjäksi, korvata tyhjä tila neliöllä, pisteillä, millä vain. Halutaan korostaa puuttuvan numeron paikkaa, eli tuntematonta, joka tekee laskun todeksi.
Konkreettisista laskuista edetään abstrakstimpiin laskuihin.
Esim. Tee laskutoimitukset
Oppilaita rohkaistaan tuottamaan myös kirjoitettuja vastauksia.
Aluksi tehtäviä ratkaistaan kokeilemalla, muuta ei vaadita.
Esim. Mikä numero voidaan kirjoittaa a:n paikalle?
a + 3,4 = 5,6
a = ____
Esim. Jaa 20,3 kg kolmeen osaan siten, että kevyin on puolet keskimmäisestä ja keskimmäinen puolet painavimmasta.
Esim. Jaakko-setä tienasi 2400 euroa helmikuussa. Hän käytti viidesosan ruokaan, kuudesosan laskuihin ja neljänneksen puutarhaan. Paljonko hänellä jäi säästöön?
Verrannollisuuslaskuihin tutustutaan mm. tällaisin esimerkein.
Esim. Neljä metriä kangasta maksaa 16 euroa. Kuinka paljon maksaa 7 metriä kangasta?
Yksi metri maksaa 4 euroa, 7 metriä 28 euroa.
Taulukko auttaa hahmottamaan suoraan verrannollisuutta.
4 m maksaa 16 e
7 m maksaa 16 7/4 e
------------------------
1 m maksaa 16 e / 4 = 4 e
7 m maksaa 16 e / 4 7 = 28 e
n m maksaa 16 e / 4 n
= 4n e
Seuraava animaatioesitys auttaa ymmärtämään kääntäen verrannollisuuden idean:
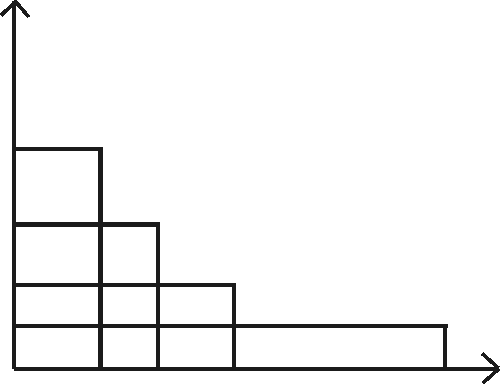
Kaikilla kuvan suorakulmioilla on sama pinta-ala. Kun toista sivua lyhennetään, on toista pidennettävä, jotta sama pinta-ala säilyisi.
Vaakametodiin lineaarisille yhtälöille tutustutaan 11-vuotiaina. Tähän asti on riittänyt, että vastaukset yhtälöihin keksitään kokeilemalla. Oikean vaa'an käyttö esimerkkinä havainnollistaa tilannetta. Kun toisesta vaakakupista otetaan jotain pois, on sama otettava toisestakin, jotta tasapaino säilyy. Myöhemmin vaaka havainnollistetaan piirroksena.
Miten lasketaan helposti, että
1234321234321 2468642468641
- 1234321234320 = 1234321234320
2468642468641 + 1234321234321?
Merkitään 1234321234321 = a
Väite on a(2a - 1) - (a - 1) = (a - 1) (2a - 1) + a
Vasen puoli on 2a2 - a - a + 1 = 2a3 - 3a + 1 +a, todetaan, että se on sama kuin oikea puoli.
Piagét'n tutkimustulosten perusteella oppilaiden valmius erilaisiin matemaattisiin ongelmiin vaihtelee paljon, esimerkiksi toiset voivat hallita tiettyjä asioita jo kymmenenvuotiaina, kun taas toiset ymmärtävät asian vasta neljätoistavuotiaina.
Kahdestatoista ikävuodesta eteenpäin voidaan laskea seuraavanlaisia laskuja:
Sievennä
X2 + Y2 – 5X2 + X2/2 + Y2/2 =
Täydennä
X/2 + Y/2 + ___ X - ___Y = - 1/2X – 1/3Y
