

Matti Lehtinen
Esitetään Solmun 1/2002 tehtävien 16-30 ratkaisut; tehtävien 1-15 ratkaisut esitettiin edellisessä numerossa 2/2002.
16. Määritä kymmenjärjestelmässä kirjoitetun luvun ![]() numeroiden
summan numeroiden summan numeroiden summa.
numeroiden
summan numeroiden summan numeroiden summa.
Ratkaisu.
Olkoon ![]() luvun
luvun ![]() numeroiden summa ja olkoon
numeroiden summa ja olkoon
![]() . Koska
. Koska
![]() ,
luvussa
,
luvussa ![]() on enintään 8004 numeroa. Siis
on enintään 8004 numeroa. Siis
![]() . Näin ollen
. Näin ollen
![]() ja
ja
![]() . Mutta
. Mutta
![]() . Koska
. Koska
![]() ,
,
![]() . Silloin myös
. Silloin myös
![]() . Ainoa mahdollisuus on, että
. Ainoa mahdollisuus on, että
![]() .
.
17. Olkoon ![]() kaikkien sellaisten funktioiden lukumäärä, jotka on
määritelty joukossa
kaikkien sellaisten funktioiden lukumäärä, jotka on
määritelty joukossa
![]() ,
, ![]() positiivinen kokonaisluku,
ja joiden arvot kuuluvat joukkoon
positiivinen kokonaisluku,
ja joiden arvot kuuluvat joukkoon
![]() ja olkoon
ja olkoon ![]() kaikkien sellaisten funktioiden lukumäärä, jotka on määritelty joukossa
kaikkien sellaisten funktioiden lukumäärä, jotka on määritelty joukossa
![]() ,
, ![]() positiivinen kokonaisluku, ja joiden arvot
kuuluvat joukkoon
positiivinen kokonaisluku, ja joiden arvot
kuuluvat joukkoon
![]() . Määritä
. Määritä ![]() :n pienin
mahdollinen arvo.
:n pienin
mahdollinen arvo.
Ratkaisu.
Tehtävän oletusten mukaan ![]() ja
ja ![]() .
Tarkastellaan ensin tapauksia
.
Tarkastellaan ensin tapauksia ![]() . Luku
. Luku ![]() päättyy
ykköseen. Jos olisi
päättyy
ykköseen. Jos olisi ![]() , olisi
, olisi
![]() . Koska luku
. Koska luku ![]() päättyy seitsemään, se ei voi
olla tekijänä luvussa
päättyy seitsemään, se ei voi
olla tekijänä luvussa ![]() . Siis
. Siis
![]() . Mutta
yhtälöllä
. Mutta
yhtälöllä ![]() on ratkaisu
on ratkaisu ![]() ,
, ![]() . Tarkastellaan
tapauksia
. Tarkastellaan
tapauksia ![]() . Luku
. Luku ![]() päättyy yhdeksään. Mutta
jaollisuus estää, että olisi
päättyy yhdeksään. Mutta
jaollisuus estää, että olisi ![]() . Siis
. Siis ![]() :n
minimiarvo on 11.
:n
minimiarvo on 11.
18. Olkoot ![]() ,
, ![]() , ...,
, ..., ![]() ei-positiivisia
lukuja. Todista, että
ei-positiivisia
lukuja. Todista, että
Ratkaisu.
Osoitetaan induktiolla, että
![]() Väite pätee, kun
Väite pätee, kun ![]() :
koska
:
koska
![]() , niin
, niin
![]() . Oletetaan, että (1) on tosi. Silloin samasta
syystä kuin edellä
. Oletetaan, että (1) on tosi. Silloin samasta
syystä kuin edellä
![]()
19. Neliön ![]() sivun pituus on 1. Olkoon
sivun pituus on 1. Olkoon ![]() mielivaltainen sivun
mielivaltainen sivun ![]() ja
ja ![]() mielivaltainen sivun
mielivaltainen sivun ![]() piste ja olkoot
piste ja olkoot ![]()
![]() :n ja
:n ja ![]() :n
leikkauspiste ja
:n
leikkauspiste ja ![]()
![]() :n ja
:n ja ![]() :n leikkauspiste. Määritä ne pisteet
:n leikkauspiste. Määritä ne pisteet ![]() ja
ja ![]() , joille nelikulmion
, joille nelikulmion ![]() ala on suurin mahdollinen.
ala on suurin mahdollinen.
Ratkaisu.
Kolmiot ![]() ja
ja ![]() ovat yhdenmuotoiset.Oletetaan, että
ovat yhdenmuotoiset.Oletetaan, että
![]() . Silloin
. Silloin ![]() , ja yhtäsuuruus pätee vain, kun
, ja yhtäsuuruus pätee vain, kun
![]() . Olkoon
. Olkoon ![]() se janan
se janan ![]() piste, jolle
piste, jolle ![]() . Silloin
. Silloin
![]() ,
, ![]() ja
ja
![]() (yhtäsuuruus
vain, kun
(yhtäsuuruus
vain, kun ![]() ). Lisäksi
). Lisäksi
![]() . Siis
. Siis
![]() . Samankokoiset kolmiot
. Samankokoiset kolmiot
![]() ja
ja ![]() peittävät alle puolet puolisuunnikkaasta
peittävät alle puolet puolisuunnikkaasta ![]() ,
joten
,
joten
![]() . Samoin
osoitetaan, että
. Samoin
osoitetaan, että
![]() . Siis
. Siis
![]() . Yhtäsuuruus pätee
edellisten tarkastelujen mukaan silloin ja vain silloin, kun
. Yhtäsuuruus pätee
edellisten tarkastelujen mukaan silloin ja vain silloin, kun
![]() .
.
20. Suunnikkaan ![]() sivun
sivun ![]() keskipiste on
keskipiste on ![]() ja
ja ![]() on pisteen
on pisteen ![]() kohtisuora projektio suoralla
kohtisuora projektio suoralla ![]() . Osoita, että
. Osoita, että ![]() on tasakylkinen
kolmio.
on tasakylkinen
kolmio.
Ratkaisu.
Leikatkoon ![]() suoran
suoran ![]() pisteessä
pisteessä ![]() . Koska
. Koska ![]() ,
kolmiot
,
kolmiot ![]() ja
ja ![]() ovat yhteneviä. Siis
ovat yhteneviä. Siis ![]() . Koska
. Koska
![]() on suorakulmainen kolmio, sen ympäri piirretyn ympyrän
halkaisija on hypotenuusa
on suorakulmainen kolmio, sen ympäri piirretyn ympyrän
halkaisija on hypotenuusa ![]() ja ympyrän keskipiste
ja ympyrän keskipiste ![]() :n
keskipiste
:n
keskipiste ![]() . Siis
. Siis ![]() , ja
, ja ![]() on tasakylkinen.
on tasakylkinen.
21. Pisteet ![]() ,
, ![]() ,
, ![]() ja
ja ![]() ovat pallon pinnan eri
pisteitä. Janat
ovat pallon pinnan eri
pisteitä. Janat ![]() ja
ja ![]() leikkaavat toisensa pisteessä
leikkaavat toisensa pisteessä ![]() .
Pisteet
.
Pisteet ![]() ,
, ![]() ja
ja ![]() ovat
yhtä etäällä pisteestä
ovat
yhtä etäällä pisteestä ![]() . Osoita, että suorat
. Osoita, että suorat ![]() ja
ja ![]() ovat
kohtisuorassa toisiaan vastaan.
ovat
kohtisuorassa toisiaan vastaan.
Ratkaisu.
Pisteet ![]() ,
, ![]() ,
, ![]() ja
ja ![]() ovat samalla ympyrällä
ovat samalla ympyrällä
![]() ja samassa tasossa
ja samassa tasossa ![]() . Olkoon
. Olkoon ![]() pisteen
pisteen ![]() projektio tasolla
projektio tasolla ![]() . Suorakulmaiset kolmiot
. Suorakulmaiset kolmiot ![]() ,
, ![]() ja
ja
![]() ovat yhteneviä, joten
ovat yhteneviä, joten ![]() on kolmion
on kolmion ![]() ympäri
piirretyn ympyrän
ympäri
piirretyn ympyrän ![]() keskipiste. Leikatkoon suora
keskipiste. Leikatkoon suora ![]()
![]() :n myös pisteessä
:n myös pisteessä ![]() ja suoran
ja suoran ![]() pisteessä
pisteessä ![]() .
Ympyröiden
.
Ympyröiden ![]() ja
ja ![]() kehäkulmista saadaan
kehäkulmista saadaan
![]() . Kolmiot
. Kolmiot ![]() ja
ja ![]() ovat
yhdenmuotoiset. Koska
ovat
yhdenmuotoiset. Koska ![]() on
on ![]() :n halkaisija,
:n halkaisija,
![]() . Koska
. Koska ![]() ja siis
ja siis ![]() ,
niin tason
,
niin tason ![]() kaksi suoraa on kohtisuorassa
kaksi suoraa on kohtisuorassa ![]() :tä vastaan.
Täten
:tä vastaan.
Täten ![]() on kohtisuorassa tasoa
on kohtisuorassa tasoa ![]() vastaan ja erityisesti
vastaan ja erityisesti
![]() .
.
22. Teräväkulmaisen kolmion ![]() ympäri piirretty ympyrä
on
ympäri piirretty ympyrä
on ![]() . Olkoon
. Olkoon ![]() piste
piste ![]() :n sisäpuolella. Olkoot
:n sisäpuolella. Olkoot ![]() ,
,
![]() ja
ja ![]() ne pisteet,
joissa suorat
ne pisteet,
joissa suorat ![]() ,
, ![]() ja
ja ![]() myös leikkaavat
myös leikkaavat ![]() :n. Määritä ne
pisteet
:n. Määritä ne
pisteet ![]() , joille
, joille ![]() on tasasivuinen kolmio.
on tasasivuinen kolmio.
Ratkaisu.
Piste ![]() ei voi olla kolmion
ei voi olla kolmion ![]() ulkopuolella. Jos
ulkopuolella. Jos ![]() olisi esim. lyhyemmän kaaren
olisi esim. lyhyemmän kaaren ![]() määrittämässä segmentissä,
olisi se kaarista
määrittämässä segmentissä,
olisi se kaarista ![]() , joka ei sisällä pistettä
, joka ei sisällä pistettä ![]() , suurempi
kuin
, suurempi
kuin ![]() . Olkoon siis
. Olkoon siis ![]() sellainen
sellainen ![]() :n sisäpiste, että
kolmio
:n sisäpiste, että
kolmio ![]() on tasasivuinen. Kolmiosta
on tasasivuinen. Kolmiosta ![]() saadaan
saadaan
![]() . Samoin saadaan
. Samoin saadaan
![]() ja
ja
![]() . Mutta tunnetusti niiden pisteiden
joukko, joista annettu jana näkyy annetussa kulmassa koostuu
kahdesta ympyränkaaresta janan eri puolilla. Kolmion
. Mutta tunnetusti niiden pisteiden
joukko, joista annettu jana näkyy annetussa kulmassa koostuu
kahdesta ympyränkaaresta janan eri puolilla. Kolmion ![]() sisällä on siten enintään yksi tehtävän ehdon toteuttava piste
sisällä on siten enintään yksi tehtävän ehdon toteuttava piste
![]() . Tällainen piste myös on olemassa, koska edellä saatu
kulmaehto merkitsee, että mainitut kaaret ovat kokonaan kolmion
sisällä ja siis leikkaavat toisensa.
. Tällainen piste myös on olemassa, koska edellä saatu
kulmaehto merkitsee, että mainitut kaaret ovat kokonaan kolmion
sisällä ja siis leikkaavat toisensa.
23. ![]() kiveä asetetaan yhdeksi tai useammaksi kasaksi.
Mikä on eri
kasoissa olevien kivien lukumäärien tulon suurin mahdollinen arvo?
kiveä asetetaan yhdeksi tai useammaksi kasaksi.
Mikä on eri
kasoissa olevien kivien lukumäärien tulon suurin mahdollinen arvo?
Ratkaisu.
Olkoot ![]() ,
, ![]() ,
, ![]() ,
, ![]() positiivisia
kokonaislukuja, joiden summa on
positiivisia
kokonaislukuja, joiden summa on ![]() . Tehtävä on maksimoida tulo
. Tehtävä on maksimoida tulo
![]() . Eri vaihtoehdot läpikäymällä havaitaan, että
jos
. Eri vaihtoehdot läpikäymällä havaitaan, että
jos ![]() , maksimi on
, maksimi on ![]() ja se saadaan, kun
ja se saadaan, kun ![]() .
Olkoon
.
Olkoon ![]() . Maksimitapauksessa ei voi olla
. Maksimitapauksessa ei voi olla ![]() , koska
tulo suurenisi, jos jokin
, koska
tulo suurenisi, jos jokin ![]() korvattaisiin
korvattaisiin ![]() :llä ja
:llä ja
![]() jäisi pois. Myöskään mikään
jäisi pois. Myöskään mikään ![]() ei ole
ei ole ![]() , koska jos
, koska jos
![]() , niin
, niin ![]() ; tulo suurenisi, jos
; tulo suurenisi, jos ![]() korvattaisiin luvuilla
korvattaisiin luvuilla ![]() ja
ja ![]() . Minkään
. Minkään ![]() :n ei
tarvitse olla 4, sillä
:n ei
tarvitse olla 4, sillä ![]() , tulo ei muutu, jos
, tulo ei muutu, jos ![]() korvataan kahdella 2:lla. Lisäksi
korvataan kahdella 2:lla. Lisäksi ![]() enintään kahdella
enintään kahdella
![]() :n arvolla, koska
:n arvolla, koska ![]() , mutta
, mutta
![]() . Maksimitilanteessa on siis vain lukuja
. Maksimitilanteessa on siis vain lukuja ![]() ja
ja ![]() ;
jälkimmäisiä enintään kaksi kappaletta. Maksimitulot ovat siten
seuraavat: jos
;
jälkimmäisiä enintään kaksi kappaletta. Maksimitulot ovat siten
seuraavat: jos ![]() , maksimi on
, maksimi on ![]() , jos
, jos ![]() , maksimi
on
, maksimi
on
![]() , jos
, jos ![]() , maksimi on
, maksimi on ![]() . Jos
. Jos
![]() , maksimi on 1.
, maksimi on 1.
24. Määritellään lukujonot ![]() ja
ja ![]() seuraavasti:
seuraavasti:
![]() ,
, ![]() ,
,
![]() ,
,
![]() , kun
, kun
![]() , 2, ... Määritä
pienin
, 2, ... Määritä
pienin ![]() , jolle
, jolle ![]() .
.
Ratkaisu.
Jos ![]() , niin
, niin
![]() . Osoitetaan
induktiolla, että
. Osoitetaan
induktiolla, että
![]() kaikilla
kaikilla ![]() . Väite
pätee, kun
. Väite
pätee, kun ![]() :
:
![]() . Oletetaan, että
. Oletetaan, että
![]() . Silloin
. Silloin
![]() , joten
, joten ![]() . Näin ollen
. Näin ollen
![]() ja
ja
![]() . Tästä seuraa,
että
. Tästä seuraa,
että
![]() , joten tehtävän vastaus on
, joten tehtävän vastaus on
![]() .
.
25. Tasossa on annettuina 2000 pistettä. Osoita, että pisteet voidaan yhdistää pareittain 1000 janalla, jotka eivät leikkaa toisiaan.
Ratkaisu.
Jos pisteet yhdistetään pareittain 1000 janalla niin, että
janojen pituuksien summa on mahdollisimman pieni, niin janat
eivät leikkaa toisiaan. Jos nimittäin ![]() ja
ja ![]() leikkaisivat
pisteessä
leikkaisivat
pisteessä ![]() , olisi
, olisi
![]() .
.
26. Eräs tehdas tuottaa samankokoisia säännöllisiä
tetraedreja. Tehdas
maalaa tetraedrinsa neljällä värillä ![]() ,
, ![]() ,
, ![]() ja
ja ![]() , kukin
tahko omallaan. Montako erilaista tetraedria on mahdollista tuottaa?
, kukin
tahko omallaan. Montako erilaista tetraedria on mahdollista tuottaa?
Ratkaisu.
Olkoot värit
![]() . Väritetty tetraedri
voidaan aina kääntää niin, että pohjan väri on
. Väritetty tetraedri
voidaan aina kääntää niin, että pohjan väri on ![]() ja että
ja että
![]() -väri osoittaa esim. etelään. Silloin on vain kaksi
mahdollisuutta sijoittaa
-väri osoittaa esim. etelään. Silloin on vain kaksi
mahdollisuutta sijoittaa ![]() - ja
- ja ![]() -värit:
-värit: ![]() luoteeseen ja
luoteeseen ja
![]() koilliseen tai päinvastoin. Erilaisia tetraedrivärityksiä on
siis vain kaksi.
koilliseen tai päinvastoin. Erilaisia tetraedrivärityksiä on
siis vain kaksi.
27. Maalaiskoulussa on 20 lasta. Jokaisella kahdella lapsella on yhteinen isoisä. Todista, että eräällä isoisällä on ainakin 14 lastenlasta.
Ratkaisu.
Olkoot ![]() ja
ja ![]()
![]() :n isoisät. Olkoon lapsista kaikkiaan
:n isoisät. Olkoon lapsista kaikkiaan
![]() kappaletta,
kappaletta, ![]() , sellaisia, joiden isoisät ovat
, sellaisia, joiden isoisät ovat ![]() ja
ja
![]() . Olkoon
. Olkoon ![]() lapsi, jonka isoisät eivät ole
lapsi, jonka isoisät eivät ole ![]() ja
ja ![]() .
Kuitenkin toinen näistä on
.
Kuitenkin toinen näistä on ![]() :n isoisä; olkoon toinen isoisä
:n isoisä; olkoon toinen isoisä
![]() ja toinen
ja toinen ![]() . Lapsen
. Lapsen ![]() toinen isoisä on joko
toinen isoisä on joko ![]() tai
tai ![]() ja toinen isoisä joko
ja toinen isoisä joko ![]() tai
tai ![]() . Isoisiä on siis enintään 3,
ja
. Isoisiä on siis enintään 3,
ja ![]() on kaikkien niiden
on kaikkien niiden ![]() :n lapsen isoisä, joiden isoisät
eivät ole
:n lapsen isoisä, joiden isoisät
eivät ole ![]() ja
ja ![]() . Olkoon
. Olkoon ![]() :lla ja
:lla ja ![]() :llä
:llä ![]() yhteistä
lapsenlasta; silloin
yhteistä
lapsenlasta; silloin ![]() :llä ja
:llä ja ![]() :llä on
:llä on ![]() yhteistä
lapsenlasta. Ainakin yksi luvuista
yhteistä
lapsenlasta. Ainakin yksi luvuista ![]() ,
, ![]() ,
, ![]() on
enintään 6. Jos esim.
on
enintään 6. Jos esim. ![]() , niin
, niin ![]() :llä on
:llä on
![]() lapsenlasta.
lapsenlasta.
28. Toisessa koulussa oli 13 tyttöä ja 10 poikaa. Opettaja jakoi namusia. Kaikki tytöt saivat keskenään yhtä monta ja kaikki pojat keskenään yhtä monta. Kukaan ei jäänyt ilman. Osoittautui, että tapa, jolla opettaja jakoi namuset, oli ainoa tapa, joka täytti edellä kuvatut ehdot. Montako namusta opettajalla enintään oli?
Ratkaisu.
Jos namuja oli ![]() ja jos jokainen poika sai
ja jos jokainen poika sai ![]() ja
jokainen tyttö
ja
jokainen tyttö ![]() namua, niin
namua, niin ![]() . Yhtälön
yksittäisratkaisu on
. Yhtälön
yksittäisratkaisu on ![]() ,
, ![]() ja yleinen ratkaisu
ja yleinen ratkaisu ![]() ,
, ![]() , missä
, missä ![]() on mielivaltainen kokonaisluku.
Koska
on mielivaltainen kokonaisluku.
Koska ![]() ja
ja ![]() , on oltava
, on oltava ![]() ja
ja ![]() eli
eli
![]() . Jos
. Jos
![]() ,
tehtävällä on enemmän kuin
yksi ratkaisu. Jos
,
tehtävällä on enemmän kuin
yksi ratkaisu. Jos ![]() , ehto sievenee muotoon
, ehto sievenee muotoon ![]() .
Tällöin ratkaisuja on vain yksi. Opettajalla oli enintään 260
namusta.
.
Tällöin ratkaisuja on vain yksi. Opettajalla oli enintään 260
namusta.
29. Todista, että
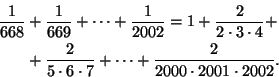
Ratkaisu.
Jaetaan
![]() osamurtoihin:
yhtälöstä
osamurtoihin:
yhtälöstä
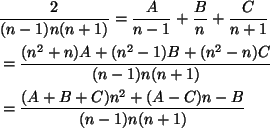
saadaan ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Siis
. Siis
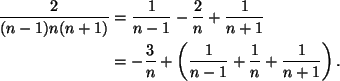
Mutta näin ollen
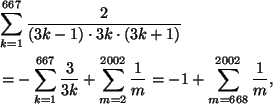
mikä on sama kuin tehtävän väitös.
30. Olkoon
![]() positiivisten kokonaislukujen joukko.
Määritä kaikki
funktiot
positiivisten kokonaislukujen joukko.
Määritä kaikki
funktiot
![]() , joille
, joille
![]() kaikilla
kaikilla ![]() ,
,
![]() ja joille yhtälöllä
ja joille yhtälöllä
![]() on ainakin yksi
ratkaisu
on ainakin yksi
ratkaisu
![]() .
.
Ratkaisu.
Olkoon ![]() , Silloin
, Silloin
![]() . Tästä
seuraa induktiolla, että
. Tästä
seuraa induktiolla, että ![]() . Yhtälö
. Yhtälö
![]() on siis sama kuin
on siis sama kuin
![]() . Jos
. Jos ![]() , yhtälön
ratkaisuja ovat kaikki
, yhtälön
ratkaisuja ovat kaikki
![]() . Jos
. Jos ![]() , yhtälö saa
muodon
, yhtälö saa
muodon ![]() . Ratkaisuja voi olla vain parillisilla
. Ratkaisuja voi olla vain parillisilla ![]() :n
arvoilla. Jos
:n
arvoilla. Jos ![]() , niin
, niin ![]() . Kun
. Kun ![]() , yhtälöllä
on ratkaisu
, yhtälöllä
on ratkaisu ![]() . Tehtävällä on siis kaksi ratkaisua:
. Tehtävällä on siis kaksi ratkaisua: ![]() kaikilla
kaikilla ![]() ja
ja ![]() kaikilla
kaikilla ![]() .
.