Todistaminen on asia, joka liittyy kiinteästi matematiikkaan. Usein todistuksen kohteena on jokin matemaattinen ongelma: olemme löytäneet sille ratkaisun, ja todistuksen tarkoituksena on perustella tämän ratkaisun pätevyys.
Matematiikassa voidaan myös todistaa asioita mahdottomiksi:
tällaisia ongelmia ei voida lainkaan ratkaista. Tunnetuimmat
esimerkit lienevät jo antiikin kreikkalaisia askarruttaneet
kysymykset ympyrän neliöimisestä1
ja kuution kahdentamisesta2
siten, että ratkaisussa käytetään vain harppia ja viivotinta.
Näiden ongelmien täsmällinen muotoilu edellyttää tietysti
sitä, että olemme huolellisesti määritelleet ne operaatiot,
joita harpilla ja viivottimella on luvallista suorittaa.
Todistus kyseisten operaatioiden mahdottomuudelle
palautuu kuitenkin geometriasta lukujen maailmaan; esimerkiksi
kuution kahdentamisen tapauksessa siihen, ettei lukua
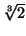koskaan saada tulokseksi sellaisesta laskusta, jossa
lähdetään liikkeelle kokonaisluvuista ja käytetään ainostaan
yhteen-, vähennys-, kerto- ja jakolaskua sekä neliöjuuren
ottamista.
Ammattimatemaatikko törmää aina silloin tällöin henkilöihin, jotka eivät näitä todistuksia sulata. Tällainen asenne saattaa olla elämässä hyödyllinen, mutta ainakin matematiikan kohdalla vain tiettyyn pisteeseen saakka. Myös yllä mainittujen ongelmien kohdalla yrittäjiä riittää vielä kauan sen jälkeen, kun niiden mahdottomuus on todistettu, ja useimmiten itse päättelyssä ei ole muuta vikaa kuin se, ettei rajoitusta harpin ja viivottimen käyttämisestä ole ymmärretty oikein.
Tähän liittyy havainto siitä, kuinka tärkeää matematiikassa on pitää kiinni täsmällisistä määritelmistä. Ainoana tieteenalana matematiikka antaa lopullisia vastauksia, mutta vain kysymyksiin, jotka on muotoiltu täsmällisesti. Jos määritelmien tarkkuudesta annetaan periksi, niin matemaattisista väitteistä tulee mielipidekysymyksiä.
Itse opin ymmärtämään hyvien määritelmien tärkeyden oikeastaan vasta väitöskirjaa tehdessäni. Siihen saattoi vaikuttaa myös työni ohjaajan antama neuvo siitä, kuinka tutkimustyön pitäisi edistyä: "Viikossa pitää todistaa yksi lause tai kaksi apulausetta, mutta hyvällä määritelmällä voi korvata lauseen."
Pekka Alestalo
1Ympyrän säde on annettu,
määritettävä sivun pituus sellaiselle neliölle, jolla on sama
pinta-ala kuin ympyrällä.
2Kuution sivun pituus on annettu,
määritettävä sivun pituus sellaiselle kuutiolle, jonka tilavuus
on kaksinkertainen alkuperäiseen verrattuna.