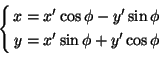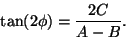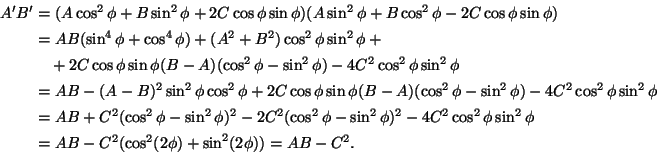PDF
Ellipsit, hyperbelit ja paraabelit vinossa
Matti Lehtinen
Opimme lukion analyyttisen geometrian kurssilla - ainakin, jos
kävimme lukiota vielä muutama vuosi sitten - että ellipsin, hyperbelin ja
paraabelin yhtälöt ovat
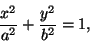 |
(1) |
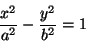 |
(2) |
ja
Yhtälöt
ovat yksinkertaisia ja kauniita. Käyrien monia ominaisuuksia voi melko
suoraan lukea yhtälöistä. Jos esimerkiksi a>b, niin ellipsin pisteille
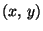 pätee
pätee
joten ellipsin lyhin etäisyys origosta on b ja pisin a, ja
nämä saavutetaan pisteissä
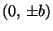 ja
ja
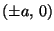 .
Tai koska
.
Tai koska
niin aina kun x ja y ovat itseisarvoltaan suuria hyperbelin
yhtälö (2) voi toteutua vain, jos jompikumpi tulon tekijä on lähes nolla.
Hyperbelin pisteet ovat siis suurilla |x|:n ja |y|:n arvoilla lähellä
suoria
Sanomme, että nämä suorat ovat hyperbelin asymptootit.
Yhtälöissä (1) - (3) on kuitenkin heikkous, johon muuan Solmun
lukija hiljattain kiinnitti huomionsa. Niissä oletetaan, että
käyrät on pantu poseeraamaan yksinkertaisen asentoon: ellipsin
keskipiste on origossa ja sen iso- ja pikkuakseli ovat
koordinaattiakseleilla, hyperbelillä on samantapainen origon ja
akselien suhteen symmetrinen asema ja paraabelin huippu on origossa ja
akselina on tasan y-akseli. Mutta eiväthän oikeat ellipsit
luonnossa ole näin. Satelliitin ellipsinmuotoisen radan iso- ja
pikkuakselit eivät asetu minkään itsestään selvän
maanpäällisen koordinaatiston mukaisesti.
"Yliopistomatematiikassa" ellipsien, hyperbelien ja paraabelien eli
yhdellä sanalla kartioleikkausten (nämä käyrät nimittäin
voi synnyttää ympyräkartion ja sen suhteen eri asennoissa
olevien tasojen leikkauksina, kuten jo antiikin ajoista on tiedetty)
tutkimuksessa sovelletaan nykyisin tavallisesti symmetristen
matriisien ominaisarvoteoriaa. Katsotaan tässä, mitä asiasta
saattaisi saada irti hiukan kotikutoisemmilla keinoilla, niin
sanotulla raa'alla laskemisella. Yritys saattaa vaikuttaa
masokistiselta, mutta sen tehtyään ymmärtää tason
geometriasta yhtä ja toista ja on saanut kohtuullisen hyvän
lausekkeiden manipulointiharjoituksen. Matematiikan tekemistä
helpottaa aina mukavasti se, että lausekkeiden käsittelyn
perusalgebra ei takkua!
Lähdetään liikkeelle ellipsistä tai hyperbelistä, jonka
yhtälö on
ja muistetaan, että vaihtoehtoisista etumerkeistä ylempi liittyy
ellipsiin, alempi hyperbeliin. Haluamme nyt asettaa kuvion muuhun kuin
alkuperäiseen asentoon. Sen sijaan, että kääntäisimme
kuviota, käännämmekin sen alla olevaa tasoa tai oikeastaan vain
koordinaattiakseleita. Sehän käy näin:
Jos P on piste ja A sen kohtisuora projektio
x-akselille ja B kohtisuora projektio y-akselille, niin P:n
koordinaatit x ja y ovat janojen OA ja OB pituudet, asianmukaisin
etumerkein varustettuina. Jos nyt koordinaattiakseleita kierretään vaikkapa
niin, että vanhan x-akselin ja uuden x'-akselin välinen kulma on 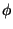 ,
niin pisteen P projektio uudella x'-akselilla on C ja uudella
y'-akselilla D. P aseman määrittävät nyt luvut x'=OC=DP ja
y'=OD=CP. Olkoot vielä E ja F pisteen C kohtisuorat projektiot
x-akselilla ja y-akselilla. Mutta
,
niin pisteen P projektio uudella x'-akselilla on C ja uudella
y'-akselilla D. P aseman määrittävät nyt luvut x'=OC=DP ja
y'=OD=CP. Olkoot vielä E ja F pisteen C kohtisuorat projektiot
x-akselilla ja y-akselilla. Mutta
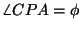 ,
joten
,
joten
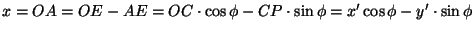 .
Vastaavasti
.
Vastaavasti
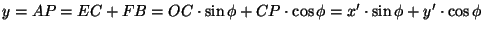 .
.
Piste 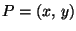 kuuluu ellipsiin tai hyperbeliin, jonka yhtälön
voimme kirjoittaa muotoon
kuuluu ellipsiin tai hyperbeliin, jonka yhtälön
voimme kirjoittaa muotoon
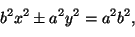 |
(4) |
silloin ja vain silloin, kun x ja y toteuttavat yhtälön (4).
Jos pisteen P sijainti ilmoitetaan uuden koordinaatiston avulla
luvuilla x', y', sen kuuluminen mainittuun käyrään riippuu
edelleen siitä, toteuttavatko x ja y yhtälön (4) vai ei.
Mutta tämä merkitsee, että käyrään kuulumisen ehto uusien
koordinaattien avulla lausuttuna täytyy olla
Kun tässä yhtälössä tehdään potenssiin korotukset ja
yhdistetään termit, saadaan
Käyrän yhtälö uusissa koordinaateissa on siis muotoa
Selvin muutos lähtöyhtälöön on "sekatermin" x'y'ilmaantuminen. A ja B eivät enää myöskään sisällä
sillä tavoin suoraa informaatiota käyrän muodosta kuin
yhtälöt (1) ja (2) tai (4).
Eräs mielenkiintoinen ominaisuus uudella muodolla on. Lasketaan
suure AB-C2. Se on
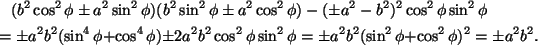
Kierron jälkeisessä yhtälössä suure on siis sama kuin
alkuperäisessä yhtälössä (4) (jossa C=0). Toisen asteen
yhtälön diskriminanttia muistuttava suure AB-C2 on invariantti
koordinaatistojen kierron suhteen. Erityisesti suureen AB-C2etumerkki paljastaa heti, onko yhtälöön (5) päädytty
soveltamalla kierron koordinaattimuutosta ellipsin vai hyperbelin
yhtälöön.
Jos haluamme ellipsimme tai hyperbelimme ei ainoastaan tiettyyn
asentoon vaan myös tiettyyn paikkaan, on tehtävä vielä origon
siirto, sanokaamme pisteeseen
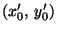 .
Se merkitsee vielä
uusia koordinaatteja
x''=x'-x'0,
y''=y'-y'0. Yhtälö (5) on
uusissa koordinaateissa x'', y''
.
Se merkitsee vielä
uusia koordinaatteja
x''=x'-x'0,
y''=y'-y'0. Yhtälö (5) on
uusissa koordinaateissa x'', y''
A(x''+x'0)2+B(y''-y'0)2+2C(x''+x'0)(y''+y'0)=G,
joka puolestaan sievenee muotoon
|
Ax''2+By''2+2Cx''y''+2Dx''+2Ey''+F=0.
|
(6) |
Katsotaan vielä, mitä kierto ja siirto tekevät paraabelille (3).
Kierron jälkeen nähdään, että paraabeliin kuuluvat pisteet
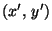 ,
joille pätee
,
joille pätee
eli
Tämä yhtälö on muotoa
Ax'2+By'2+2Cx'y'+D'x'+E'y'=0.
Origon siirto
x''=x'-x0',
y''=y'- y0' johtaa lopulta tasan
samanlaiseen muotoon kuin yhtälössä (6). Mutta mitä on nyt
AB-C2? Se on
Jokaisessa paraabelin kierrosta syntyneessä
käyrän yhtälössä (6) on AB-C2=0.
Ellipsi on yhden määritelmänsä mukaan käyrä, jonka
pisteiden kahdesta kiinteästä pisteestä laskettujen
etäisyyksien summa on vakio, hyperbeli vastaavasti käyrä, jonka
pisteiden kahdesta kiinteästä pisteestä laskettujen
etäisyyksien erotus on vakio. Nämä kaksi kiinteää pistettä
ovat ellipsin tai hyperbelin polttopisteet. Vakiintuneen
merkintätavan mukaan edellä mainittu summa tai erotus on 2a ja
polttopisteet ovat etäisyydellä 2c toisistaan. Ellipsin
tapauksessa on oltava a>c, hyperbelin tapauksessa a<c, tämän
kertoo kolmioepäyhtälö. Toimitaan koordinaatistossa, jossa origo
on polttopisteiden välisen janan keskipiste. Silloin polttopisteet
ovat
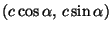 ja
ja
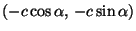 ,
jollakin kulman
,
jollakin kulman 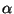 arvolla. Ellipsin määrittelyehto on
arvolla. Ellipsin määrittelyehto on
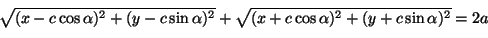 |
(7) |
ja hyperbelin
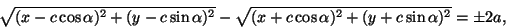 |
(8) |
(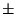 -merkki tarvitaan, koska hyperbelin piste voi olla
lähempänä toista tai toista polttopistettä.) Kun
yhtälöitä (7) ja (8) lähdetään sieventämään, tullaan
ensin yhtälöön
-merkki tarvitaan, koska hyperbelin piste voi olla
lähempänä toista tai toista polttopistettä.) Kun
yhtälöitä (7) ja (8) lähdetään sieventämään, tullaan
ensin yhtälöön
eli
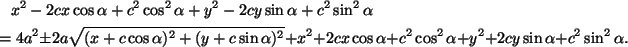
Kun tästä pyyhitään pois samat termit yhtälön molemmilta
puolilta ja vielä jaetaan neljällä, jää lupaavasti vain
Kun vielä korotetaan toiseen potenssiin, saadaan
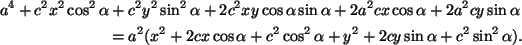
Tässäkin on samoja termejä yhtälön
molemmin puolin! Pyyhitään ne pois ja käytetään tietoa
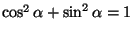 .
Jäljelle jää yhtälö
.
Jäljelle jää yhtälö
Jos otetaan käyttöön merkintä
b2=a2-c2, kun a>c ja
b2=c2-a2, kun a<c, niin on päädytty
ellipsin ja hyperbelin yhtälöihin
tai yhtäpitävästi
Tämähän näyttää aivan samalta kuin aikaisemmin
perusasentoisesta yhtälöstä kiertämällä johdettu
yhtälö. Tarkkaavainen lukija huomaa yhden eron, sillä xy-termit ovat
erimerkkisiä. Sillekin on selityksensä. Aikaisempi yhtälö
lähti siitä, että käyrä ensin oli perusasennossa ja
xy-termin sisältävään yhtälöön päästiin, kun
koordinaatistoa kierrettiin kulman 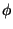 verran. Tämä
jälkimmäinen yhtälö johdettiin suoraan xy-koordinaateissa,
polttopisteiden välinen jana vain oli kulmassa
verran. Tämä
jälkimmäinen yhtälö johdettiin suoraan xy-koordinaateissa,
polttopisteiden välinen jana vain oli kulmassa 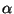 x-akseliin
nähden. Jos alkuperäinen akseli olisi kulkenut polttopisteitten
kautta, olisi xy-koordinaatistoon päästäkseen pitänyt panna
toimeen kierto kulman
x-akseliin
nähden. Jos alkuperäinen akseli olisi kulkenut polttopisteitten
kautta, olisi xy-koordinaatistoon päästäkseen pitänyt panna
toimeen kierto kulman
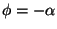 verran. Etumerkkieron selitys on
nyt siinä, että
verran. Etumerkkieron selitys on
nyt siinä, että
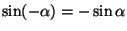 ,
mutta
,
mutta
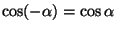 .
.
Minkä kuvion muodostavat ne tason pisteet, jotka toteuttavat
yhtälön
|
Ax2+By2+2Cxy+2Dx+2Ey+F=0?
|
(9) |
Pahimmassa tapauksessa ehdon toteuttavia pisteitä ei ole ollenkaan
tai vain yksi, ja joskus yhtälön vasen puoli saattaa jakautua
kahdeksi ensimmäisen asteen tekijäksi, jolloin yhtälön
toteuttavat kahden eri suoran pisteet. Näitä erikoistapauksia
lukuunottamatta (9) esittää kartioleikkausta. Minkälainen
leikkaus on kyseessä, se nähdään kun koordinaatistoa
kierretään niin, että xy-termi häviää.
Kiertoyhtälöiden
huomioon ottamisen jälkeen (9):n toisen asteen termit ovat
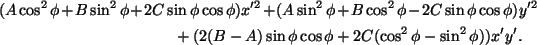
Termin 2x'y' kerroin on
Jos B=A, niin x'y':n kerroin on nolla, kun
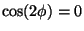 eli kun
eli kun
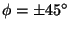 .
Jos
.
Jos 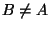 ,
kerroin on nolla, kun
,
kerroin on nolla, kun
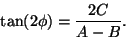 |
(10) |
Kun kiertokulma 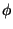 valitaan näin, yhtälön (9) toisen asteen termit ovat
yksinkertaisesti
valitaan näin, yhtälön (9) toisen asteen termit ovat
yksinkertaisesti
A'x'2+B'y'2.
Käyrän olemus selviää
tulosta A'B'. Jos A' ja B' ovat samanmerkkiset, käyrä on
ellipsi, jos erimerkkiset, käyrä on hyperbeli. Jos toinen
kertoimista A', B' on nolla, käyrä on paraabeli. Käyrän
laji määrittyy siis tulosta A'B'. Lasketaan se, kun (10) on
voimassa eli kun pätee
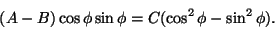 |
(11) |
Kun
käytetään hyväksi yhtälöä (11) ja temppua
saadaan
Yhtälön (9) esittämä käyrä on siis (mainittuja
suoraviivaisia erikoistapauksia lukuun ottamatta) ellipsi, paraabeli
tai hyperbeli sen mukaan, onko AB-C2>0, =0 tai <0.
Solmu 1/2001
2001-04-28


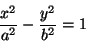
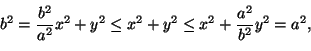
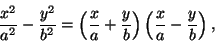
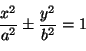
![[kuva]](kiertokuva.png)
![]() ,
niin pisteen P projektio uudella x'-akselilla on C ja uudella
y'-akselilla D. P aseman määrittävät nyt luvut x'=OC=DP ja
y'=OD=CP. Olkoot vielä E ja F pisteen C kohtisuorat projektiot
x-akselilla ja y-akselilla. Mutta
,
niin pisteen P projektio uudella x'-akselilla on C ja uudella
y'-akselilla D. P aseman määrittävät nyt luvut x'=OC=DP ja
y'=OD=CP. Olkoot vielä E ja F pisteen C kohtisuorat projektiot
x-akselilla ja y-akselilla. Mutta
![]() ,
joten
,
joten
![]() .
Vastaavasti
.
Vastaavasti
![]() .
.
![]() kuuluu ellipsiin tai hyperbeliin, jonka yhtälön
voimme kirjoittaa muotoon
kuuluu ellipsiin tai hyperbeliin, jonka yhtälön
voimme kirjoittaa muotoon
![]()
![]() .
Se merkitsee vielä
uusia koordinaatteja
x''=x'-x'0,
y''=y'-y'0. Yhtälö (5) on
uusissa koordinaateissa x'', y''
.
Se merkitsee vielä
uusia koordinaatteja
x''=x'-x'0,
y''=y'-y'0. Yhtälö (5) on
uusissa koordinaateissa x'', y''
![]() ,
joille pätee
,
joille pätee
![]() ja
ja
![]() ,
jollakin kulman
,
jollakin kulman ![]() arvolla. Ellipsin määrittelyehto on
arvolla. Ellipsin määrittelyehto on