

Pekka Kilpeläinen
Kuopion yliopisto
Tietojenkäsittelytieteen ja sovelletun matematiikan laitos
Eräs opiskelija kysyi pitämälläni Algoritmien suunnittelun ja analysoinnin luennolla: "Mitä tekemistä logaritmeilla on tietokoneiden kanssa?" Arvelen hänen kysymyksensä heijastavan sitä monien opiskelijoiden opintoja haittaavaa käsitystä, että matematiikka olisi tietojenkäsittelyn kannalta hyödytöntä. Asia on kuitenkin päinvastoin: matematiikka on tietojenkäsittelyilmiöiden kunnolliselle ymmärtämiselle hyödyllistä ja osin jopa välttämätöntä. Koska lisäksi juuri logaritmifunktio on tietojenkäsittelyn kannalta varsin keskeinen, pyrin valaisemaan kysyttyä asiaa muutamalla yksinkertaisella esimerkillä tiedon esittämiseen tarvittavasta tilasta ja tiedon käsittelemiseen tarvittavasta työmäärästä.
Eksponenttifunktio f(x) = b^x on määritelty kaikilla reaaliluvuilla x ja jokaisella kantalukuna toimivalla positiivisella reaaliluvulla b. Tapaus b=1 on melko mielenkiinnoton, koska 1^x = 1, mutta muulloin b-kantainen eksponentti on injektiivinen ja kaikki positiiviset reaaliarvot saava funktio. (Katso kuva 1.) Positiivisille reaaliluvuille x määritelty logaritmifunktio logb x on tällöin b-kantaisen eksponentin käänteisfunktio, eli logb x on se yksikäsitteinen luku y, jolla b^y = x. Toisin sanoen b^(logb x) = x, eli logb x on se potenssi, johon kantaluku b on korotettava tuloksen x saamiseksi.
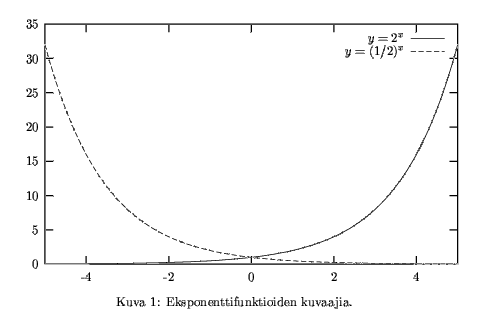
Logaritmi on sikäli mukava operaattori, että se muuttaa argumenttinaan olevan lausekkeen laskutoimituksia helpommiksi: kertolaskusta tulee yhteenlasku (logb (x·y) = logb x + logb y), jakolaskusta tulee vähennyslasku (logb (x/y) = logb x - logb y), ja potenssiinkorotus muuttuu kertolaskuksi (logb (x^y) = y·logb x).
Logaritmin kantaluku voi siis olla melkein mikä tahansa. Matematiikassa tarkastellaan useimmin luonnollista logaritmia ln x = loge x, jonka kantaluku on ns. Neperin luku e ~ 2,718. Luonnontieteissä usein luonteva logaritmin kantaluku on 10, kun taas tietojenkäsittelyssä kaksikantainen logaritmi on usein kätevin. Logaritmin kantaluvulla ei itse asiassa ole kovin suurta väliä: Logaritmifunktiot ovat kasvavia kaikilla ykköstä suuremmilla kantaluvuilla ja poikkeavat tällöin toisistaan vain vakiokertoimella, joka on toisen logaritmin arvo toisen kantaluvusta: loga x = (1/logb a)·logb x. Tämä tarkoittaa esimerkiksi sitä, että kaksikantaisen logaritmin log2 x arvo on luonnollisen logaritmin ln x arvoon verrattuna 1/ln 2- eli likimain 1/0,693 = 1,44-kertainen. (Katso kuva 2.)
Tietojenkäsittelyn kannalta tärkeä logaritmifunktion ominaisuus on sen hidas kasvuvauhti, jonka voi havaita kuvasta 2. Ominaisuutta voi perustella myös logaritmifunktion derivaatalla. Tunnetusti D ln x = 1/x. Derivaatan arvohan annetussa pisteessä vastaa funktion kuvaajalle kyseiseen pisteeseen piirretyn tangentin kulmakerrointa. Suurilla muuttujan x arvoilla logaritmifunktion tangentin kulmakerroin 1/x lähestyy nollaa, eli kuten kuvasta 2 nähdään, logaritmifunktion kasvu alkaa muistuttaa vakiofunktion (olematonta) kasvua. Näemme jatkossa esimerkkejä siitä, että käytännössä esiintyvien lukujen logaritmit ovat usein varsin pieniä. Tästä huolimatta on syytä muistaa, että argumentin kasvaessa myös logaritmifunktion arvo kasvaa rajoittamattoman suureksi.
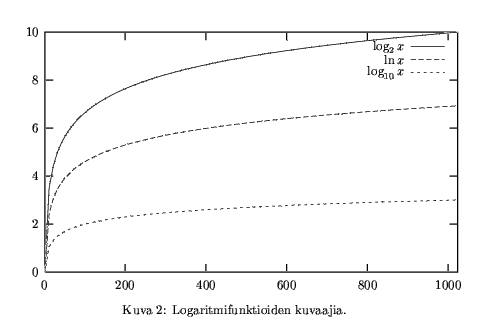
Konkretisoidaan vielä logaritmin kasvuvauhtia muutamalla esimerkillä kaksikantaisesta logaritmista. Eräs perustelu sen hitaalle kasvuvauhdille on edellä mainittu logaritmin kertolaskun yhteenlaskuksi muuttava käyttäytyminen: log2 2x = log2 2 + log2 x = 1 + log2 x. Argumentin kaksinkertaistaminen kasvattaa kaksikantaisen logaritmin arvoa siis vain ykkösellä. Konkreettisina esimerkkeinä todetaan vaikka, että luvun 1000 kaksikantainen logaritmi on hieman alle 10, sillä 2^10 = 1024. (Kaksijärjestelmän keskeisyydestä tietokoneissa johtuu, että yleensä tuhatkertaisuutta tarkoittava etuliite "kilo" tarkoittaa tietotekniikassa juuri arvoa 2^10 = 1024.)
Edelleen on helppo päätellä, että myös miljoonan ja miljardin logaritmit ovat vielä suhteellisen pieniä: log2 1 000 000 = log2 1000^2 = 2·log2 1000 ~ 2·10 = 20, ja log2 10^9 = log2 (1000·10^6) = log2 1000 + log2 1 000 000 ~ 10 + 20 = 30.
Algoritmi kuulostaa lähes samalta kuin "logaritmi": sanat saadaan toisistaan siirtämällä kaksi kirjainta uuteen paikkaan. Mitä sitten algoritmit ovat, ja onko niillä ja logaritmeilla jotain järkevääkin yhteyttä?
Algoritmeilla tarkoitetaan tietojenkäsittelyongelmien täsmällisiä ratkaisumenetelmiä. Jokaisen tietokoneohjelman ytimenä on jonkinlainen algoritmi. Algoritmitutkimus on tietojenkäsittelytieteen keskeinen ala, jonka käytännöllisenä tavoitteena on kehittää tietojenkäsittelyongelmille hyödyllisiä ratkaisualgoritmeja. Tyypillinen tarkastelun kohde on esimerkiksi se, miten tietoa järjestetään tai etsitään tehokkaalla tavalla eri tilanteissa.
Tietokoneohjelmissa tai -laitteissa käyttöön otettavien algoritmien pitäisi olla "hyviä". Algoritmin tulee tietenkin toimia oikein eli suorittaa virheettömästi sitä tehtävää, johon se on kehitetty. Mitä tämän lisäksi pidetään hyvänä voi vaihdella tilanteesta toiseen, mutta yleensä tavoitellaan jossain mielessä tehokkaita ratkaisuja. Tavallisimpia algoritmien tehokkuusmittareita ovat tiedon käsittelyyn tarvittu aika ja toisaalta tiedon esittämiseen tarvittu muistitila. Tehokkaimpia ovat algoritmit, jotka toimivat nopeimmin ja vaativat vähiten muistitilaa.
Yleensä algoritmit ovat ratkaisuja periaatteessa saman ongelman hieman erilaisille ja erikokoisille tapauksille. Ajatellaan esimerkkinä vaikka jonkin henkilön etsimistä puhelinluettelosta. Nimeä voi etsiä täsmälleen samalla tavalla vaikkapa Helsingin, Heinolan tai Hauhon puhelinluettelosta -- yleinen menetelmä toimii kaikissa tapauksissa, vaikka luetteloiden sisällöt ovat aivan erilaiset. Toisaalta nimen etsiminen isommasta luettelosta voi arvatenkin olla työläämpää kuin sen paikantaminen pienemmästä joukosta nimiä. Tämän takia algoritmien tehokkuutta ei ilmoiteta kiinteinä absoluuttisina arvoina.
Algoritmianalyysissä pyritään matemaattisiin lausekkeisiin, jotka kuvaavat algoritmin tekemää työmäärää suhteessa käsiteltävän tapauksen kokoon. Puhelinluetteloesimerkissä luonteva ongelman tapauksen kokoa kuvaava parametri n voisi olla puhelinluettelossa mainittujen nimien lukumäärä. Yksinkertainen (mutta typerä) tapa etsiä annetun henkilön puhelinnumeroa olisi lukea luetteloa alusta alkaen nimi kerrallaan kunnes nimi löytyy tai luettelo loppuu. Pahimmillaan tällaisessa peräkkäishaussa tutkitaan kaikki luettelon n nimeä. Kyseisen algoritmin aikavaativuuden sanotaan olevan lineaarinen (suhteessa nimien lukumäärään n). Luettelon piteneminen kaksinkertaiseksi vaatii peräkkäishaussa pahimmillaan kaksinkertaisen etsintätyön.
Palataan puhelinluetteloetsintään ja sen tehokkaampaan suorittamiseen logaritmisella määrällä suoritusaskeleita hetken kuluttua. Tarkastellaan ensin kokonaislukujen esityksen pituutta, sillä kyseisestä tarkastelusta on hyötyä myös etsintäongelman työläyden arvioinnissa.
Kokonaisluvut ovat keskeisimpiä informaation esittämisen välineitä. Niillä voi laskea lukumääriä tai nimetä mielivaltaisia asioita tyyliin "ensimmäinen", "toinen", jne. Tutustumme nyt kokonaislukujen pituuden ja niiden logaritmien läheiseen yhteyteen.
Tutulla kymmenjärjestelmällä voimme esittää mielivaltaisia kokonaislukuja, vaikka meillä on käytössämme ainoastaan merkit 0, 1, 2, ..., 9. Tämä perustuu käyttämäämme positionaaliseen luvunesitykseen, jossa numerot edustavat sijaintinsa mukaan lukujärjestelmän kantaluvun eri potensseja: vähiten merkitsevät eli oikeanpuoleiset numerot ovat ykkösiä, seuraavat kymppejä, kolmannet satoja jne. Näin esimerkiksi valtion vuoden 2001 budjetin tulojen kokonaismäärä 209 172 310 000 mk tarkoittaa arvoa 0 + 0 · 10 + ... + 1 · 10^4 + 3 · 10^5 + ... + 2 · 10^11 mk.
Kymmenjärjestelmän kantaluku lienee peräisin ihmislajin sormien lukumäärästä. Täsmälleen samaa ideaa voi kuitenkin käyttää myös muilla kantaluvuilla. Jokaisella ykköstä suuremmalla kokonaisluvulla b voidaan nimittäin määritellä b-kantainen lukuesitys (dm-1 dm-2 ... d1 d0)b, missä kukin d0, d1, ..., dm-1 on jokin numeroista 0, 1, ..., b-1. Tällainen luvunesitys tarkoittaa kokonaislukua d0 + d1 · b^1 + ... + dm-2 · b^(m-2) + dm-1 · b^(m-1). Erityisesti tietokoneita on käytännöllistä rakentaa siten, että niiden elektroniikka operoi kymmenen sijasta vain kahdella toisistaan erottuvalla tilalla. Siksi tietokoneet käyttävät binääristä luvunesitystä, jonka kantaluku b on 2 ja jossa käytettävät numerot ovat bittejä 0 ja 1.
Paljonko tilaa kokonaisluvun n esittäminen vaatii? Tarkastellaan kokonaisluvun n esitystä b-järjestelmän lukuna (dm-1 dm-2 ... d1 d0)b. Mitä voidaan sanoa tämän esityksen pituudesta m? Käytetään apuna merkintätapaa, jossa osoitamme jokaisen numeron sijainnin alaindeksinä 0, ..., m-1. Esimerkiksi budjetin loppusumma on tällä esityksellä (211 010 99 18 77 26 35 14 03 02 01 00)10, ja (1m-1 0m-2 ... 00)2 tarkoittaa m-numeroista binäärilukua, jonka merkitsevin numero on ykkönen ja muut nollia.
Jos luku n = (dm-1 dm-2 ... d1 d0)b > 0 on aidosti m-numeroinen, niin sen merkitsevin numero dm-1 on vähintään ykkönen. Siten
Ylläolevan epäyhtälön vasemman puolen arvo on b^(m-1). Soveltamalla epäyhtälöön b-kantaista logaritmia näemme, että m-1 <= logb n, eli esityksen pituus m on enintään logb n + 1. Toisaalta jokainen luvun n numeroista dm-1, ..., d0 on enintään b-1, joten näemme seuraavaa:
| (dm-1 dm-2 ... d1 d0)b | <= | ((b-1)m-1 (b-1)m-2 ... (b-1)1 (b-1)0)b |
| = | (1m 0m-1 ... 01 00)b - 1 | |
| = | b^m - 1 < b^m |
Soveltamalla logaritmia tämän epäyhtälöketjun ensimmäiseen ja viimeiseen jäseneen näemme että logb n < m. Näiden arvioiden mukaan kokonaisluku m on siis suurempi kuin logb n ja enintään logb n + 1. Tämä luku voidaan ilmaista yksinkertaisessa muodossa käyttämällä desimaaliluvun x katkaisevalle alaspäinpyöristykselle merkintää [x]. (Esimerkiksi [2,0] = [2,5] = [2,99] = 2.) Koska desimaaliosan katkaiseminen pienentää lukua alle ykkösellä, on voimassa (logb n) - 1 < [logb n] <= logb n. Lisäämällä tämän epäyhtälön osapuoliin ykkönen nähdään edellisen nojalla, että m = [logb n] + 1. Olemme siis osoittaneet, että kokonaisluvun n esitys b-kantaisessa järjestelmässä on pituudeltaan ykkösen tarkkuudella logb n. Tarkistetaan vielä, että tulos pätee esimerkiksi budjetin loppusummaan n = 209 172 310 000. Nyt 10^11 < n < 10^12, joten [log10 n] + 1 = 11 + 1 = 12, mikä täsmää luvun pituuden kanssa.
Positionaalisen lukuesityksen voimasta ja logaritmisen kasvun hitaudesta saa käsityksen tarkastelemalla vaihtoehtoista unaarista esitystapaa. Unaarinen esitys tarkoittaa alkeellista "tukkimiehen kirjanpitoa", jossa yksinkertaisesti kirjoitetaan peräkkäin esitettävää lukua vastaava määrä ykkösiä.
Kuinka pitkä budjetin loppusumma olisi unaariesityksenä? Arvioidaan, että kirjoitamme noin yhden ykkösen millimetriä kohden. Tällöin budjetin tulojen kokonaismäärän unaariesityksen pituus on noin 209 172,31 km. Tällainen esitys ei mahdu millekään paperiarkille, joten aletaan kirjoittaa sitä vaikka pitkin maantienvartta. Helsingin ja Kilpisjärven välinen etäisyys on Tielaitoksen mukaan 1209 km. Jos aloitamme kyseisen unaariluvun kirjoittamisen tien varteen pääkaupungissa, täytyy Helsinki-Kilpisjärvi-väli kulkea edestakaisin 86 kertaa ja lopuksi matkata vielä kertaalleen Kilpisjärvelle ennenkuin koko luku on kirjoitettu. Valtion budjetin valmistelu unaariluvuin olisi siis ilmeisen hankalaa! Bensaa palaisi, ja tienvartta tallustavien hirvien jäljet sotkisivat laskelmia. Sen sijaan tutussa kymmenjärjestelmässä saman luvun logaritminen pituus on vain 12 numeroa, ja kyseinen summa on siten melko kätevästi hahmotettavissa ja käsiteltävissä.
Ohjelmointikielten toteutukset esittävät kokonaislukuja tyypillisesti yhteen tietokoneen muistisanaan mahtuvina binäärilukuina. Budjetin loppusumma on jo niin suuri luku, että sen binääriesitys ei mahdu tyypillisen modernin tietokoneen 32-bittiseen muistisanaan: edellisen tuloksemme mukaan kyseisen luvun binääriesitys vaatii bittejä [\log2 209172310000] + 1 = 37 + 1 = 38 kappaletta. Budjetin lukuja on siten tietokoneella käsiteltävä esimerkiksi tuhansina markkoina tai käyttäen pidempää, tyypillisesti 64-bittistä kokonaislukujen esitystä.
Tietokoneen muisti koostuu suuresta joukosta yksittäisiä muistitavuja. Jokaisella muistitavulla on osoitteenaan ei-negatiivinen kokonaisluku, jota prosessori käsittelee osoiterekisterissään. Suurin n-bittiseen osoiterekisteriin mahtuva binääriluku on (1n-11n-2... 10)2, jonka arvo on 2^n - 1. Tällöin kone voi käyttää 2^n-tavuisen keskusmuistin muodostamaa osoiteavaruutta numeroimalla muistitavut 0, 1, ..., 2^n - 1. Osoiterekisterin pituuden on siis oltava vähintään kaksikantainen logaritmi koneen osoiteavaruuden koosta. Tyypillinen osoiterekisterin pituus on 32 bittiä, mikä riittää toistaiseksi hyvin nykyisten tietokoneiden osoiteavaruuksille aina neljään gigatavuun (4·2^30 = 2^32) saakka. Keskusmuistien jatkuvasti kasvaessa osoiterekisterien kuitenkin odotetaan jatkossa pitenevän esimerkiksi 40-bittisiksi.
Ihminen etsii nimeä puhelinluettelosta jotakuinkin seuraavasti: Luettelo avataan niiltä paikkeilta missä nimen arvellaan esiintyvän. Korhonen löytyisi luultavasti luettelon keskivaiheilta, kun taas vaikkapa Ylppöä kannattaisi etsiä loppupuolelta. Jos haettu nimi edeltää aakkosjärjestyksessä avatun sivun sisältöä, etsintä kohdistetaan seuraavaksi luettelon avaamiskohtaa edeltävään osaan. Päinvastaisessa tapauksessa etsintää jatketaan vastaavasti avaamiskohtaa seuraavasta luettelon osasta. Haettu nimi löytyy parhaimmillaan jo ensimmäisiltä avatuilta sivuilta, mutta muussa tapauksessa samaa avauskohdan etu- tai takapuolelta hakemista jatketaan kunnes nimi löytyy tai selviää, että haettua numeroa ei ole luettelossa.
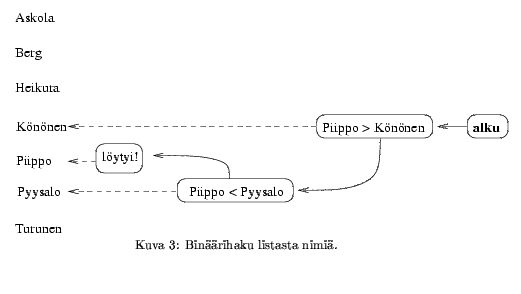
Samaan menetelmään perustuu yleinen binäärihaun nimellä tunnettu algoritmi. Haettavan arvon -- edellä nimen -- etsintä järjestyksessä olevien arvojen jonosta aloitetaan tutkimalla jonon keskimmäistä alkiota. (Jos jonon pituus on parillinen, täsmällisen algoritmin täytyy päättää, kumpaa keskimmäisistä alkioista tutkitaan.) Jos arvo löytyy, etsintä päättyy onnistuneesti. Muuten täsmälleen samaa metodia sovelletaan jonon alku- tai loppupuoliskoon sen mukaan, havaittiinko etsittävä arvo pienemmäksi vai suuremmaksi kuin jonon keskeltä tutkittu alkio. Kuvassa 3 on esimerkki binäärihausta etsittäessä nimeä "Piippo" aakkosjärjestyksessä olevien nimien listasta.
Binäärihaku on erittäin tehokas tapa etsiä tietoa, mikä nähdään seuraavasti: Tarkastellaan työläintä tilannetta, jossa alkio löytyy (tai sen puuttuminen havaitaan) vasta kun etsittävä jono on toistuvien puolitusten tuloksena kutistunut yhdeksi ainoaksi alkioksi. Jos ensimmäinen vertailu tutkii n-alkioisen jonon keskialkiota, seuraavalla kerralla jonon pituus on puolittunut arvoon n/2, sitten arvoon n/4, ja niin edelleen, kunnes jäljellä on vain yksi alkio. Montako tällaista vaihetta tarvitaan? Ajattellaanpa prosessia takaperin: montako kertaa ykkösen mittaisen jonon pituutta on kaksinkertaistettava, jotta saadaan vähintään alkuperäisen n pituinen jono? Kysymys on lähes sama kuin "montako kertaa luku 2 on kerrottava itsellään, jotta saadaan luku n", joten vastaus on likimain log2 n + 1.
Olisiko järjestetystä jonosta etsintää mahdollista suorittaa binäärihakua oleellisesti tehokkaammin? Vastaus on kielteinen, ainakin sellaisten algoritmien osalta, joiden toiminta perustuu etsittävän arvon ja jonon alkioiden välisiin vertailuihin. (Vaihtoehtoisena strategiana voisi ajatella esimerkiksi yritystä laskea haettavan arvon mahdollinen sijaintipaikka hyödyntäen jonkinlaisia jonon arvojakaumaa kuvaavia tietoja.) Binäärihaun optimaalisuus voidaan perustella seuraavasti.
Tietokoneohjelmat käsittelevät järjestettyjä jonoja taulukoina, joitten alkioihin viitataan niiden järjestysnumerolla. Ajatellaan arvojen välisiin vertailuoperaatioihin (<, <=, =, >= ja >) perustuvaa proseduuria Search, joka saa syötteenään järjestetyn n-alkioisen taulukon sekä siitä etsittävän arvon x. Proseduuri palauttaa taulukon alkion järjestysnumeron k = 1, ..., n, jos etsitty arvo x löytyy taulukossa paikasta k. Mikäli arvoa ei löydy, Search palauttaa arvon 0.
Montako vertailuoperaatiota proseduuri Search joutuu enimmillään suorittamaan? Jokainen hyödyllinen vertailu voi olla tosi tai epätosi eli tuottaa täsmälleen yhden bitin verran informaatiota haetun arvon sijainnista taulukossa. Erisuuruusvertailut <, <=, >= ja > kertovat täytyykö etsityn arvon löytyä vertailukohdan etu- vai takapuolelta, ja yhtäsuuruusvertailu viimeiseksi vaihtoehdoksi jääneen alkion kanssa ilmoittaa, löytyykö arvo tutkitusta paikasta vai puuttuuko se taulukosta kokonaan.
Proseduurin tulosarvoa k voi nyt ajatella arvojen 0, ..., n esittämiseen riittävän pituisena binäärilukuna, jonka kutakin bittiä vastaa yksi algoritmin suorittama vertailu. Kuten edellä näimme, tämän luvun pituus on [log2 n] + 1, joten Search-proseduuri joutuu väistämättä joskus suorittamaan näin monta vertailuoperaatiota.
Vaikka binäärihaun tehokkuuden ja binääriluvun pituuden välinen yhteys on kiinnostava, algoritmin työmäärän analysointi näin tarkasti, yksittäisten suoritusvaiheitten tarkkuudella, on usein tarpeetonta. Oleellisempaa on algoritmin suoritustehon karkea riippuvuus käsiteltävien syötteiden koosta. Edellä tarkastellun logaritmien hitaan kasvuvauhdin ansiosta binäärihaun kaltaiset logaritmisessa ajassa toimivat algoritmit ovat erittäin tehokkaita. Niiden tietokonetoteutukset suoriutuvat käytännössä ratkottavista tapauksista silmänräpäyksessä eivätkä hidastu havaittavasti, vaikka käsiteltävät syötteet pitenisivät moninkertaisiksi.