PDF, PS

HTKK, TTKK, LTKK, OY, ÅA/Insinööriosastot
Valintakuulustelujen matematiikan koe 2.6.1999
Ratkaisut

1. Välttämätön ja riittävä ehto on, että kätrillä on korkeintaan yksi leikkauspiste, ts. että yhtälöllä

x² + 3ax = x³ - 2x² + 3x

on korkeintaan yksi ratkaisu. Selvästi x=0 on yhtälön ratkaisu (riippumatta vakion a arvosta), ja sieventämällä yhtälö saadaan seuraava ehto: käyrät eivät rajoita äärellisiä tasoaluetta jos ja vain jos yhtälöllä

$$x^{2} - 3x + 3 - 3a = 0 \qquad(1)$$

ei ole reaalisia ratkaisuja paitsi mahdolisesti x=0. Jos x=0 olisi yhtälön (1) ratkaisu, niin x=3 olisi myös ratkaisu. Siis ainoa mahdollisuus on, että yhtälöllä (1) ei ole ollenkaan reaalisia ratkaisuja, jolloin diskriminantin on oltava aidosti negatiivinen:

$$3^{2} - 4(3 - 3a) < 0 \qquad eli \qquad \mathbf{a} < \frac{1}{4}$$

2. Auringonsäteiden suuntainen pylvään huipun kautta kulkeva suora toteuttaa yhtälöryhmän

$$\frac{x}{-1} = \frac{y}{-2} = \frac{z-12}{7/5}.$$

Kyseisen suoran ja seinän leikkauspiste toteuttaa lisäksi seinän yhtälön $y = \frac{6}{5}x + \frac{37}{7}$, ja näiden yhtälöiden ratkaisuna saadaan leikkauspisteen koordinaatit $x = \frac{185}{28}$, $y = \frac{185}{14}$ ja $z = \frac{11}{4} = 2.75$. Siis varjon huippu on seinällä korkeudella

$$\mathbf{2 \quad m \quad 75 \quad cm.}$$

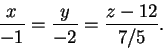
3. Sarja on geometrinen suhdelukuna $\frac{-3}{x}$, joten se suppenee jos ja vain jos pätee $\left\vert \frac{-3}{x} \right\vert < 1$ eli $\left\vert x \right\vert > 3$. Sarjan summa on tällöin $\frac{1}{1 + \frac{3}{x}} = \frac{x}{x+3}$. Yhtälön

$$\frac{3x+8}{x+1} = \frac{x}{x+3} \qquad eli \qquad x^{2} + 8x + 12 = 0$$

ratkaisut ovat x = -2 ja x = -6. Pisteessä x = -2 sarja hajaantuu, joten tehtävällä on yksikäsitteinen ratkaisu x = -6.

4. (Huom: $\log_2 x = \frac{\ln x}{\ln 2}$.)

Funktio E on derivoituva välillä 0 < p < 1, ja

$$E'(p) = - \log_2 p - p\frac{1}{p \ln 2} + \log_2 (1-p) + (1+p)\frac{1}{(1-p)\ln 2} = \log_2 (\frac{1-p}{p}).$$

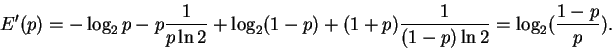
Siis E'(p) = 0 jos ja vain jos $\frac{1-p}{p} = 1$ eli $p = \frac{1}{2}$.

Selvästi E'(p) > 0 kun 0 < p < $\frac{1}{2}$, ja E'(p) < 0 kun $\frac{1}{2}$ < p < 1, joten

p = $\frac{1}{2}$ on todella funktion E maksimikohta välillä 0 < p < 1.

Kysytty maksimiarvo on E $(\frac{1}{2}) = -\frac{1}{2} \log_2 (\frac{1}{2}) - \frac{1}{2} \log_2 (\frac{1}{2}) = \frac{1}{2} + \frac{1}{2} = \mathbf{1}$.

5. Kuution särmän pituuden x on oltava jaollinen luvuilla 7, 11 ja 13. Koska näillä ei ole yhteisiä tekijöitä, pienin mahdollinen x:n arvo on x=7 $\cdot$ 11 $\cdot$ 13 = 1001. Pienimmän mahdollisen kuution tilavuus on siten 1001³. Yhden rasian tilavuus on 1001, joten (pienin mahdollinen) rasioiden lukumäärä on

$$\frac{1001^{3}}{1001} = 1001^{2} = \mathbf{1002001}.$$

6. a) On näytettävä, että jos x(t) = 0 niin y(t) = H.

Jos x(t) = 0, niin $t = \frac{R \sin \alpha}{v \cos \alpha}$; sijoittamalla tämä sekä tehtävässä annetut a

ja p saadaan

$$y(t) = R\cos \alpha + vt\sin \alpha - (1/2)gt^{2} = \ldots = ... ...rac{a}{2} + \frac{1}{p} - \frac{a}{2p^{2}} ) = H. \quad m.o.t.$$

b) On määriteltävä suurin nopeus v (tai vastaavasti pienin vakion a arvo), jolla H $\le$ 1.9 R kaikilla kulmilla $\alpha$ (eli kaikilla suureen p arvoilla, 0 < p $\le$ 1).