Otsikkokuva

Tehtävien ratkaisut

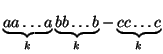1. Merkitään $\underbrace{aa\ldots a}_{k} \underbrace{bb\ldots b}_{k}-\underbrace{cc\ldots c}_{k}$ , missä a, b ja c ovat kokonaislukuja. Tällöin

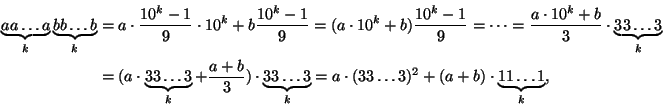
$\begin{displaymath}\begin{split} \underbrace{aa\ldots a}_{k}\underbrace{bb\ldots... ...3\ldots3)^2+(a+b)\cdot \underbrace{11\ldots 1}_{k}, \end{split}\end{displaymath}$

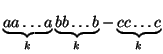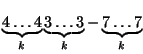eli jos a=1, a=4 tai a=9 ja c= $a+b\le 9$ , niin $\underbrace{aa\ldots a}_{k} \underbrace{bb\ldots b}_{k}-\underbrace{cc\ldots c}_{k}$ on neliö. Esimerkiksi $\underbrace{4\ldots 4}_{k}\underbrace{3\ldots 3}_{k}- \underbrace{7\ldots 7}_{k}$ on neliö.

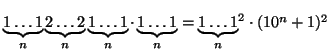a): $\underbrace{1\ldots 1}_{n} \underbrace{2\ldots 2}_{n}\underbrace{1\ldots 1}_{n}\cdot \underbrace{1\ldots 1}_{n} = {\underbrace{1\ldots 1}_{n}}^2\cdot (10^n+1)^2$ ,
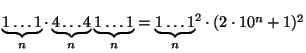b): $\underbrace{1\ldots 1}_{n}\cdot\underbrace{4\ldots 4}_{n} \underbrace{1\ldots 1}_{n} = {\underbrace{1\ldots 1}_{n}}^2\cdot (2\cdot 10^n+1)^2$ , ja
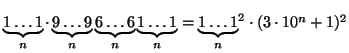c): $\underbrace{1\ldots 1}_{n}\cdot\underbrace{9\ldots 9}_{n} \underbrace{6\ldots 6... ...erbrace{1\ldots 1}_{n} = {\underbrace{1\ldots 1}_{n}}^2\cdot (3\cdot 10^n+1)^2$ .

3. Luku on 4:llä jaollinen, joten ainoat mahdollisuudet ovat b=0, 4 tai 8. Jos b=0, niin 3:lla jaettaessa saadaan $\frac{a000}{3}$ , joten a=3 tai 9. Jos b = 4, niin vastaavalla tavalla saadaan a=1, 4 tai 7, ja jos b = 8, niin a = 2, 5 tai 8. Jaettaessa 11:llä jakojäännös on 10, joten jäljelle jää vain yksi mahdollisuus 1044.

4. Kaavaa (a-1)(a²+a+1)=a³-1 käyttäen saamme esimerkiksi

$\begin{displaymath}(a^2+a+1)(a^6+a^3+1)(a^{18}+a^9+1)(a^{54}+a^{27}+1) =\frac{a^{3^4}-1}{a-1}=1+a^2+\cdots+a^{80}, \end{displaymath}$

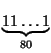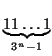joka on $\underbrace{11\ldots 1}_{80}$ silloin kun a=10. Yleisessä tapauksessa saamme vastaukseksi $\underbrace{11\ldots 1}_{3^n-1}$ .

5. Yhtälöksi saadaan $(a^2+b^2)m=a\cdot 10+b$ , missä a, b ja m ovat kokonaislukuja. Tästä seuraa, että

a² m-10a+b² m-b=0

ja siis

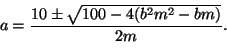
$\begin{displaymath}a=\frac{10\pm\sqrt{100-4(b^2 m^2-bm)}}{2m}. \end{displaymath}$

Merkitään k=bm, jolloin k on kokonaisluku. Lausekkeen $\sqrt{100-4k(k-1)}$ täytyy olla kokonaisluku, joten kokeilemalla k:n arvoja 0, 1, 2, 3, 4 ja 5 nähdään, että ainoa mahdollisuus on k=bm=0. Näin ollen b=0, sillä $m\neq 0$ . Sijoittamalla saamme

$\begin{displaymath}a=\frac{10+10}{2m}=\frac{10}{m}\quad\text{ja siten}\ a=1,\ 2,\ \text{tai}\ 5, \end{displaymath}$

joten kysytty ominaisuus on vain kolmella luvulla 10, 20 ja 50:

$\begin{displaymath}\frac{10}{1^2+0^2}=10,\quad \frac{20}{2^2+0^2}=5\quad\text{ja}\quad \frac{50}{5^2+0^2}=2. \end{displaymath}$

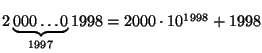6. Koska $2\underbrace{000\ldots 0}_{1997}1998 = 2000\cdot10^{1998}+1998$ ja 1999 on alkuluku, jolle $\varphi(1999)=1998$ , saamme Fermat'n lausetta käyttäen tulokseksi $1\cdot1-1\equiv 0\,(\text{mod}\,1999)$ .

7. Tutkitaan lukua

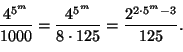
$\begin{displaymath}\frac{4^{5^m}}{1000} =\frac{4^{5^m}}{8\cdot 125} =\frac{2^{2\cdot 5^m-3}}{125}. \end{displaymath}$

Vihjeen mukaan $1\equiv 2^{\varphi(125)}\,(\text{mod}\,125)$ , missä

$\begin{displaymath}\varphi(125)=125-25=100, \end{displaymath}$

sillä luvuista $1,2,\ldots,125$ ainoastaan luvuille $m=5,10,15,\ldots,120,125$ on $\text{syt}\,(m,125)>1$ , ja näitä on 25 kappaletta. Tästä seuraa, että $2^{100}\equiv 1\,(\text{mod}\,125)$ , ja toisaalta $5^m\equiv 25\,(\text{mod}\,100)$ , kun $m\ge 2$ . Tätä tietoa käyttäen saamme

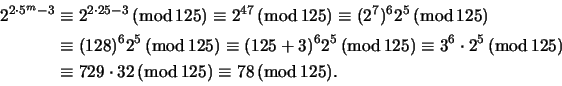
$\begin{displaymath}\begin{split} 2^{2\cdot 5^m-3}\,(\text{mod}\,125)&\equiv 2^{2... ...32\,(\text{mod}\,125) \equiv 78\,(\text{mod}\,125). \end{split}\end{displaymath}$

Näin ollen luvun 4^{5^m}, $m\ge 2$ , kolme viimeistä numeroa ovat $78\cdot 8=624$ , koska $125\cdot 8=1000$ ja 624<1000.

Djemil Mamedjarov

Matematiikkalehti Solmu
2000-11-16