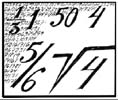
Vaikka normaaliin kirjoitusjärjestelmäämme kuuluvat arabialaiset numerot 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 ovat saavuttaneet jokseenkin universaalin aseman, roomalaista lukumerkintää näkee yhä kellotauluissa, juhlallisesti ilmaistuissa vuosiluvuissa, kuninkaallisten nimissä (Kaarle XVI Kustaa), joskus amerikkalaisissa vähemmänkin kuninkaallisissa nimissä (Henry Ford III), kirjojen lukujen tai osien järjestysnumeroissa sekä ulkomaalaisten kirjojen esipuheosaston sivunumeroissa. Myös lääkeresepteissä on tapana ilmoittaa annoskoko roomalaisin numeroin.
Roomalaisen numerojärjestelmä perusajatus on yhteenlasku. Se on sama kuin sormilla laskemisen tai helmitaulun tai tukkimiehen kirjanpidon: numeroa esitetään yhtä monella merkillä kuin numeron esittämä luku ilmaisee. Siten 1 = I, 2 = II, 3 = III, 4 = IIII. Koska lukujen kasvaessa menettely tulee kömpelöksi, otetaan käyttöön lyhennysmerkinnät 5 = V, 10 = X, 50 = L, 100 = C, 500 = D ja 1000 = M. Joidenkin käsitysten mukaan viiden kymmenmonikertoja edustavat V, L ja D olisivat peräisin muinaisten roomalaisten naapureilta, sittemmin roomalaisiin sulautuneilta etruskeilta.
Antiikin roomalaiset muodostivat numeronsa yksinkertaisesti kirjoittamalla näitä merkkejä peräkkäin tarvittavan määrän. Siten esim. 90 = DXXXX ja 1492 = MCCCCLXXXXII. Keskiajalla tuli kuitenkin käyttöön lyhennysmerkintä, jota nykyäänkin sovelletaan. Siinä symbolit I, X ja C kirjoitettuna jomman kumman välittömästi suuremman symbolin eteen tulkitaan vähentävästi. Siis IV = 4, IX = 9, XL = 40, XC = 90, CD = 400 ja CM = 900. Siis 19 = XIX, 49 = XLIV, 1999 = MCMXCIX, 1492 = MCDXCII. Nämä nykyisin "oikeiksi" kiteytyneet käsitykset roomalaisista numeroista ovat vähän liiankin selkeitä. Tosiasiassa merkintätavat ovat olleet huomattavasti kirjavampia ja käytössä olleiden numeromerkkien valikoimakin suurempi.
Roomalaiset numerot eivät nykyään esiinny yhteyksissä, joissa niillä pitäisi suorittaa laskutoimituksia. Mutta toki roomalaisilla numeroilla on laskettu - käytiinhän antiikissakin kauppaa ja kerättiin veroja. Yhteenlasku alkuperäisillä antiikin merkinnöillä on helppoa: kirjoitetaan vain yhteenlaskettavien merkit peräkkäin ja yhdistetään viiden niput: 434 + 136 = CCCCXXXIIII + CXXXVI = CCCCCXXXXXXVIIIII = DLXVV = DLXX. Huomaa, että et tässä tarvitse sellaisia ala-asteella tai aikaisemmin ulkoa oppimiasi asioita kuin 6 + 4 = 10 tai 3 + 3 = 6. Jos käytetään "modernimpaa" merkintää, täytyy ottaa huomioon sievennyssääntö: vähentävän I:n, X:n tai C:n kompensoi vastaava lisäävä merkki. Siis CDXXXIV + CXXXVI = CDCXXXXXXIVVI = DXXXXXXVV = DLXX.
Roomalaisten numeroiden kertolasku on helpointa hahmottaa helmitaulunomaisella menetelmällä. Tämä on erityisen selkeää, jos kerrottavassa ja kertojassa ei esiinny yhtä aikaa "etruskimerkkejä" V, L tai D. Tällöin riittää, kun kirjoitetaan kerrottavan ja kertojan "MDCLVI-rakenteet" allekkain käyttämällä jotain laskumerkkiä, vaikkapa x:ää. Jokaista kertojan kaaviossa olevaa merkkiä kohden kirjoitetaan kerrottavan rakenne alkamaan oikealta tämän merkin kohdalta. Lasketaan samassa pystyrivissä olevat merkit yhteen ja sievennetään tarpeen mukaan. Tarkastetaan esimerkkinä kertolaskua XXVI kertaa CXXI eli 26×14.

Etruskimerkkien keskinäinen kertolasku vaatii oman
sääntönsä. Tällaisessa kertolaskussa kirjoitetaan asianomaiseen
sarakkeeseen edelleen yksi laskumerkki, mutta sen lisäksi seuraavaan
vasemmanpuoleiseen kaksi merkkiä. Lasketaan VI kertaa XVI eli 6×16
ja käytetään etruskilukuihin liittyvänä laskumerkkinä selvyyden
vuoksi y:tä. Symbolit y ja x ovat kuitenkin ihan samanarvoisia.
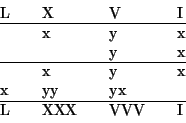
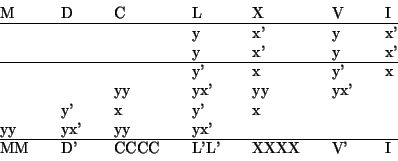
Jos luvuissa käytetään vähennysmerkintöjä kuten IX tai
XL, tarvitaan vielä yksi sääntö. Tällöin merkitään
vähentävien symbolien sarakkeeseen esimerkiksi ':lla täydennetty
laskumerkki. Jos kertojasarakkeessa on tällainen merkki, kerrottavan
siirrossa jokainen pilkuton merkki muutetaan pilkulliseksi ja pilkullinen
pilkuttomaksi. Yhteenlaskussa pilkullinen ja pilkuton merkki kumoavat
toisensa. Esimerkki XLIV kertaa XLIV eli 442 valaisee asiaa:
Tuntuuko mutkikkaalta? Ehkä tämä onkin hankalaa, mutta toisaalta huomaat, että kertolaskun olennaista apuvälinettä, kertotaulua, et tarvitse ollenkaan. Jos siis huomaat, että sellaisen tiedon kuin 7×6=42 tai 8×7=56 tallentaminen päässä on työlästä, voit yrittää ruveta laskemaan roomalaisin numeroin!
Entä jakolasku? Jakolasku perustuu siihen, että selvitetään
montako kertaa jakaja voidaan vähentää vähennettävästä.
Lasketaan esimerkiksi CCCLXXVII jaettuna XV:llä.
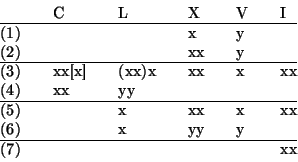
Roomalaisen numerojärjestelmän perusajatus, lukuun sisältyvien kymmenpotenssien lukumäärän ilmaiseminen kutakin kymmenpotenssia vastaavan merkin lukumäärällä, esiintyy monissa eri kulttuureissa, jo egyptiläisestä hieroglyfikirjoituksesta alkaen. Muinaiskreikkalaisten kahdesta lukujärjestelmästä toinen, ns. attikalainen järjestelmä, on hyvin samanlainen kuin roomalaisten lukujärjestelmä. Eri kulttuureissa esiintyi myös toisenlaisia lukujenmerkitsemisajatuksia. Muinaisessa Kaksoisvirtainmaassa, nuolenpääkirjoituksen alueella, tuli käyttöön järjestelmä, jossa luvuille 1, ..., 59 oli kullekin oma merkkinsä, mutta luvuille 60 ja 602 käytettiin samaa merkkiä kuin luvulle 1, ja kaksi rinnakkain olevaa ykkösen ja kakkosen merkkiä tarkoitti joko lukua 62=1×60+2 tai 121=2×60+1. Tämä on varhaisin paikkajärjestelmä, lukujärjestelmä, jossa sama merkki tarkoittaa eri lukua riippuen siitä, missä asemassa se on muihin numeromerkkeihin nähden. Muinaisilla kiinalaisilla oli käytössä lähes nykyaikainen paikkajärjestelmä, joka kuitenkin toimi niin, että ykkösiä osoittavat merkit saattoivat osoittaa myös satoja, kymmeniä tuhansia jne., kun taas kymmeniä osoittavat merkit tarkoittivat myös tuhansia ja satoja tuhansia.
Meidän kymmenjärjestelmämme juuret johtavat Intiaan, jossa ainakin jo varhaiskeskiajalla noin 500 jKr. oli käytössä paikkajärjestelmä, jossa alkuun yhdeksällä numeromerkillä osoitettiin kaikki positiiviset luvut. Näillä luvuilla laskeminen vaati omat tekniikkansa - ja kertotaulun. Tärkeän palveluksen intialaisten numeroiden maailmanvalloitusmatkalle teki Bagdadissa 800-luvun alkupuolella vaikuttanut Muhammad ibn Musa Al-Khowarizmi. Hän kirjoitti arabian kielellä intialaisten numeroiden käyttöoppaan, joka myöhemmin käännettiin latinaksi. Al-Khowarizmin nimi vääntyi muotoon algorismi, jolla tarkoitettiin uutta tapaa laskea, ja intialaisista numeroista alettiin puhua arabialaisina. (Al-Khowarizmin kirjan latinankielinen nimi oli kyllä De numero indorum) Ei ole vaikea tunnistaa Al-Khowarizmista myös algoritmi-sanan alkuperää.
Nyt päättymässä olevan vuosituhantemme (sehän kaikesta millenniumkohusta huolimatta päättyy vasta vuoden 2000 lopussa!) ensimmäisten vuosisatojen aikana uutta laskutapaa kannattaneet algoristit ja roomalaisia numeroita sekä helmitaulun eli abakuksen käyttöä puolustaneet abbakistit kiistelivät menetelmien paremmuudesta. Algoristien voitto tuli hitaasti - ennakkoluulot olivat voimakkaita. Vielä vuonna 1299 annettiin Firenzessä asetus, joka kielsi rahanvaihtajia käyttämästä liiketoimissaan arabialaisia numeroita.
Matti Lehtinen