Tehtävät

1. Määritä kaikki äärelliset tasojoukot S, joissa on vähintään kolme pistettä ja jotka täyttävät seuraavan ehdon: kun A ja B ovat joukon S kaksi eri pistettä, joukko S on symmetrinen janan ABkeskinormaalin suhteen.

2. Olkoon n kiinteä kokonaisluku, jolle $n\geq 2$.
(a) Määritä pienin sellainen vakio C, että kaikilla reaalisilla $x_1,\ldots,x_n\geq 0$ pätee epäyhtälö

$$\sum_{1\leq i < j \leq n} x_i x_j(x_i^2 + x_j^2) \leq C\Big( \sum_{1\leq i \leq n} x_i\Big)^4.$$

(b) Määritä, milloin yhtäsuuruus on voimassa, kun C on kuten yllä.

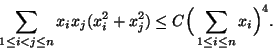
3. Tarkastellaan $n\times n$-lautaa, missä n on kiinteä positiivinen parillinen kokonaisluku. Lauta koostuu n² yksikköruudusta. Kahden eri ruudun sanotaan olevan vierekkäiset, jos niillä on yhteinen sivu.

Laudan N ruutua merkitään niin, että jokaisen laudan (merkityn tai merkitsemättömän) ruudun vieressä on vähintään yksi merkitty ruutu.

Määritä luvun N pienin mahdollinen arvo.

4. Määritä kaikki sellaiset positiivisten kokonaislukujen parit (n,p), että p on alkuluku, $n\leq 2p$ ja (p-1)ⁿ + 1 on jaollinen luvulla n^p-1.

5. Ympyrät $\Gamma_1$ ja $\Gamma_2$ sisältyvät ympyrään $\Gamma$ ja sivuavat ympyrää $\Gamma$eri pisteissä M ja N. Ympyrä $\Gamma_1$ kulkee ympyrän $\Gamma_2$ keskipisteen kautta. Ympyröiden $\Gamma_1$ ja $\Gamma_2$ leikkauspisteiden kautta kulkeva suora leikkaa ympyrän $\Gamma$ pisteissä A ja B. Suorat MA ja MB leikkaavat ympyrän $\Gamma_1$pisteissä C ja D.

Todista, että suora CD sivuaa ympyrää $\Gamma_2$.

6. Määritä kaikki sellaiset kuvaukset $f:\mathbb{R}\to \mathbb{R}$, että jokaisella $x,y\in\mathbb{R}$ on voimassa yhtälö

$$f(x-f(y))=f(f(y)) + x\,f(y)+f(x)-1.$$