Geometriakulma: Ellipsin parametriesitys ja mitä sillä voi tehdä

Palattakoon aluksi viidenteen geometriakulmaan ja ellipsin piirtämiseen pisteittäin:

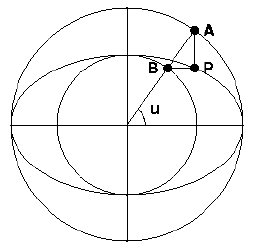
Asettamalla ellipsin keskipisteestä säde, joka leikkaa a- ja b-säteiset ympyrät pisteissä A ja B, löydetään kuvan konstruktiolla ellipsin piste P. Jos säteen suuntakulma on u, saadaan trigonometrian avulla pisteen P = (x,y) koordinaateille

$$x = a\cos u, \qquad y = b\sin u.$$

Koko ellipsi saadaan, kun annetaan kulmalle u arvot täyden kierroksen alueelta $[0,2\pi[$.

On saatu ellipsin parametriesitys: Jokaisen ellipsin pisteen paikkavektori, so. keskipisteestä ellipsin pisteeseen osoittava vektori voidaan esittää muodossa

$$\vec{r}(u) = a\cos u \,\vec{i} + b\sin u \,\vec{j}, \quad 0 \le u < 2\pi.$$

Muuttujaa u kutsutaan parametriksi tai ellipsin tapauksessa (muitakin käyriä voidaan nimittäin tarkastella niiden parametriesityksen avulla) myös nimellä eksentrinen anomalia.

Paikkavektorin derivaatta

$$\vec{t}(u) = \vec{r}\ {}'(u) = \lim_{h \rightarrow 0} \frac{\... ...u+h) - \vec{r}(u)}{h} = - a\sin u\,\vec{i} + b\cos u \,\vec{j}$$

antaa ellipsin tangenttivektorin. Erotusosamäärävektori $[\vec{r}(u+h) - \vec{r}(u)]/h$ on nimittäin parametriarvoja u+h ja u vastaavien pisteiden välisen jänteen suuntainen ja rajaprosessissa $h \rightarrow 0$ pisteet lähestyvät toisiaan, jolloin jänne kääntyy tangentin suuntaiseksi.

Parametriesityksen avulla voidaan helposti osoittaa ellipsin heijastusominaisuus: jos polttopisteestä lähtenyt säde heijastuu ellipsin kehästä heijastumislain mukaisesti, se kulkee toisen polttopisteen kautta. Tämän näyttämiseksi riittää laskea polttopisteistä ellipsin pisteeseen osoittavien vektoreiden ja tangenttivektorin väliset kulmat ja todeta nämä yhtä suuriksi.

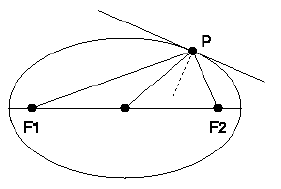
Polttopisteistä F₁ = (-c,0) ja F₂ = (c,0) parametriarvoa uvastaavaan ellipsin pisteeseen osoittavat vektorit ovat

$$\vec{p}_1 = (a\cos u + c)\vec{i} + b\sin u \,\vec{j} \quad\hbox{ja}\quad \vec{p}_2 = (a\cos u - c)\vec{i} + b\sin u \,\vec{j}.$$

Näiden pituudet ovat $\vert\vec{p}_1\vert = a + c\cos u$ ja $\vert\vec{p}_2\vert = a - c\cos u$; lasku, joka on melko suoraviivainen, mutta jossa tarvitaan ellipsille karakteristista yhtälöä a² = b² + c², jääköön lukijan suoritettavaksi.

Tangenttivektorin $\vec{t}(u)$ ja vektoreiden $\vec{p}_1$ ja $\vec{p}_2$välisten kulmien kosinit saadaan lausekkeista

$$\frac{\vec{t} \cdot \vec{p}_1}{\vert\vec{t}\,\vert\,\vert\vec... ...t} \cdot \vec{p}_2}{\vert\vec{t}\,\vert\,\vert\vec{p}_2\vert}.$$

Laskemalla saadaan - yksityiskohdat jääkööt taas lukijalle -

$$\frac{\vec{t} \cdot \vec{p}_1}{\vert\vec{p}_1\vert} = - c\sin... ...\frac{\vec{t} \cdot \vec{p}_2}{\vert\vec{p}_2\vert} = c\sin u.$$

Tällöin kosinit ovat vastalukuja ja niitä vastaavat kulmat siis muotoa $\alpha$ ja $180^{\circ} - \alpha$, mikä vektoreiden suunnat huomioon ottaen merkitsee juuri heijastumislain mukaista tilannetta.

Simo K. Kivelä

Solmu 1/1999-2000
Viimeksi muutettu 4.4.2000