Solmun tehtävät

Solmun tehtävät 41 - 46 esitettiin numerossa 2/98-99. Immo Heikkinen lähetti hyvät ratkaisut kaikkiin kuuteen tehtävään, ja ne julkaistaan tässä.

41. Luku $110\,355\,024$ on neljän peräkkäisen positiivisen kokonaisluvun tulo. Mitkä nämä luvut ovat?

Immo Heikkisen ratkaisu. Koska $\root 4\of{110\,355\,024}\approx 102{,}5$, ilmeisiä ehdokkaita kysytyiksi luvuiksi ovat 101, 102, 103 ja 104. Kertolasku osoittaa, että luku todella on $101\cdot 102\cdot 103\cdot 104$. - Toinen hyvä vinkki (joka toimii ilman juurenottoja, jotka vaativat laskimen tai kohtuullisia numerolaskuja) olisi havainto, että luku, jota halutaan jakaa tekijöihin, on välillä $(10^8,\,1{,}11\cdot 10^8)$, ja että neljän peräkkäisen luvun tulo päättyy muuhun kuin nollaan vain, jos viimeiset numerot ovat 1, 2, 3 ja 4 tai 6, 7, 8 ja 9. Koska jo 105²=(100+5)²>10⁴+10³ ja siis $105^4>(11\cdot 10^3)^2=1{,}21\cdot 10^8$, ainoiksi tekijäkandidaateiksi jäävät 101, 102, 103 ja 104.

42. Luku n! eli n-kertoma on tunnetusti lukujen $1, 2, 3, \dots, n$ tulo, esim. $4!=2\cdot 3\cdot 4=24$. Jos n on isohko, n! on kovasti suuri luku. Esim. $13!=6\,227\,020\,800$. Isompien lukujen kertomat näyttävät päättyvän useampiin nolliin. Kuinkahan moneen nollaan päättyy luku 1998!, jos se kirjoitettaisiin normaaliin tapaan auki? Perustele!

Immo Heikkisen ratkaisu. Luvun loppunollien määrä riippuu siitä, kuinka monta kymppiä saadaan muodostettua sen tekijöistä. Koska $10 = 2\cdot 5$, on loppunollien lukumäärä itse asiassa sama kuin luvun alkutekijähajotelman 2:n ja 5:n eksponenteista pienempi. Tarkastellaan luvun 1998! tekijöitä ja yritetään saada selville kuinka monta niistä on viitosia. Joka viides luvuista on jaollinen viidellä ja koska 1998/5 = 399,6, on 1998 tekijöistä 399 jaollisia viidellä. Mutta mutta. Näistä joka viides (79) on jaollinen 5²:lla. Näistä taas joka viides (15) on jaollinen 5³:lla. Ja edelleen joka viides (3) jaollinen 5⁴:lla. Ts. 5:n eksponentti alkutekijähajotelmassa on:

399 + 79 + 15 + 3 = 496,

joka onkin loppunollien lukumäärä koskapa kakkosia on "reilusti" enemmän. Siis luvussa 1998! on 496 loppunollaa.

43. Toinen omituinen kysymys loppunollista. Alkuluvut ovat jaottomia positiivisia kokonaislukuja; 1 ei yleisesti noudatettavan sopimuksen mukaan kuitenkaan ole alkuluku. Olkoot nyt p₁, p₂, ..., p₉₉, p₁₀₀ sata pienintä alkulukua. Muodostetaan luku

$$n=p_1^1\cdot (p_1^2p_2)(p_1^3p_2^2p_3)\cdots(p_1^{100}p_2^{99}p_3^{98}\cdots p_{98}^3p_{99}^2p_{100}^1).$$

Kuinkahan moneen nollaan n päättyy?

Immo Heikkisen ratkaisu. Tämä tehtävä menee samalla tavalla kuin edellinenkin, alkutekijähajotelman muodostaminen vain on helpompaa, koska tekijöinä on pelkästään alkulukuja. Olemme kiinnostuneita erityisesti alkulukujen p₁ = 2 ja p₃ = 5 eksponenteista.

$$n = p_1(p_1^2p_2)\cdots(p_1^{100}p_2^{99}\cdots p_{100}^1) =... ...ts p_{100}^1 = p_1^{5050}p_2^{4950}p_3^{4851}\cdots p_{100}^1.$$

Nyt koska 5:n eksponentti on 4851 ja koska 2:n eksponentti on suurempi, on luvussa loppunollia 4851 kpl.

44. Kuuluisa 1600-luvulla elänyt ranskalainen matemaatikko Pierre de Fermat esitti aikanaan muotoa 2²ⁿ+1olevia lukuja koskevan otaksuman (että ne olisivat kaikki alkulukuja), jonka yhtä kuuluisa 1700-luvulla elänyt sveitsiläinen Leonhard Euler osoitti virheelliseksi. Lukuja F_n=2²ⁿ+1 eli $5, 17, 257, 65537, \dots$ kutsutaan kuitenkin Fermat'n luvuiksi. Todista, että F_n (auki kirjoitettuna) päättyy aina numeroon 7, kun n>1.

Immo Heikkisen ratkaisu. Todistetaan täydellisellä induktiolla, että kaikille n>1 luvun F_n = 2²ⁿ + 1 viimeinen numero on 7. Kun n=2, on F₂ = 2²² + 1 = 17, joten väite pätee. Oletetaan, että väite pätee, kun n=k. Siis F_k=2^2k + 1 = 10m + 7 jollekin luvulle m eli 2^2k = 10m + 6. Kun n=k+1, on F_k+1 = 2^2k+1 + 1 2^(2k)2 + 1= (10m + 6)² + 1= 100m² + 120m + 36 + 1= 100m² + 120m + 30 + 7= 10(10m² + 12m + 3) + 7, eli F_k+1 päättyy 7:ään. Induktioperiaatteen nojalla väite on tosi.

45. Tehdään seuraavat havainnot: $1\cdot 2\cdot 3\cdot 4+1=25=5^2$, $2\cdot 3\cdot 4\cdot 5+1=121=11^2$, $3\cdot 4\cdot 5\cdot 6=361=19^2$. Onko seuraava väite aina tosi: jos kerrotaan keskenään mitkä tahansa neljä peräkkäistä kokonaislukua ja tulokseen lisätään yksi, tulokseksi saadaan neliöluku eli kokonaisluvun toinen potenssi?

Immo Heikkisen ratkaisu. Tutkitaan mielivaltaisen neljän peräkkäisen kokonaisluvun tulon ja 1:n summaa. Olkoon luvut n, n+1, n+2, n+3. Silloin n(n+1)(n+2)(n+3) + 1= n⁴ + 6n³ + 11n² + 6n + 1= n⁴ + 3n³ + n² + 3n³ + 9n² + 3n + n² + 3n + 1= n²(n² + 3n + 1) + 3n(n²+ 3n + 1) + n² + 3n + 1= (n² + 3n + 1)(n² + 3n + 1)= (n² + 3n + 1)², joka on kokonaisluvun neliö. Siis väite on tosi.

46. Tuntuu jo vähän omituiselta: jos otetaan mikä hyvänsä kolminumeroinen luku, kerrotaan se kahdella ja kirjoitetaan luvut peräkkäin kuusi- tai seitsennumeroiseksi luvuksi (se kaksinkertainen ensin), niin syntynyt luku on tasan jaollinen 23:lla ja 29:llä. Perustele tämä!

Immo Heikkisen ratkaisu. Olkoon tämä kolminumeroinen luku x. Kerrotaan se kahdella ja kirjoitetaan luvut peräkkäin (se kaksinkertainen ensin) eli: $1000\cdot 2x + x = 2001x$. Luku 2001 on jaollinen sekä 23:lla että 29:llä, joten tämä jaollisuus ei riipu millään tavalla x:stä.

Uudet tehtävät.

Tällä kertaa teemana ovat neliöjuuret. Tiesitkö, että $\sqrt {\phantom{0}}$-merkki on itse asiassa muotoiltu r-kirjain, latinan juurta tarkoittavan radix-sanan ensimmäinen kirjain? Sama radix esiintyy vaikkapa retiisissä tai radikaalissa.

47. Osoita, että luvun $(4+\sqrt {10})^n$ kokonaisosa on kaikilla n pariton luku.

48. Ratkaise yhtälö

$$\sqrt {3x^2-4x+34}+\sqrt {3x^2-4x- 11}=9.$$

49. Todista, että kaikilla $n\ge 0$ on olemassa m siten, että

$$(\sqrt 2+1)^2=\sqrt m-\sqrt {m-1}.$$

50. Ratkaise yhtälö

$$\sqrt{5-\sqrt {5+x}}=x.$$

51. Ratkaise yhtälö

$$\underbrace{\sqrt {x+2\sqrt {x+2\sqrt {x+\cdots+2\sqrt {x+2\sqrt {3x}}}}}}_{n\ {\rm juurimerkki\ddot a}}=x$$

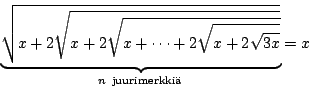
52. Osoita, että lukua $100+60\sqrt 3$ ei voi kirjoittaa muotoon $(x+y\sqrt 3)^2$ millään reaaliluvuilla x, y.

Lähetä ratkaisusi osoitteella Matti Lehtinen, Peukaloisentie 4 A 6, 00820 Helsinki, tai sähköpostilla osoitteeseen matti.lehtinen@helsinki.fi . Hyvät ratkaisut julkaistaan Solmussa. Myös jo käsiteltyihin tehtäviin voi lähettää uusia ratkaisuja!

Matti Lehtinen

Solmu 5/1998-1999
Viimeksi muutettu 23. marraskuuta 1999.