

Suojaus löydetään ratkaisemalla kahden tuntemattoman yhtälöryhmä. Saadulle ratkaisulle esitetään lopuksi todennäköisyystulkinta.
Tarkastellaan seuraavaa esimerkkiä, jossa telakka saa vuoden 1999 alussa tilauksen laivasta, joka maksetaan sen valmistuttua vuoden 2001 alussa. Kaupan hinnaksi sovitaan miljardi dollaria.
Oletetaan, että dollarin ja markan välinen kurssi vuoden 1999 alussa on viisi markkaa ja kaupan hinta on laskettu tällä kurssilla. Sopimuksen perusteella telakka saa maksun vasta vuoden 2001 alussa, jolloin dollarin kurssi voi olla joko noussut tai laskenut. Etenkin, jos kurssi laskee, niin telakka voi joutua vaikeuksiin, koska se on laskenut voivansa käyttää tilauksen valmistamiseen viisi miljardia markkaa.
Voiko dollarin kurssin heilahteluihin varautua etukäteen? Jatkossa näytetään, että tämä on mahdollista ja lasketaan, mitä tämä riskiltä suojautuminen maksaa.
Jokainen henkilö voi jakaa varallisuutensa V kahteen osaan: osakkeisiin ja talletuksiin. Osake on itse asiassa yleisnimi, jolla tarkoitetaan finanssimatematiikassa tavallista osaketta, valuuttakurssia, raaka-aineiden hintaa; ylipäätään mitä tahansa sellaista, mitä voidaan ostaa ja myydä ja minkä hinta huomenna on tuntematon. Talletuskin on yleisnimi, millä puolestaan tarkoitetaan kaikkea sellaista, minkä arvo huomenna voidaan laskea, kun tunnetaan sen arvo tänään. Esimerkkejä talletuksesta ovat pankkitalletukset ja obligaatiot.
Tarkastellaan yhden askeleen mallia, missä on ainostaan kaksi erilaista ajankohtaa: nykyisyys ja huominen; merkitään aikaa indeksillä t, joka siis saa vain kaksi arvoa t = 0 (nykyisyys) ja t = 1(huominen).
Talletusta merkitään kirjaimella B ja osaketta kirjaimella S. Varallisuutta V, osaketta S ja talletusta Btarkastellaan ajan funktiona -- tällöin merkitään V0, kun tarkoitetaan varallisuutta tänään, S1 kun tarkoitetaan osakkeen hintaa huomenna jne. Talletuksen arvo tänään on B0 = 1.
Alkupääomaksi sanotaan varallisuutta V0.
Päivän aikana päätetään talletuksen määrä ja osakkeiden
määrä, mutta alkupääomaa ei enää muuteta:
yhtälöiden avulla kirjoitettuna siis
V0 = ![]() B0 +
B0 + ![]() S0.Pari
S0.Pari
![]() ,
,![]() on strategia:
finanssimatematiikassa tutkitaankin sitä, kuinka tämä pari pitäisi valita.
Vakio
on strategia:
finanssimatematiikassa tutkitaankin sitä, kuinka tämä pari pitäisi valita.
Vakio ![]() kertoo talletuksen määrän ja
kertoo talletuksen määrän ja ![]() puolestaan
kertoo osakkeiden määrän.
Varallisuus huomenna voidaan nyt kirjoittaa yhtälönä
puolestaan
kertoo osakkeiden määrän.
Varallisuus huomenna voidaan nyt kirjoittaa yhtälönä
Osakkeen hinta St voi huomenna olla joko laskenut, S1 = (1 + a)S0, tai noussut S1 = (1 + y)S0. Tuntematonta on siis huominen arvo, tunnettua puolestaan on se, että osakkeen arvo on joko (1 + a)S0 tai (1 + y)S0. Talletuksen "hinta" taas kasvaa kiinteätä korkoa ja sen arvo huomenna on B1 = (1 + r)B0, jos sen arvo tänään on B0. Kun korko r tunnetaan, tiedetään myös talletuksen arvo huomenna. Talletus voi olla myös negatiivinen -- velasta siis maksetaan samaa korkoa kuin pankissa olevasta rahastakin.
Markkinoilla tehdään sopimuksia osakkeeseen liittyen. Esimerkkinä tarkastellaan eurooppalaista osto-optiota, missä sopimuksen ostajalla on oikeus ostaa osake huomenna tiettyyn kiinteään hintaan K. Sopimuksen myyjä puolestaan on velvollinen myymään osakkeen hintaan K. Myyjän kannalta tilanne on seuraava:
Kaavana myyjän tappio tai vaade on
f (S1) ![]() max(S1 - K, 0).
Mikä on option
arvo tänään? Tunnettuja ovat osakkeen hinta S0, lyhyt korko r ja
osakkeen mahdolliset arvot huomenna.
max(S1 - K, 0).
Mikä on option
arvo tänään? Tunnettuja ovat osakkeen hinta S0, lyhyt korko r ja
osakkeen mahdolliset arvot huomenna.
Osakkeen arvon kasvusta, lyhyestä korosta rja toimeenpanohinnasta K oletetaan
Eurooppalaisen osto-option arvo määrätään hakemalla ns.
suojaus.
Haetaan strategia
(![]() ,
,![]() ) siten, että
varallisuus huomenna on yhtä suuri kuin mahdollinen tappio:
) siten, että
varallisuus huomenna on yhtä suuri kuin mahdollinen tappio:
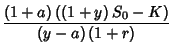 ja
ja 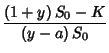 .
.
Tarkastellaan tähän tulokseen liittyviä oletuksia. Oletus (2) on melko luonnollinen. Jos r < a < y, niin osakkeen hinta kasvaisi aina talletusta nopeammin, ja tällöin kannattasi ottaa pankista vaikka sata miljoonaa velkaa, sijoittaa ne kaikki osakkeeseen ja myydä osakkeet huomenna ja varma voitto olisi vähintään 108(a - r) markkaa. Jos taas K < S0(1 + a), niin osto-option myyjän tulisi aina varautua tappioon -- tosin hinta voidaan kyllä tässäkin tapauksessa optiolle määrätä.
Oletus siitä, että osakkeen hinta voi huomenna saada kaksi eri arvoa on puolestaan aivan oleellinen yllä esitetylle suojauksen konstruoinnille. Siitä seuraa, että kaikki sopimukset ovat suojattavissa -- tällöin sanotaan että markkinamalli on täydellinen. Mikäli hinta voisi muuttua kolmeen eri arvoon, niin yhtälöryhmällä (3) ei enää ole yksikäsitteistä ratkaisua ja suojausta ei enää voi konstruoida. Saadaan esimerkki epätäydellisestä markkinamallista, missä tasapuolista hintaa ei ole. Erilaiset epätäydelliset markkinamallit ovat tällä hetkellä finanssimatematiikan keskeisiä tutkimuskohteita.
Lasketaan kaavan (4) perusteella suojaussopimuksen hinta yhdelle dollarille. Ratkaistaan ensin vakiot y ja a: (1 + y)5 = 5, 20 mistä vakion y arvoksi saadaan 0, 04 ja vakion a arvoksi vastaavasti -0, 04. Korko r on = 0, 02. Tarkastelujakso on siis kaksi vuotta. Kaavasta (4) saadaan nyt sopimuksen hinnaksi
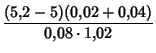 =
= Verrataan tilannetta siihen, että suojausta ei tehdä: jos dollarin hinta nousee, saadaan voittoa 200.000.000 markkaa, jos putoaa, niin tappiota tulee saman verran. Jos suojaus tehdään, niin voittoa tulee noin 53.000.000 markkaa ja tappiota tulee sopimuksen hinnan verran eli noin 147.000.000 markkaa. Etuna on tietenkin se, että kahden vuoden kuluttua ei enää ole mitään riskiä ja telakka voi suunnitella toimintaansa varmana siitä, että dollarin kurssin heilahtelu ei aiheuta uusia lisäkuluja.
Olkoon ![]() satunnaismuuttuja, joka saa arvon y todennäköisyydellä
p, ja arvon a todennäköisyydellä 1 - p ja Y satunnaismuuttuja, joka
saa arvon 1, jos
satunnaismuuttuja, joka saa arvon y todennäköisyydellä
p, ja arvon a todennäköisyydellä 1 - p ja Y satunnaismuuttuja, joka
saa arvon 1, jos ![]() = y ja arvon 0, jos
= y ja arvon 0, jos ![]() = a. Tällöin
= a. Tällöin
Osoitetaan lopuksi, että option myyjän diskontattu tappio huomenna on sama kuin käsiteltävän option tasapuolinen hinta:
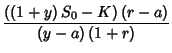 .
.
Yllä käsitelty markkinamalli on monessa mielessä epärealistinen. Yleensä osakekauppaan liittyy sivukuluja: kaupan välittäjä ottaa yleensä palkkion. Edelleen pankkitalletuksen korko on pienempi kuin velan korko. Lainsäädäntökin saattaa olla esteenä: osakkeiden lyhytmyynti oli Suomessa kiellettyä vielä kymmenen vuotta sitten. Kuitenkin yllä kuvatun yhden askeleen mallin yleistystä useamman askeleen malliksi, ns. binomipuuta, käytetään melko yleisesti erilaisten optioiden hinnoitteluun.
Johdannon tähän kiehtovaan ongelmakenttään löytää Stanley R. Pliskan kirjasta Introduction to Mathematical Finance -- Discrete time models, Blackwell 1997.
Esko Valkeila