Solmun tehtävät

Solmun tehtävät 36 - 40 esitettiin Solmussa 3/97-98. Tässä ratkaisut. Havaitset, että monissa tehtävissä ajatusta selvittää, jos esittää "vierasta" vaikkapa pisteellä tai pikku ympyrällä ja "kättelyparia" pisteet tai ympyrät yhdistävällä viivalla. Tehtävissä on oikeastaan kysymys verkoksi kutsutusta matemaattisesta rakenteesta, jota sovelletaan monenlaisiin asioiden ja esineiden välisiä konkreettisia tai abstrakteja yhteyksiä sisältäviin tilanteisiin.

Vanhojen tehtävien ratkaisuja

36. Kutsuilla on 35 vierasta ja isäntä. Kaikki paikalla olijat kättelevät toisensa. Montako kättelyä kutsuilla tapahtuu? Johda lauseke, joka kertoo kättelyjen määrän, kun kättelijöitä on n kappaletta.

1. ratkaisu. Isäntä kättelee kaikki 35 vierasta. Ensimmäinen vieras kättelee isännän lisäksi kaikki myöhemmin tulleet 34 vierasta. Toinen vieras kättelee isännän ja ensiksi tulleen vieraan lisäksi kaikki 33 myöhemmin tulevaa vierasta jne. Kättelyjä on näin ollen 35 + 34 + 33 + ^... + 2 + 1 kappaletta. Yhteenlaskun tulos on 630, minkä saa joko laskemalla kaikki luvut yhteen tai huomaamalla, että summa voidaan purkaa muotoon 18 ^. 35 (18 paria 0 + 35, 1 + 34, ..., 17 + 18) tai käyttämällä 35:n ensimmäisen kokonaisluvun summan kaavaa ${\displaystyle{35\cdot 36\over2}}$.

2. ratkaisu. Jokainen kättelevä pari voidaan tulkita 36-alkioisen joukon 2-alkioiseksi osajoukoksi. Koska kaikki kättelevät kaikkia, kättelyjen määrä on sama kuin 36-alkioisen joukon 2- alkioisten osajoukkojen lukumäärä. Tätä lukumäärää merkitään matematiikassa symbolilla ${\displaystyle{36\choose2}}$, ja se on laskettuna ${\displaystyle{36\cdot 35\over1\cdot 2}}$ = 630.

Yleinen tapaus. Jos kättelijöitä on n kappaletta, kättelyjä on (n - 1) + (n - 2) + ...2 + 1 = 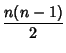${\displaystyle{n(n-1)\over2}}$ eli ${\displaystyle{n\choose2}}$ kappaletta. -- Yleisestihän pätee, että n-alkioisen joukon kaikkien k-alkioisten osajoukkojen lukumäärä on ${\displaystyle{n\choose k}}={\displaystyle{n(n-1)\cdots(n-k+1)\over k\cdot (k- 1)\cdots 2\cdot 1}}$.

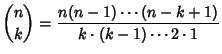37. Kutsuilla on paljon vieraita. Kukin vieras kättelee jotakin muita vieraita tai sitten ei kättele ketään. Osoita, että sellaisten vieraiden lukumäärä, jotka kättelevät parittoman määrän muita vieraita, on parillinen.

Ratkaisu. Olkoot vieraat V₁, V₂, ..., V_k ja vieraan V_j kättelemien vieraiden lukumäärä a_k. Merkitään kaikkien kättelytapahtumien lukumäärää n:llä. Silloin

a₁ + a₂ + ... + a_k = 2n,

sillä jokainen V_j:n tekemä kättely on samalla jonkin toisen vieraan V_i kättely ja sisältyy siis myös lukuun a_i. Koska lukujen a_j summa on parillinen, siinä ei voi olla paritonta määrää parittomia yhteenlaskettavia.

38. Kutsuilla on paljon vieraita. Jokainen vieras tuntee joitakin muista vieraista. Todista, että kutsuilla on ainakin kaksi vierasta, jotka tuntevat muista vieraista tasan yhtä monta. Tunteminen on molemminpuolista: jos A tuntee B:n, niin B tuntee A:n.

Ratkaisu. Olkoot vieraat taas V₁, V₂, ..., V_k ja olkoon vieraan V_j tuntemien toisten vieraiden lukumäärä b_j. Nyt b_j on aina luku, joka on $\ge$ 0 ja $\le$k - 1. Ajatellaan, että kutsuilla on joku, joka ei tunne ketään muuta vierasta. Koska tunteminen on molemminpuolista, ei yksikään vieras voi tuntea k - 1:tä muuta vierasta. Silloin jokainen luku b_j on ainakin 0, mutta enintään k - 2. Tämä merkitsee, että luvuilla b_j on enintään k - 1 eri mahdollista arvoa. Koska lukuja kuitenkin on k kappaletta, täytyy joidenkin kahden arvon olla samoja. Toinen mahdollisuus on, että kutsuilla jokainen vieras tuntee ainakin yhden toisen vieraan. Silloin jokainen b_jon ainakin 1. Nytkin lukujen b_j mahdollisia arvoja on enintään k - 1kappaletta (1, 2, ..., k - 1), mutta itse lukuja on k kappaletta. Jotkin kaksi b_j:tä ovat samat. Kummassakin tapauksessa ainakin kahdella vieraalla on yhtä monta tuttavaa. -- Tässä käytettiin laatikkoperiaatetta: jos n + 1 esinettä pitää sijoittaa n:ään laatikkoon, sijoittelua ei voi tehdä niin, ettei johonkin laatikkoon tulisi enemmän kuin yksi esine. Laatikkoperiaate on näennäisestä yksinkertaisuudestaan huolimatta tärkeä apuväline monissa matematiikan todistuksissa. Mieti tätä: voitko varmasti sanoa, että Suomessa on (ei kaljuja) ihmisiä, joilla on tasan yhtä monta hiusta päässään?

39. Kutsuilla on kuusi vierasta. Osa näistä on ehkä kätellyt toisensa, osa ei. Osoita, että vieraissa on välttämättä joko kolme sellaista jotka kaikki ovat kätelleet toisensa tai kolme sellaista, joista kukaan ei ole kätellyt muita kahta. Päteekö väite, jos puhutaan vain viidestä vieraasta?

Ratkaisu. Olkoot vieraat V₁, V₂, ..., V₆. Poimitaan V₁ erilleen. Loput viisi vierasta jakautuvat kahteen ryhmään sen mukaan, tuntevatko he V₁:n vai ei. Näistä ryhmistä toisessa on ainakin kolme jäsentä. Oletetaan ensin, että V₂, V₃ ja V₄kaikki tuntevat V₁:n. Jos näistä kolmesta jotkin kaksi tuntevat toisensa, he muodostavat V₁:n kanssa kolmikon, jonka kaikki jäsenet tuntevat toisensa. Jos näistä kolmesta mitkään kaksi eivät tunne toisiaan, on koossa kolmikko, jonka kaikki jäsenet ovat toisilleen outoja. Toinen mahdollinen tilanne on käsitellyn peilikuva. Jos V₂, V₃ ja V₄ ovat kaikki sellaisia, että he eivät tunne V₁:tä, niin joko jotkin kaksi tästä kolmikosta ovat myös toisilleen outoja ja muodostavat V₁:n kanssa outojen kolmikon, tai sitten kaikki kolme tuntevat toisensa, ja muodostavat siis tuttujen kolmikon.

Jos vieraita olisi vain viisi, V₁, V₂, V₃, V₄ ja V₅, voisi vallita esim. seuraava tilanne: V₁ tuntee V₂:n ja V₃:n, V₂tuntee V₅:n, V₃ tuntee V₄:n ja V₄ tuntee V₅:n. Nyt minkä hyvänsä kolmen vieraan joukossa on sekä sellaisia, jotka tuntevat toisensa, että sellaisia, jotka eivät tunne toisiaan. Tästä voi vakuuttua vaikkapa piirtämällä viisikulmion, jonka kärjet edustavat vieraita, ja siihen kaikki sivut ja lävistäjät niin, että jos V_ituntee V_j:n, jana V_iV_j on sininen ja jos V_i ei tunne V_j:tä, jana V_iV_j on punainen. Kuviossa ei ole yhtään kolmiota, jonka kaikki sivut olisivat samanväriset.

40. Kutsuilla on 17 vierasta. Osa on kätellyt toisensa, osa nyökännyt tervehdyksen toisilleen ja osa ollut kokonaan tervehtimättä. Osoita, että kutsuilla on jotkin kolme vierasta jotka joko kaikki ovat kätelleet, kaikki nyökänneet toisilleen tai kaikki jättäneet tervehtimättä toisensa.

Ratkaisu. Otetaan taas yksi vieras, sanokaamme V₁, erilleen. Loput 16 vierasta jakautuvat kolmeen joukkoon sen mukaan, miten he ovat tervehtineet V₁:n: kätelleet, nyökänneet ja tervehtimättömät. Jos kussakin ryhmässä olisi enintään viisi vierasta, heistä ei saataisi kokoon 16:ta. Ainakin jossain ryhmässä on siis ainakin 6 vierasta. Voimme olettaa, että kuusi vierasta V₂, V₃, ..., V₇ on kätellyt V₁:n. Jos jotkin kaksi näistä kuudesta, esim. V₂ ja V₃, ovat kätellet toisensa, niin V₁, V₂ V₃ on kolmikko, jonka kaikki jäsenet ovat kätelleet toisensa. Voi tietysti olla niinkin, että mitkään kaksi näistä kuudesta vieraasta eivät ole kätelleet. Mutta silloin meillä on kuuden vieraan joukko, jonka kaikki jäsenet ovat joko nyökänneet tai olleet tervehtimättä. Edellisen tehtävän mukaan tällaisessa tilanteessa löytyy aina joko kolmikko, jonka kaikki jäsenet ovat nyökänneet toisilleen, tai kolmikko, jonka kaikki jäsenet ovat olleet tervehtimättä. -- Tämä tehtävä on esitetty mm. 6. kansainvälisissä matematiikkaolympialaisissa vuonna 1964.

Uudet tehtävät

Tällä kertaa tehtävissä käsitellään yksinkertaisia asioita, nimittäin kokonaislukuja ja niiden kymmenjärjestelmäesitystä eli sitä, miltä ne näyttävät tavalliseen tapaan kirjoitettuina. Joihinkin ongelmiin saattaa löytyä yksinkertainen vastaus, jos ne syötetään matemaattiselle ohjelmistolle, kuten Mathematicalle tai Maplelle. Tarkoituksemme on kuitenkin päätyä vastauksiin päättelyn avulla, ehkäpä kynää ja paperia apuna käyttäen.

41. Luku 110 355 024 on neljän peräkkäisen positiivisen kokonaisluvun tulo. Mitkä nämä luvut ovat?

42. Luku n! eli n-kertoma on tunnetusti lukujen 1, 2, 3, ...n tulo, esim. 4! = 2 ^. 3 ^. 4 = 24. Jos n on isohko, n! on kovasti suuri luku. Esim. 13! = 6 227 020 800. Isompien lukujen kertomat näyttävät päättyvän useampiin nolliin. Kuinkahan moneen nollaan päättyy luku 1998!, jos se kirjoitettaisiin normaaliin tapaan auki? Perustele!

43. Toinen omituinen kysymys loppunollista. Alkuluvut ovat jaottomia positiivisia kokonaislukuja; 1 ei yleisesti noudatettavan sopimuksen mukaan kuitenkaan ole alkuluku. Olkoot nyt p₁, p₂, ..., p₉₉, p₁₀₀ 100 pienintä alkulukua. Muodostetaan luku

n = p₁^{1 .} (p₁²p₂)(p₁³p₂²p₃) ^... (p₁¹⁰⁰p₂⁹⁹p₃^{98 ...} p₉₈³p₉₉²p₁₀₀¹).

Kuinkahan moneen nollaan n päättyy?

44. Kuuluisa 1600-luvulla elänyt ranskalainen matemaatikko Pierre de Fermat esitti aikanaan muotoa 2²ⁿ + 1 olevia lukuja koskevan otaksuman (että ne olisivat kaikki alkulukuja), jonka yhtä kuuluisa 1700-luvulla elänyt sveitsiläinen Leonhard Euler osoitti virheelliseksi. Lukuja F_n = 2²ⁿ + 1 eli 5, 17, 257, 65537, ...kutsutaan kuitenkin Fermat'n luvuiksi. Todista, että F_n (auki kirjoitettuna) päättyy aina numeroon 7, kun n > 1.

45. Tehdään seuraavat havainnot: 1 ^. 2 ^. 3 ^. 4 + 1 = 25 = 5², 2 ^. 3 ^. 4 ^. 5 + 1 = 121 = 11², 3 ^. 4 ^. 5 ^. 6 = 361 = 19². Onko seuraava väite aina tosi: jos kerrotaan keskenään mitkä tahansa neljä peräkkäistä kokonaislukua ja tulokseen lisätään yksi, tulokseksi saadaan neliöluku eli kokonaisluvun toinen potenssi?

46. Tuntuu jo vähän omituiselta: jos otetaan mikä hyvänsä kolminumeroinen luku, kerrotaan se kahdella ja kirjoitetaan luvut peräkkäin kuusi- tai seitsennumeroiseksi luvuksi (se kaksinkertainen ensin), niin syntynyt luku on tasan jaollinen 23:lla ja 29:llä. Perustele tämä!

Jos haluat ratkaisujasi johonkin myöhempään Solmuun, lähetä niitä osoitteella Matti Lehtinen, Peukaloisentie 4 A 6, 00820 Helsinki, tai sähköpostilla matti.lehtinen@helsinki.fi.

Matti Lehtinen

Solmu 2/1998-1999
Last modified: Sun Jan 24 22:01:58 EET 1999