

Tapoja ellipsin piirtämiseen on paljon. Kiinnostunut lukija voi etsiä deskriptiivisen geometrian oppikirjoja; näistä löytyy yleensä monia tapoja ellipsin piirtämiseen.
Laskemista ja algebraa korostavana aikana -- kuten nyt -- lienee helpointa laskea ellipsin yhtälöön x2/a2 + y2/b2 = 1 perustuen riittävän monta pistettä ellipsin kehältä ja yhdistää nämä vapaalla kädellä.
Geometrisempiakin tapoja kuitenkin on. Menneinä vuosisatoina näitä olisi arvostettu nykyistä enemmän. Niillä on edelleenkin merkityksensä: puhtaan geometrisiin argumentteihin vetoaminen usein paljastaa tilanteesta piirteitä, jotka peittyvät raakaa algebraa käytettäessä.
Seuraavassa kaksi tapaa piirtää ellipsi. Toisessa konstruoidaan geometrisesti ellipsin pisteitä, toisessa sen tangentteja.
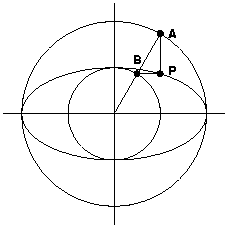
Piirretään aluksi samankeskiset ympyrät, joiden säteet ovat ellipsin puoliakselit a ja b. Ympyröiden yhteisestä keskipisteestä piirretään säde, joka leikatkoon ympyrät pisteissä A ja B. Piste P olkoon pisteen A kautta kulkevan pystysuoran ja pisteen B kautta kulkevan vaakasuoran leikkauspiste. Tällöin P on ellipsin piste. Piirtämällä useita säteitä ja etsimällä näitä vastaavat pisteet P saadaan lisää ellipsin pisteitä. Itse ellipsi piirretään vapaalla kädellä näiden kautta.
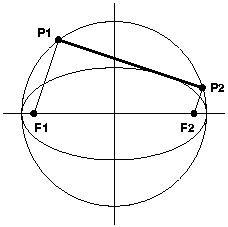
Toisessa tavassa lähtökohtana on edellä mainittu a-säteinen ympyrä ja tämän halkaisijalla olevat ellipsin polttopisteet F1 ja F2. Piirretään jokin polttopisteestä F1 alkava säde; tämä leikatkoon ympyrän pisteessä P1. Samansuuntainen pisteestä F2 alkava säde leikatkoon ympyrän pisteessä P2. Tällöin suora P1P2 on ellipsin tangentti. Muuttamalla säteiden suuntaa ja konstruoimalla eri suuntia vastaavat suorat P1P2 saadaan niin monta ellipsin tangenttia kuin halutaan. Ellipsi on tangenttien muodostaman suoraparven verhokäyrä ja se voidaan piirtää vapaalla kädellä.
Miten sitten voidaan osoittaa, että esitetyt konstruktiot todella antavat ellipsin pisteitä ja tangentteja? Ajatuksellisesti suoraviivainen tapa on käyttää analyyttista geometriaa. Edellinen konstruktio on varsin helppo laskea, jälkimmäinen on hieman työläämpi. Sen laskeminen on hyvä harjoitustehtävä symbolisten tietokoneohjelmien -- kuten Mathematica tai Maple -- käyttäjälle.
Myös puhtaasti geometriseen päättelyyn perustuvat todistukset ovat mahdollisia. Ne edellyttävät kuitenkin tottuneisuutta geometriseen ajatteluun, mikä tekee ne vaikeiksi: matematiikan opinnot antavat nykyään varsin heikot geometriset valmiudet.
Geometriset tarkastelut antavat kuitenkin kiintoisia sivutuloksia. Esimerkiksi polttopisteistä tangentin sivuamispisteeseen piirretyt säteet -- ellipsin polttosäteet -- muodostavat yhtä suuret kulmat tangentin kanssa. Tämä on ellipsin polttopisteominaisuus: Jos toisessa polttopisteessä on valolähde ja valonsäteet heijastuvat ellipsin kehästä fysikaalisen heijastumislain mukaisesti, niin ne kohtaavat toisessa polttopisteessä.
Edellä kuvattuja ellipsin piirtokonstruktioita voi näppärästi havainnollistaa Cabri-Geometria -tietokoneohjelman animaatioilla. Konfiguraatioiden määrittelytiedostot Cabrin DOS-versiolle ovat myös saatavissa Solmun verkkoversiosta.
Simo K. Kivelä