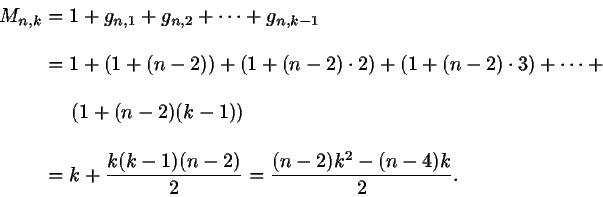Turistina matematiikassa

Lukujen museossa

A    Ensimmäinen kierros

Turistikohteemme on nyt museo. Yleisen mielikuvan mukaan antiikin kreikkalaisten matematiikka oli geometriaa. Museon kätköistä löytyy kuitenkin kreikkalaisten lukuteorian keksintöjä, joihin tietysti liittyy -- geometriaa. Aikaisemmista retkeilyistämme poiketen emme ota mukaan tehtäviä matkamuistoiksi, vaan matkaopas selittää kaikki kohteet kiertokäynnin aikana, osan, tähdellä merkityt kohteet, kuitenkin vasta retken lopussa.

Pythagoraan -- sen Pythagoraan lauseen Pythagoraan, joka eli 500 -luvulla eKr. -- mielestä kokonaisluvut olivat koko mailmankaikkeuden maagis-mystinen perusta. Pythagoraan oppilaat ja seuraajat ryhtyivät kiinnittämään huomiota lukuihin sinänsä. Luvut eivät olleet heille vain arkielämän laskennon välineitä. Näin syntyi perusta sille matematiikan haaralle, jota kutsutaan lukuteoriaksi.

Luvut voitiin lajitella eri tavoin: oli parillisia ja parittomia, parittoman parittomia (kuten 15 = 3$\cdot$5), parillisen parittomia (kuten 10 = 2$\cdot$5) ja parillisen parillisia (kuten 8 = 2$\cdot$4), alkulukuja ja yhdistettyjä lukuja, ystävällisiä lukuja, täydellisiä lukuja jne. Varmaan mielenkiintoisin luokittelu on alkuluku -- yhdistetty luku. Tällä kertaa ihmettelemme kuitenkin erästä Pythagoraan oppisuunnan keksintöä, monikulmiolukuja.

1. Yksinkertaisimpia monikulmiolukuja ovat kolmioluvut T_k:

$\bullet$	$\begin{matrix}\bullet\\ \bullet&\bullet\end{matrix}$	$\begin{matrix}\bullet\\ \bullet&\bullet\\ \bullet&\bullet&\bullet\end{matrix}$	$\begin{matrix}\bullet\\ \bullet&\bullet\\ \bullet&\bullet&\bullet\\ \bullet&\bullet&\bullet & \bullet\end{matrix}$
T1 = 1	T2 = 3	T3 = 6	T4 = 10

ja neliöluvut Q_k:

$\bullet$	$\begin{matrix}\bullet&\bullet\\ \bullet&\bullet\end{matrix}$	$\begin{matrix}\bullet&\bullet&\bullet\\ \bullet&\bullet&\bullet\\ \bullet&\bullet&\bullet\end{matrix}$	$\begin{matrix}\bullet&\bullet&\bullet&\bullet\\ \bullet&\bullet&\bullet& \bull... ... \bullet& \bullet&\bullet&\bullet\\ \bullet&\bullet&\bullet&\bullet\end{matrix}$
Q1 = 1	Q2 = 4	Q3 = 9	Q4 = 16

ja viisikulmioluvut P_k:

$\bullet$	$\begin{xy} 0;<0.5cm,0cm>: a(0)*{\bullet}+ a(72)*{\bullet}+ a(144)*{\bullet}+ a(216)*{\bullet}+ a(288)*{\bullet} \end{xy}$	$\begin{xy} 0;<0.5cm,0cm>: a(0)*{\bullet}+ a(72)*{\bullet}+ a(144)*{\bullet}+ a... ...et}+a(144)*{\bullet}+ a(216)*{\bullet}+a(216)*{\bullet}+ a(288)+a(288) \end{xy}$	$\begin{xy} 0;<0.5cm,0cm>: a(0)*{\bullet}+ a(72)*{\bullet}+ a(144)*{\bullet}+ a... ...et}+ a(216)*{\bullet}+a(216)*{\bullet}+a(216)*{\bullet}+ a(288)+a(288) \end{xy}$
P1 = 1	P2 = 5	P3 = 12	P4 = 22

2^*. Mitkä olisivat neljä ensimmäistä kuusikulmiolukua, neljä ensimmäistä seitsenkulmiolukua ja neljä ensimmäistä kymmenkulmiolukua?

3. n-kulmiolukujen M_n,k yleinen induktiomääritelmä voisi olla seuraava: M_n,1 = 1, M_n,2 = n. M_n,2 havainnollistetaan kuperana n-kulmiona ja sen n:ään kärkeen sijoitettuina pisteinä. Oletamme, että M_n,k on määritelty ja havainnollistettu kuperan n-kulmion kärjissä, sivuilla ja sisällä olevina pisteinä niin, että n-kulmion joka sivulla kärjet mukaan luettuina on n pistettä. Valitaan tämän n-kulmion yksi kärki ja siihen liittyvät sivut. Jatketaan näitä sivuja $${1\over k+1}$$-osalla niiden pituudesta ja sijoitetaan jatkeiden päähän uudet pisteet. Täydennetään kuvio alkuperäisen kanssa yhdenmuotoiseksi n-kulmioksi, ja sijoitetaan uusille sivuille kullekin (kärjet mukaan lukien) k+1 pistettä. Uuden kuvion pisteiden lukumäärä on M_n,k+1.

4^*. Erotus g_n,k = M_n,k+1-M_n,k on n-kulmiolukujen k:s gnomon. Sen havainnollistavat pistekonstruktiossa ne pisteet, jotka kuvioon lisätään, kun siirrytään M_n,k:n kuvasta M_n,k+1:n kuvaan. Neliölukujen tapauksessa tämä kuvio on suoran kulman näköinen, esimerkiksi

$$\begin{matrix}\bullet&\bullet&\bullet&\bullet\\ &&&\bullet \\ &&&\bullet \\ &&&\bullet \end{matrix}$$

Nimitys gnomon tulee samanmuotoisesta yksinkertaisesta mittausvälineestä, jota antiikin tähtitieteilijät käyttivät. Yhtenäisyyden vuoksi sovimme, että nollas gnomon g_n,0 = 1. Mikä on kolmiolukujen T_k = M_3,k k:s gnomon? Mikä on neliölukujen Q_k = M_4,k k:s gnomon? Mikä on viisikulmiolukujen P_k = T_5,k k:s gnomon? Entä n-kulmiolukujen?

5^*. Miten voidaan kuviolukujen avulla ilmoittaa summa 1+2+...+k? Entä k:n ensimmäisen parittoman luvun summa?

6^*. Päättele oikeaksi kaava Q_k = T_k-1+T_k.

7^*. Luku, joka on muotoa k(k+1), on pitkänomainen. Millainen kuvio havainnollistaisi pitkänomaista lukua? Päättele, mitä on T_k käyttämällä hyväksi pitkänomaisia lukuja. Mikä on summan 1+2+...+k arvo?

8^*. Minkä kaavan saat, jos poistat neliöstä, jonka sivu on pariton, keskipisteen ja jaat jäljelle jäävän osan pitkänomaisia lukuja kuvaaviksi kuvioiksi?

9^*. k-jäseninen aritmeettinen jono on lukujen a, a+d, a+2d,..., a+(k-1)d muodostama jono. Mikä on näiden lukujen summa?

10^*. Olemme jo selvittäneet, mikä on T_k. Monikulmioluku on peräkkäisten gnomoniensa summa:

$$M_{n,k}=g_{n,0}+g_{n,1}+\cdots+g_{n,k}.$$

Käytä tätä tietoa hyväksesi ja laske P_k. Laske myös kaikilla n pätevä k:nnen n-kulmioluvun M_n,k lauseke n:n ja k:n avulla.

11. 1200-luvulla elänyt italialainen Leonardo Pisano eli Fibonacci, joka tunnetaan parhaiten matematiikassa tavan takaa esiintyvästä Fibonaccin jonosta 1, 1, 2, 3, 5, 8, 13, ..., käytti monikulmiolukuihin perustuvia tietoja mielenkiintoisen summan laskemiseksi. Näin Fibonacci: Ryhmitellään peräkkäiset parittomat luvut seuraavasti:

$$\begin{matrix}1\\ 3&5\\ 7&9&11\\ 13&15&17&19\\ 21&23&25&27&29\\ &&...\end{matrix}$$

Nyt k:nnella rivillä on k lukua, ja k:nnen rivin lukujen keskiarvo on k². Näin ollen n:n ensimmäisen rivin lukujen summa on 1$\cdot$1²+2$\cdot$2²+3$\cdot$3²+...+n$\cdot$n². Näillä riveillä on lukuja kaikkiaan 1+2+3+...+n = T_n = $${1\over 2}$$n(n+1) kappaletta. Mutta p:n ensimmäisen parittoman luvun summa on p². Kun nämä havainnot yhdistetään, saadaan

$$1^3+2^3+\cdots+n^3 = {n^2(n+1)^2\over 4}.$$

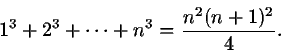
B Oppaan selitykset

2. Jos rupeaa sijoittelemaan kuusikulmioihin pisteitä samalla menetelmällä kuin viisikulmioihin, niin ensin on yksi, sitten kuusi, seuraavassa vaiheessa 15 ja neljännessä 28 pistettä. Kymmenkulmiolle piirtäminen tulee jo vaikeammaksi ja se vaatii huolellisuutta. Ensimmäiset kaksi 10-kulmiolukua ovat 1 ja 10, kolmas 27 ja neljäs 52.

4. Kolmiolukujen peräkkäiset gnomonit ovat 1, 2, 3, jne; k:s gnomon on k+1, neliöluvuille ensimmäiset gnomonit ovat 1, 3, 5 ja 7 (kuten kuvassa). Neliölukujen k:s gnomon on 2k+1. Viisikulmioluvuille ensimmäiset gnomonit ovat 1, 4 ja 7. Viisikulmiolukujen k:s gnomon sisältää 4 uutta viisikulmion kärkeä ja kunkin kolmen uuden sivun k-1 pistettä. Siis g_5,k = 4+3(k-1) = 1+3k. n-kulmiolukujen gnomonit g_n,0 = 1 ja g_n,1 = n-1 ovat ilmeisiä. g_n,k:n määrittämiseksi ajatellaan kohdassa 3 esitettyä konstruktiota. Kun M_n,k:n kuvaan lisätään pisteitä M_n,k+1:n saamiseksi, joudutaan sijoittamaan uusi piste uuden isomman n-kulmion kaikkiin muihin kärkiin paitsi yhteen. Tämä merkitsee n-1:tä uutta pistettä. Lisäksi joudutaan piirtämään n-2 uutta monikulmion sivua ja näihin pisteitä niin, että joka sivulle tulee kärjet mukaan lukien k+1 pistettä. Kun kärjet on jo miehitetty, uusia pisteitä on piirrettävä vielä (n-2)(k-1) kappaletta. Siis

$$\mbox{}g_{n,k} = n-1+(n-2)(k-1) = (n-2)k+1.$$

Tarkistuksen vuoksi voimme sijoittaa tähän kaavaan jo käsitellyt arvot k =0 ja k = 1 sekä n = 3, 4 ja 5. Se tuntuu toimivan!

5. Kuvioista voidaan päätellä heti, että

$$1+2+3+\cdots+k=T_k$$

ja

$$1+3+5+\cdots 2k+1=Q_k=k^2.$$

6. Jaa k $\times$ k-neliö kahdeksi suorakulmaiseksi kolmioksi, joista toisen pisin sivu on neliön lävistäjä. Kolmiot edustavat lukuja T_k ja T_k-1.

7. Tapauksessa n = 5 pitkänomaisen luvun 20 kuva olisi

$$\begin{matrix}\bullet&\bullet&\bullet&\bullet&\bullet\\ \bul... ...&\bullet\\ \bullet&\bullet&\bullet&\bullet&\bullet\end{matrix}$$

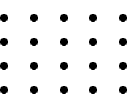
Kuvio voidaan jakaa kahdeksi yhteneväksi kolmioksi, jotka kumpikin edustavat kolmiolukua T₄ = 10. Yleisesti pitkänomainen luku k(k+1) voidaan jakaa kahdeksi T_k:ta edustavaksi kolmioksi. Mutta tämä merkitsee sitä, että 2T_k = k(k+1) ja T_k = $${1\over 2}$$k(k+1). Numeron 5 perusteella on siis

$$1+2+3+\cdots+k={k(k+1)\over 2}.$$

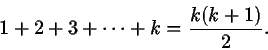
8. Olkoon neliön sivu 2k+1. Keskipisteen poiston jälkeen jää kuvio, joka voidaan jakaa neljäksi pitkänomaiseksi luvuksi. Mutta kukin tällainen on kahden kolmioluvun summa. Saadaan

$$\mbox{}8T_k+1=Q_{2k+1}=(2k+1)^2.$$

9. Summassa on k a:ta ja d:llä kerrottuna summa 1+2+3+...+k-1, joka numeron 7 mukaan on $${1\over 2}$$(k-1)k. Aritmeettisen jonon summa on siis

$$ka+{(k-1)kd\over 2}$$

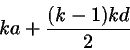
10. Viisikulmiolukujen gnomon on 1+3k. P_k on gnomoniensa summa:

$$P_k=1+(1+3)+(1+3\cdot 2)+\cdots+(1+3(k-1)).$$

Mutta tämä summa on aritmeettisen jonon summa. Voimme soveltaa edellisen numeron kaavaa, jossa nyt a = 1, d = 3. Siis P_k = k+ $${3\over 2}$$k(k- 1) = $${3\over 2}$$k²- $\dfrac{1}{2}$k. Yleiselle monikulmioluvulle saadaan samalla tavalla

$$\begin{split} M_{n,k}&=1+g_{n,1}+g_{n,2}+\cdots+g_{n,k-1}\\ \... ...=k+\frac{k(k-1)(n-2)}{2}=\frac{(n-2)k^2-(n-4)k}{2}. \end{split}$$

Matti Lehtinen
Matti.Lehtinen@Helsinki.FI
Solmu 3/1997-1998