Lumihiutaleesta

Fraktaalit ja kaaos ovat muodikkaita käsitteitä. Solmun numerot 1/97-98 ja 2/97-98:kin valitsivat kansikuvikseen von Kochin lumihiutalekäyrän ja erään Kleinin ryhmän rajajoukon osan. Yksi merkittävä syy fraktaalien suosioon on, että monet fraktaalit ovat hyvin symmetrisiä, ja samat muodot toistuvat niissä eri mittakaavoissa. Tämä fraktaalien kauneus on epäilemättä osaltaan lisännyt myös matemaatikoiden mielenkiintoa fraktaalien tutkimukseen.

Kun Mandelbrot otti käyttöön sanan fraktaali kuvaamaan "rikkonaisia ja jollain tavalla monimutkaisia joukkoja" 1970-luvun puolivälissä, hän korosti kirjassaan fraktaalien merkitystä luonnontieteissä ja luonnossa. Yksi Mandelbrotin argumenteistä on: Kun katsotaan riittävän tarkasti, huomataan, että luonnossa ei ole suoria viivoja. Esimerkiksi Britannian rantaviiva onkin äärettömän pitkä, likimain 1,5-ulotteinen käyrä! Myös pörssikurssien heilahtelun kuvaaja on "luonnon fraktaalikäyrä", sen dimension arvioidaan olevan noin 1,4, mitä sillä sitten tarkoitetaankaan... Tällaiset "sovellukset", joissa esiintyy mystisiä kokonaisluvuista poikkeavia dimensioita, takaavat omalta osaltaan fraktaalien kansansuosion jatkossakin. Toisaalta joku voisi esittää vastaväitteen, ettei luonnossa ole "oikeita matemaattisia fraktaaleja", mitä ne sitten ovatkaan. Mitä fraktaalit sitten oikeasti ovat? Valitettavasti kysymykseen on vaikea antaa kattavaa vastausta, enkä yritä sellaista tässäkään antaa. Kuitenkin tarkastelemalla esimerkkinä von Kochin vuonna 1904 esittämää lumihiutalekäyrää, on (ehkä) mahdollista saada käsitys jo mainitusta fraktaalidimension käsitteestä. Ainakin sellaista joukkoa, jonka fraktaalidimensio ei ole kokonaisluku, voi rauhallisin mielin kutsua fraktaaliksi.

Katsotaan yksinkertaisuuden vuoksi vain lumihiutaleen kolmasosaa. Se saadaan kuvan 1 prosessilla:

1.

Aloitetaan yksikköjanasta (Kuva 1a).

2.

Jaetaan jana kolmeen yhtä pitkään palaan, heitetään keskimmäinen pois, ja korvataan se kahdella samanmittaisella janalla, jotka muodostavat alkuperäisen janan kahden jäljellä olevan palan kanssa yhtenäisen murtoviivan (Kuva 1b).

3.

Toistetaan kohta (2) jokaiselle kuvioon sisältyvälle janalle, jonka pituus on kolmasosa edellisen vaiheen janojen pituudesta.

Kun tätä prosessia toistetaan, tuloksena saatava käyrä lähestyy "todellista von Kochin lumihiutaletta".

Kuva 1: Lumihiutaleen kolmanneksen kehitysvaiheita

Lumihiutaleen piirtäminen siis aloitetaan janasta, joka on selvästi 1-ulotteinen. Samoin, jos toistamme edellä kuvailemaani piirtoprosessia kuinka monta kertaa tahansa, välituloksena saatavan murtoviivan pituus on aina äärellinen, itse asiassa, jos vaihe (2) toistetaan n kertaa, tuloksena on murtoviiva, jonka pituus on 4ⁿ/3ⁿ. (Murtoviiva koostuu 4ⁿ palasta, joista kukin on pituudeltaan (1/3)ⁿ.) Samoin, jos katsomme käyrää tarpeeksi suurella suurennuslasilla, se näyttää melkein jokaisessa pisteessä janalta. Kyseessä on siis selvästi 1-ulotteinen käyrä. Kuitenkin käyrän pituus lähestyy ääretöntä, kun n kasvaa. Samalla laskulla huomaamme, että "mielivaltaisen lyhytkin" pätkä lumihiutalekäyrää on äärettömän pitkä! Lumihiutaleessa on siis jotain outoa. Mandelbrotin mukaan esimerkiksi Bretagnen, tai yhtä hyvin Suomen rantaviivan pituuden mittaaminen tarkemmalla ja tarkemmalla mittakaavalla antaisi vastaavanlaisen tuloksen... Jos lumihiutalekäyrä ei ole 1-ulotteinen, onko se sitten 2-ulotteinen? Esimerkiksi yksikköneliö on hyvä kaksiulotteinen "mallikappale". Jos kappale on 2-ulotteinen, sillä voisi ajatella olevan nollaa suurempi pinta-ala, kuten neliöllä, ja ympyrän tai vaikkapa kokonaisen lumihiutalekäyrän rajoittamalla tasoalueella. (Osaatko laskea lumihiutaleen rajoittaman pinta-alan?) Lasketaan siis lumihiutalekäyrän pinta-ala: Ensimmäinen havainto on, että (ilmeisesti) lumihiutalekäyrän kolmasosa mahtuu kokonaan yksikköneliön sisään (Kuva 2a). Siis käyrän pinta-ala on pienempi kuin 1. Toisaalta käyrä koostuu neljästä pienennetystä omasta kopiostaan, joten käyrän voi peittää myös neljällä 1/3-sivuisella neliöllä, jotka on aseteltu kuten kuvassa 2b. Siis pinta-ala on alle 4$\cdot$(1/3)² = (2/3)² = 4/9. Lisäämällä neliöiden määrää ja vastaavasti pienentämällä niiden sivujen pituutta, huomaamme, että käyrän pinta-ala on pienempi kuin (2/3)²ⁿ millä tahansa luonnollisella luvulla n. (Lumihiutalekäyrä peittyy 4ⁿ = 2²ⁿ neliöllä, joiden sivut ovat pituudeltaan (1/3)ⁿ, siis pikkuneliöillä, joiden pinta-ala on ((1/3)ⁿ)² = (1/3)²ⁿ.) Näiden peitteiden pinta-ala (2/3)ⁿ lähestyy nollaa, kun n kasvaa, joten lumihiutalekäyrän pinta-ala vaikuttaisi olevan 0, mikä ei ole kaksiulotteisuuden kannalta kovin lupaavaa.

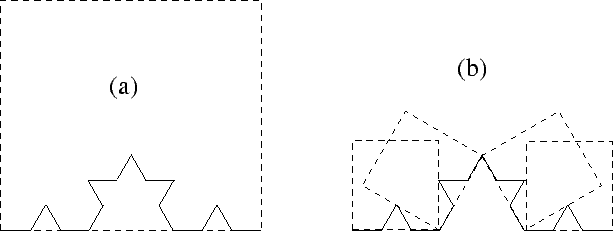
Kuva 2: Mikä on lumihiutaleen pinta-ala?

Tarkastellaanpa edellä tehtyjä laskuja uudelleen: Ensin laskimme yhteen sivunpituuksia, siis lukuja (1/3) ${}^{1\cdot n}$ ja saimme tulokseksi äärettömän. Sitten laskimme yhteen pinta-aloja, siis lukuja (1/3) ${}^{2\cdot n}$ ja saimme tulokseksi nollan. Näissä lausekkeissa esiintyvä sivunpituuden (1/3)ⁿ eksponentti on siis ilmeisesti dimensio; jos ensimmäinen summa olisi ollut äärellinen, olisimme todenneet käyrän 1-ulotteiseksi, jos taas jälkimmäinen summa olisi lähestynyt positiivista raja-arvoa, olisimme arvelleet sitä kaksiulotteiseksi. Klassisen geometrian mielessä olemme siis löytäneet erikoisen väliinputoajakäyrän. Yleistämällä tästä pääsemme esimerkiksi seuraavanlaiseen ajatukseen: Jos on olemassa eksponentti 1<$\delta$<2, jolle termien (1/3) ${}^{\delta\cdot n}$ summat 4ⁿ(1/3) ${}^{\delta n}$ lähestyvät positiivista ja äärellistä raja-arvoa, $\delta$ on lumihiutalekäyrän "fraktaalidimensio". Lumihiutaleen tapauksessa tällaisen $\delta$:n löytäminen on kohtuullisen helppoa: Jonolla 4ⁿ(1/3) ${}^{\delta n}$ on äärellinen, positiivinen raja-arvo täsmälleen silloin, kun $\delta$ = log₃ 4. Tällöin nimittäin logaritmin ominaisuuksista seuraa:

$$4^n(1/3)^{\delta n}=4^n(3^\delta)^{-n} = 4^n4^{-n} =1\to 1, \quad\text{kun}\quad n\to\infty.$$

Vaikuttaisi siis siltä, että olemme päätyneet (ehkä hieman vapaamielisellä päättelyllä) tulokseen: Kochin lumihiutalekäyrä on fraktaali, ja sen fraktaalidimensio on log₃ 4 =ln 4 / ln 3$\approx$ 1,26. Tarkkaavainen lukija varmaankin huomasi, ettemme edellä edes määritelleet "fraktaalidimension" käsitettä vaikka puhuimmekin siitä luontevasti... Muutenkin päättely oli paikoin vauhdikasta. Tarkoitukseni olikin antaa vain jonkinlainen tuntuma dimensiokäsitteeseen käsittelemällä sopivaa esimerkkiä; aiheen perusteellinen ja vedenpitävä käsittely vaatisi melko lailla enemmän valmistelua. Kiinnostuneet lukijat voivat koettaa saada käsiinsä esimerkiksi lähdeluettelossa mainitun Devaneyn kirjan, jossa aihetta käsitellään hieman enemmän, mutta kuitenkin tasolla, joka on lukiolaisen tiedoilla saavutettavissa. Lopussa listatuista www-osoitteista löytyvien linkkien avulla on myös mahdollista löytää tietoa (ja huuhaata...). Vakavampaa ja vaativampaa lukemista kaipaavalle voi suositella Falconeria.

Lukemista

P. Mattila: Fraktaalien suosion syitä, Arkhimedes 3/89, sivut 159-164. B. Mandelbrot: The fractal geometry of nature, Freeman, 1977/1982.

R. Devaney: Chaos, fractals and dynamics: Computer experiments in mathematics,
Addison Wesley, 1991.

K. Falconer, Fractal geometry, John Wiley, 1990.

Ilmaisia ohjelmia fraktaalikuvien piirtämiseen

Mukavia ilmaisia fraktaalinpiirto-ohjelmia ovat esimerkiksi

• Fractint (Saatavana versiot Dos, Windows95 ja unix)

• Flarium (Win95)

• Fantastic Fractals 6.0 (Win95)

• Iterating on the Mac

Jouni Parkkonen
parkkone@math.jyu.fi

Solmu 3/1997-1998