Kongruenssi --
lukuteorian kätevä apuväline

Luvut 17 ja 32 antavat 5:llä jaettaessa saman jakojäännöksen 2. Sanotaan, että 17 ja 32 ovat kongruentteja modulo 5, merkitään 17 $\equiv$ 32  (mod 5). Koska kaikki mahdolliset jakojäännökset ovat 0,1,2,3,4, jokainen ei-negatiivinen kokonaisluku on kongruentti modulo 5 jonkin näistä luvuista kanssa.

Samoin määritellään yleisesti kongruenssi modulo m:

$$a \equiv b \pmod m$$ (1)

tarkoittaa, että luvut a ja b antavat m:llä jaettaessa saman jakojäännöksen eli yhtäpitävästi että erotus a-b on m:llä jaollinen (siis m:n kokonainen monikerta). Kun ajatellaan jälkimmäistä sanontaa, huomataan että a ja b saavat olla yhtä hyvin myös negatiivisia kokonaislukuja. Ilmeisesti jokainen kokonaisluku on kongruentti modulo m jonkin luvuista 0,1,$\dots$,m-1 kanssa. Esimerkiksi 81 $\equiv$ 0  (mod 9), -25 $\equiv$ 2  (mod 9).

Lukua m sanotaan kongruenssin (1) moduliksi. Jos a ei ole kongruentti luvun b kanssa modulo m, sanotaan, että a on epäkongruentti b:n kanssa modulo m ja merkitään a  $\not\equiv$ b  (mod m). Esimerkiksi 5  $\not\equiv$ 7  (mod 3).

Kongruenssin (1) merkitys on mukava ajatella myös muodossa "a on yhtäkuin b luvun m monikertaa vaille". Kyseessä onkin yhtälöä kovasti muistuttava relaatio. Sillä on ensiksikin seuraavat aivan ilmeiset ominaisuudet: (i) jokainen luku on kongruentti mod m itsensä kanssa, (ii) jos a $\equiv$ b  (mod m), niin b $\equiv$ a  (mod m), (iii) jos a $\equiv$ b  (mod m) ja b $\equiv$ c  (mod m), niin a $\equiv$ c  (mod m). Viimeisen ominaisuuden perusteella voidaan kongruensseja haluttaessa kirjoittaa myös "ketjuina": esimerkiksi -79 $\equiv$ -9 $\equiv$ 1 (mod 10), siis -79 $\equiv$ 1  (mod 10).

Analogia yhtälöiden kanssa menee vielä pitemmälle. Kongruenssiin voidaan lisätä sama luku molemmille puolille ja kongruenssia voidaan kertoa puolittain samalla luvulla. Näistä säännöistä on helppo varmistua, kun vähän miettii (1):n merkitystä.

Entä jakolasku? Yhtälön jakamisessa pitää muistaa varoa, ettei jakaja ole 0. Sama tietysti pätee kongruenssiinkin, mutta se ei vielä riitä. Esimerkiksi 15 $\equiv$ 9  (mod 6), mutta 3:lla jaettaessa saataisiin 5 $\equiv$ 3  (mod 6), joka ei pidä paikkaansa. Jakolaskua koskeva sääntö kuuluukin nyt näin: kongruenssi (1) voidaan jakaa puolittain luvulla, jolla ei ole modulin m kanssa yhteistä tekijää. Ajattele esimerkkinä äskeistä kongruenssia, jossa modulina on 6:n sijasta 2. (Säännön paikkansapitävyydestä yleisesti voi vakuuttua ajattelemalla (1):tä ja hajottamalla a-b alkutekijöihin.)

Lisää tutunnäköisiä sääntöjä: kongruenssit

$$a \equiv b \pmod m, \quad c \equiv d \pmod m$$

saa laskea puolittain yhteen ja kertoa puolittain, ts. näistä kongruensseista seuraa, että

$$a+c \equiv b+d \pmod m, \quad ac \equiv bd \pmod m.$$

Tästä voi varmistua kirjoittamalla yhtälöt

$$(a+c)-(b+d) = (a-b)+(c-d), \quad ac-bd = a(c-d)+(a-b)d,$$

joissa kummassakin oikea puoli on nyt m:n monikerta.

Jos a $\equiv$ b  (mod m) ja P(x) on x:n kokonaiskertoiminen polynomi, niin edellisten sääntöjen nojalla P(a) $\equiv$ P(b) (mod m). Näin on saatu käytännöllinen korvaussääntö: korvattaessa a kongruentilla luvulla myös a:n jokaisen kokonaiskertoimisen polynomin arvo korvautuu kongruentilla luvulla. Esimerkiksi

$$\begin{split} 3\cdot 6^{13} - 18\cdot 6 ^5 + 6 ^2 & \equiv 3(... ... ^5 + (-1) ^2 \\ & \equiv -3+4+1 \equiv 2 \pmod 7. \end{split}$$

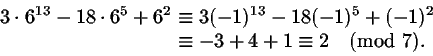
Tässä ei siis luvun 6 korkeita potensseja tarvinnut lainkaan laskea. Tämä onkin yksi kongruenssilaskujen etu: selvitään luvuilla, jotka eivät ole kovinkaan paljon suurempia kuin moduli m.

Esimerkki. Mikä on luvun 2¹⁹⁹⁸ jakojäännös jaettaessa 11:llä?

Koska 2⁵ = 32 $\equiv$ -1  (mod 11), niin 2¹⁰ $\equiv$ 1 ja siis 2¹⁹⁹⁰ $\equiv$ 1  (mod 11). Edelleen 2⁸ = 2⁵$\cdot$2³ $\equiv$ -8 $\equiv$ 3  (mod 11), joten saadaan 2¹⁹⁹⁸ $\equiv$ 3  (mod 11). Vastaus on siis 3.

Kongruenssit otti ensimmäisenä käyttöön Gauss, jonka kirja Disquisitiones Arithmeticae (vuodelta 1801) oli huima askel lukuteorian ja algebran kehityksessä. Nykyisin kongruensseilla on käyttöä monissa sovelluksissa. Matematiikkaa soveltavissa kirjoissa kongruenssilaskennasta käytetään usein nimitystä modular arithmetic. Tietokoneille tällainen laskenta sopii erinomaisesti, koska laskuissa tarvittava lukujoukko voidaan jo etukäteen rajata tietyn kokoiseksi.

Diofantoksen yhtälöistä

Mitkä kokonaisluvut x,y toteuttavat yhtälön

$$\mbox{}x^2-4y^2 = 5 ?$$

Tällaista yhtälöä, jolle etsitään kokonaislukuratkaisuja, sanotaan Diofantoksen yhtälöksi.

Pienellä kokeilulla huomataan, että yhtälö toteutuu arvoilla x =3, y = 1. Niinpä sillä on ainakin ratkaisut (x,y) = ($\pm$3,$\pm$1). Ovatko nämä kaikki ratkaisut? Tällä kertaa kaikkien ratkaisujen löytäminen on helppoa, sillä yhtälö voidaan kirjoittaa muotoon

$$\mbox{} (x-2y)(x+2y)=5.$$

Esittämällä luku 5 kokonaislukujen tulona muodossa 5 = 1$\cdot$5 ja muodossa 5 = (-1)(-5) sekä ratkaisemalla näin syntyvät yhtälöparit

$$\left\{\aligned x-2y&=1\\ x+2y&=5,\endaligned\right. \qquad\qquad \left\{\aligned x-2y&=-1\\ x+2y&=-5\endaligned\right.$$

päädytään ratkaisuihin (3,1) ja (-3,-1). Mieti itse, miten saadaan ratkaisut (3,-1) ja (-3,1). Koska luvulla 5 ei ole muita kokonaislukuhajotelmia, ei myöskään muita ratkaisuja voi tulla.

Diofantoksen yhtälöitä ratkaistaessa voivat tulokset tietysti olla periaatteessa kolmenlaisia: yhtälöllä ei ole yhtään ratkaisua, yhtälöllä on äärellinen määrä ratkaisuja tai yhtälöllä on äärettömän monta ratkaisua. Seuraava yhtälö voi näyttää edellistä vaikeammalta:

$$\mbox{} x^2-5y^2=2.$$

Kokeilemalla ratkaisuja ei löydy. Tosin esimerkiksi (x,y) = (9,4) näyttää melko lupaavalta, sillä 9²-5$\cdot$4² = 1. Tosiasiassa tällaisesta havainnosta ei kuitenkaan ole mitään apua.

Tässä tapauksessa avuksi tulevat kongruenssit. Jos x ja y toteuttavat mainitun yhtälön, niin tietysti myös x²-5y² $\equiv$ 2  (mod m), olipa m mikä hyvänsä moduli. Valitaan m = 4. Jokaisen parillisen luvun neliö on $\equiv$ 0  (mod 4) ja parittoman luvun neliö $\equiv$ 1  (mod 4). Tästä nähdään, että x²-5y² on kongruentti luvun 1, 0 tai -1 kanssa mod 4. Mikään näistä ei ole $\equiv$ 2  (mod 4). Näin ollen yhtälöllä x²-5y² = 2 ei ole kokonaislukuratkaisua.

Maallikko voisi ajatella, että tehokkaalla tietokoneella olisi saatu sama tulos ilman matemaattisia pohdintoja. Koneellahan voi testata lyhyessä ajassa kaikki kokonaisluvut hyvinkin suureen rajaan asti. Mutta kuinka suureen rajaan oikeastaan olisi mentävä? Tätä voi miettiä vaikkapa seuraavan esimerkin valossa: Diofantoksen yhtälöllä x²-991y² = 1 on äärettömän monta ratkaisua mutta ensimmäinen positiivinen y:n arvo, jolla ratkaisu saadaan, on suurempi kuin 10²⁸.

Tehtävä. Tutki, onko yhtälöillä

$$x^3+y^3+z^3=20,\qquad \qquad x^3+y^3+z^3=22$$

(kummallakin erikseen) kokonaislukuratkaisua (x,y,z). Jos ratkaisua ei tunnu löytyvän kokeilemalla, yritä osoittaa, ettei ratkaisua voikaan olla. Korvaa sitä varten yhtälö vastaavalla kongruenssilla mod m, missä m on sopivasti valittu moduli.

Kelpaisivatko kongruenssit myös antamaan tuloksen, että jollain Diofantoksen yhtälöllä on ratkaisu? Eli onko yhtälöllä P(x,y,$\dots$) = 0 ratkaisu, jos kongruensseilla P(x,y,$\dots$)$\equiv$ 0 (mod m) on ratkaisu tarpeeksi monella modulilla m? Jälkimmäinen probleemahan voidaan joka tapauksessa ratkaista äärellisellä määrällä kokeiluja (kullakin modulin arvolla). Vastaus kysymykseen on valitettavasti kielteinen. On jopa mahdollista, että kongruensseilla on ratkaisut kaikilla moduleilla m, mutta yhtälö on ratkeamaton.

Mutta tämänkään probleeman kohdalla matemaatikot eivät ole luovuttaneet. Käyttämällä ns. p-adisia lukuja, joiden käsite liittyy kongruensseihin, on monissa tapauksissa onnistuttu saamaan tehokkaita riittäviä ehtoja Diofantoksen yhtälöiden ratkeavuudelle. Tässä ei voida sanoa p-adisista luvuista enempää kuin että niistä on tullut tärkeä osa modernia lukuteoriaa ja algebraa.

Fermat'n pikku lause

Seuraava tulos on peräisin Fermat'lta 1600-luvulta.

Lause Jos p on alkuluku ja a on kokonaisluku, joka on p:llä jaoton, niin

$$a^{p-1} \equiv 1 \pmod p.$$

Siis esimerkiksi 2¹⁰ $\equiv$ 1  (mod 11), mikä jo todettiinkin edellä olleessa esimerkissä. Samoin luvut 3¹⁰, 4¹⁰,$\dots$, 10¹⁰ ovat $\equiv$ 1  (mod 11). Tulosta sanotaan Fermat'n pikku lauseeksi, koska nimitys "Fermat'n lause" viittaisi kuuluisaan Fermat'n suureen lauseeseen, joka onnistuttiin todistamaan vasta 1994. Pikku lauseen seuraukset (matemaattisessa mielessä) ovat paljon merkittävämpiä kuin suuren lauseen!

Lauseen todistamiseksi ajatellaan luku a kerrotuksi vuorotellen luvuilla 1,2,$\dots$,p-1. Jokainen näin saatu tulo ka on kongruentti mod p jonkin luvuista 1,2,...,p-1 kanssa:

$$ka \equiv c_k \pmod p, \qquad 1 \le c_k \le p-1 \qquad (k=1,2,\dots,p-1).$$

Jos kaksi tuloa ovat kongruentteja, ka $\equiv$ k'a  (mod p), niin kongruenssi voidaan jakaa luvulla a (koska a on p:llä jaoton) ja saadaan k $\equiv$ k'  (mod p), siis k = k'. Eri k:n arvoja vastaavat siis eri luvut c_k. Tästä nähdään, että c_k:t ovat jälleen luvut 1,2,$\dots$,p-1, nyt jossain uudessa järjestyksessä. Kun siis kerrotaan kaikki mainitut kongruenssit keskenään, tuloksena on

$$1\cdot 2\cdots (p-1)\cdot a^{p-1} \equiv 1\cdot 2\cdots (p-1) \pmod p.$$

Tässä voidaan jakaa luvulla 1$\cdot$24...(p-1). Silloin jäljelle jää juuri lauseen kongruenssi.

Fermat'n pikku lausetta on sovellettu mm. salakirjoitusmenetelmissä.

Nykyisiin tiedon salausmenetelmiin liittyy myös läheisesti kysymys alkulukutestauksesta: miten saadaan selville, onko annettu suuri luku N alkuluku? Tehokkaiden testausmenetelmien löytäminen on kuuma kysymys meneillään olevassa kilpajuoksussa, jossa koko ajan parannetaan toisaalta salaustapoja ja toisaalta salauksen murtamistapoja.

Voitaisiinko edellä olevaa lausetta käyttää alkulukutestauksessa? Ilmeisesti sillä saadaan ainakin kielteinen tulos: jos esimerkiksi 2 ^N-1  $\not\equiv$ 1  (mod N), niin N ei ole alkuluku. Tämä voi sitäpaitsi olla laskennallisesti melko tehokaskin tapa tutkia asiaa; muista ettei 2:n potenssia tarvitse laskea sellaisenaan vaan ainoastaan modulo N.

Entä jos 2 ^N-1 $\equiv$ 1  (mod N)? Tästä ei vielä seuraa, että N olisi alkuluku. Esimerkiksi luku N = 341 täyttää tämän ehdon (hajota se alkutekijöihin). Näitä lukuja nimitetään valealkuluvuiksi, tarkemmin sanottuna kannan 2 suhteen.

Menetelmää voidaan parantaa laskemalla a ^N-1  (mod N) myös suuremmilla kantaluvun a arvoilla. Jos esimerkiksi 2 ^N-1 $\equiv$ 1 mutta 3 ^N-1  $\not\equiv$ 1  (mod N), niin N ei voi olla alkuluku. Asiaa tarkemmin tutkittaessa kylläkin huomattiin, että on olemassa sellaisiakin tapauksia, joissa N ei ole alkuluku mutta

$$a^{N-1} \equiv 1 \pmod N$$

aina, kun luvuilla a ja N ei ole yhteisiä tekijöitä. Tällaisia poikkeuksellisia lukuja N sanotaan Carmichaelin luvuiksi. Pienin Carmichaelin luku on 561. Pitkään oli selvittämättä, onko näitä lukuja vain äärellinen määrä vai löytyykö niitä rajattomasti. Muutama vuosi sitten tämä kysymys kuitenkin sai ratkaisunsa: Carmichaelin lukuja on äärettömän paljon.

Tauno Metsänkylä
taumets@utu.fi

Solmu 3/1997-1998