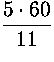Solmun 2/96-97 tehtävien ratkaisut

Muutamissa tehtävissä oli painovirheitä. Tehtävät on tässä esitetty ratkaisujen yhteydessä uudelleen.

21. Kellon osoittimet ovat päällekkäin kello 12. Milloin ne ovat seuraavan kerran päällekkäin?

Ratkaisu. Kellon minuuttiosoittimen kiertonopeus on (yksikkönä kierrosta tunnissa) 1 ja tuntiosoittimen $\displaystyle {1\over 12}$. Aika, joka kuluu osoittimien kahden päällekkäinolon välillä olkoon x. Tänä aikana minuuttiosoitin tekee x kierrosta ja tuntiosoitin $\displaystyle {x\over 12}$ kierrosta. Koska osoittimet ovat päällekkäin, minuuttiosoitin on siirtynyt edellisestä päällekkäinolosta saman verran kuin tuntiosoitin ja lisäksi yhden täyden kierroksen. Siis x=1+$\displaystyle {x\over 12}$ eli t=$\displaystyle {12\over 11}$. 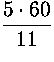Tämä aika on 1 t $\displaystyle {60\over 11}$ min eli 1 t 5 min $\displaystyle {5\cdot 60\over 11}$ s eli 1 t 5 min 27,3 s. Osoittimet ovat kello 12:n jälkeen seuraavan kerran päällekkäin kello 13.05.27.

22. Todista, että kolmen peräkkäisen kokonaisluvun kuutioiden summa on jaollinen kolmella.

Ratkaisu. (a-1)3+a3+(a+1)3=a3-3a2+3a-1+a3+a3+3a2+3a+1=3a3+6a=3(a3+2a).

23. Todista, että 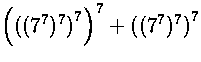$\left(\left((7^7)^7\right)^7\right)^7+\left((7^7)^7\right)^7$ on jaollinen 10:llä.

Ratkaisu. Kymmenellä jaollisuuden kannalta vain luvun viimeisellä numerolla on merkitystä. Samoin kahden luvun tulon viimeiseen numeroon vaikuttaa vain viimeisten numeroiden tulo. Koska 72=49, 73 päättyy samaan numeroon kuin $7\cdot 9=63$ ja 74 samaan numeroon kuin $9\cdot 9=81$. Edelleen 77 päättyy samaan numeroon kuin $1\cdot 3=3$.Tästä seuraa, että (77)7 päättyy samaan numeroon kuin 37. Nyt 33=27 ja 34=81, joten 37 päättyy 7:ään. 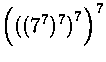Tämän perusteella nähdään heti, että $\left((7^7)^7\right)^7$ päättyy 3:een ja $\left(\left((7^7)^7\right)^7\right)^7$ taas 7:ään. Koska 3+7=10, tehtävässä kysytty luku päättyy 0:aan, joten se on 10:llä jaollinen.

24.. Osoita, että a(a+1)(a+2)(a+3)+1 on kaikilla kokonaisluvuilla a kokonaisluvun neliö.

Ratkaisu. a(a+1)(a+2)(a+3)+1 = a(a+3)(a2+3a+2)+1 = a(a+3)(a(a+3)+2)+1 = (a(a+3))2+2a(a+3)+1 = (a(a+3)+1)2.

25. Ratkaise yhtälöryhmä

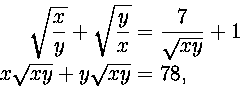
\begin{displaymath} \begin{split} \sqrt {\displaystyle {x\over y}}+\sqrt {\displ... ...r \sqrt {xy}}+1\ x\sqrt {xy}+y\sqrt {xy} &= 78,\ \end{split} \end{displaymath}

missä x>0, y>0.

Ratkaisu. Merkitään $\sqrt {xy}=t$. Kun ensimmäinen yhtälö lavennetaan t:llä, saadaan ryhmä

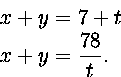
\begin{displaymath} \begin{split} x+y&=7+t\ x+y&={78\over t}.\ \end{split}\end{displaymath}

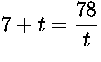Siis $7+t=\displaystyle {78\over t}$, joten t:n on oltava toisen asteen yhtälön t2+7t-78=0 ratkaisu. Tällä yhtälöllä on kaksi ratkaisua t=-13 ja t=6; vain jälkimmäinen voi kelvata. Kun t=6, alkuperäinen yhtälöryhmä saa muodon

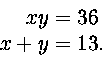
\begin{displaymath} \begin{split} xy&=36\ x+y&=13.\ \end{split}\end{displaymath}

Tämän yhtälöryhmän ratkaisut ovat x=9, y=4 ja x=4, y=9. Nämä toteuttavat myös alkuperäisen yhtälöryhmän.

26. Todista, että viiden peräkkäisen kokonaisluvun neliöiden summa on jaollinen viidellä, muttei jaollinen 25:llä.

Ratkaisu. Olkoon a kokonaisluku. Silloin (a-2)2+(a- 1)2+a2+(a+1)2+(a+2)2=5a2+10=5(a2+2). Tämä on jaollinen 5:llä. Jotta se olisi jaollinen 25:llä, olisi luvun a2+2 oltava jaollinen 5:llä. Mutta a2 voi päättyä vain numeroihin 0, 1, 4, 9, 5 tai 6 (vain viimeinen numero vaikuttaa neliön viimeiseen numeroon; vain luetellut numerot esiintyvät lukujen 0, 1, 2, ..., 9 neliöiden viimeisinä numeroina). Siis a2+2 päättyy johonkin numeroista 2, 3, 6, 1, 7, 8, eikä ole 5:llä jaollinen.

27. Onko olemassa kokonaislukuja m ja n, jotka toteuttavat yhtälön m2+1958=n2?

Ratkaisu. Jos tällaiset kokonaisluvut olisivat olemassa, olisi (n-m)(n+m)=n2-m2=1958=2$\cdot$979. Lukujen n ja m on oltava joko molempien parillisia tai molempien parittomia. Kummassakin tapauksessa n-m ja n+m ovat parillisia, joten niiden tulo on jaollinen 4:llä. Koska 1958 ei ole jaollinen neljällä, lukuja n ja m ei ole olemassa.

28. Sievennä lauseke

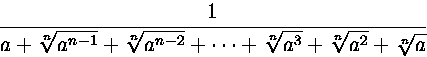
\begin{displaymath} {1\over a+\root n\of{a^{n-1}}+\root n\of {a^{n-2}}+\cdots+\root n\of {a^3}+\root n\of {a^2}+\root n\of a} \end{displaymath}

sellaiseen muotoon, että nimittäjässä ei esiinny juurilausekkeita.

Ratkaisu. Merkitään a1/n=b. Sievennettävä lauseke on

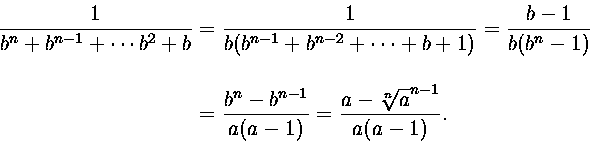
\begin{displaymath} \begin{split} {1\over b^n+b^{n-1}+\cdots b^2+b} &= {1\over b... ...\over a(a-1)} = {a-\root n\of a^{n- 1}\over a(a-1)}.\end{split}\end{displaymath}

29. Merkitään luvun x 10-kantaista logaritmia $\log x$:llä. Laske $\log 48$ lukujen $\log_35=a$ ja $\log_58=b$ avulla.

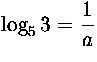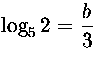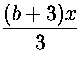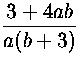Ratkaisu. Oletuksista seuraa, että $\log_53=\displaystyle{1\over a}$ ja $\log_52=\displaystyle{b\over 3}$.Olkoon $x=\log 48$ eli $5^{1/a}\cdot 5^{4b/3}=$ $3\cdot 2^4=48=$ $\displaystyle{10^x=}$ $\displaystyle{2^x5^x}$ $\displaystyle{=5^{(bx+3x)/3}}$. Siis $\displaystyle{1\over a}$+$\displaystyle{4b\over 3}$=$\displaystyle{(b+3)x\over 3}$, josta ratkaistaan x=$\displaystyle{3+4ab\over a(b+3)}$.

30. Ratkaise yhtälö $\sin^4x+\cos^4x=\cos 4x$.

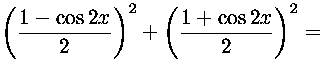
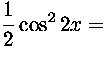
Ratkaisu. Käytetään kaksinkertaisen kulman kosinin kaavaa yhtälön vasemmalla puolella kulmaa kasvattamaan ja oikealla puolella pienentämään: $\sin^4x+\cos^4x=$$(\sin^2x)^2+(\cos^2x)^2=$$\left(\displaystyle {1- \cos 2x\over 2}\right)^2+ \left(\displaystyle {1+\cos 2x\over 2}\right)^2=$$\displaystyle {1\over 2}$+$\displaystyle {1\over 2}\cos^22x=$$\displaystyle {2cos^22x-1}$. 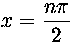Yhtälö palautuu siis yhtälöksi $\cos^22x=1$, $\cos 2x=\pm 1$, $2x=n\pi$, $x=\displaystyle {n\pi\over 2}$; nämä luvut toteuttavat alkuperäisen yhtälön.

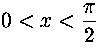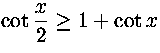
31. Todista: kun $0<x<\displaystyle {\pi\over 2}$, niin $\cot\displaystyle {x\over 2}\ge 1+\cot x$

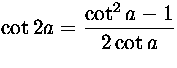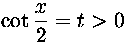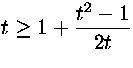Ratkaisu. Tunnetusti $\cot 2a=\displaystyle {\cot^2a-1\over 2\cot a}$. Merkitään $\cot \displaystyle {x\over 2}=t\gt$. Todistettava epäyhtälö on yhtäpitävä epäyhtälön $t\ge 1+\displaystyle {t^2-1\over 2t}$eli $2t^2\ge 2t+t^2-1$ eli $(t-1)^2\ge 0$ kanssa. Viimeinen epäyhtälö on aina tosi, joten tehtävän epäyhtälökin on voimassa.

32. Piirretään ympyrä niin, että se sivuaa tasakylkisen kolmion kylkiä ja kolmion a-pituinen kanta on ympyrän jänne. Määritä ympyrän säde r a:n ja kolmion korkeuden h avulla.

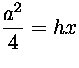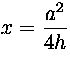Ratkaisu. Kolmion kärjet B ja C ovat samalla ympyrän ja kolmion ABC kylkien sivuamispisteet. Olkoon ympyrän keskipiste O ja D janojen BC ja AO leikkauspiste; olkoon OD=x. Suorakulmaisesta kolmiosta ACO saadaan $\displaystyle{a^2\over 4}=hx$ eli $x=\displaystyle{a^2\over 4h}$. Suorakulmaisesta kolmiosta CDO saadaan nyt 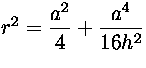$r^2=\displaystyle{a^2\over 4}+\displaystyle{a^4\over 16h^2}$, josta r on helposti laskettavissa.

33. Laske suorakulmaisen kolmion suoran kulman puolittajan pituus kolmion kateettien a ja b avulla.

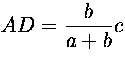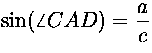Ratkaisu. Olkoon ABC suorakulmainen kolmio ja CD sen kulmanpuolittaja. Koska kulmanpuolittaja jakaa vastaisen sivun viereisten sivujen suhteessa, $AD=\displaystyle{b\over a+b}c$. Koska $\angle ACD=45^\circ$ja $\sin(\angle CAD)=\displaystyle{a\over c}$, saadaan sinilauseesta sovellettuna kolmioon ADC 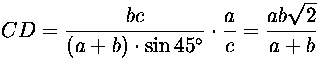$CD=\displaystyle{bc\over (a+b)\cdot \sin 45^\circ}\cdot \displaystyle{a\over c}=\displaystyle{ab\sqrt 2\over a+b}$.

34.Ympyrällä, neliöllä ja tasasivuisella kolmiolla on sama ala. Laske näiden kuvioiden piirien suhde.

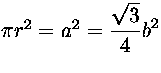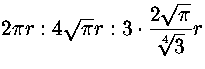Ratkaisu. Ympyrän säde r, neliön sivu a, tasasivuisen kolmion sivu b. Tiedetään, että $\pi r^2=a^2=\displaystyle{\sqrt 3\over 4}b^2$. Piirien suhteet ovat $2\pi r :4\sqrt{\pi}r:3\cdot \displaystyle{2\sqrt {\pi}\over \root 4\of 3} r$.

35. Määritä se ympyrän keskuskulma, jota vastaavan segmentin jänne on yhtä pitkä kuin segmentin sisään piirretyn mahdollisimman suuren ympyrän piiri.

Ratkaisu. Olkoon isomman ympyrän säde R ja keskipiste O; olkoon jänteen AB erottamaan segmenttiin piirretyn mahdollisimman suuren ympyrän säde r; tämä ympyrä sivuaa AB:tä pisteessä N ja kaarta AB pisteessä M. Leikatkoon suora MNO isomman ympyrän myös pisteessä F. Pisteen N potenssi ympyrän suhteen on 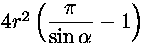$\pi^2r^2=2r\cdot NF=2r(2R- 2r)=$$4r^2\left(\displaystyle{\pi\over \sin\alpha}-1\right)$. Tästä 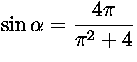$\sin\alpha=\displaystyle{4\pi\over \pi^2+4}$. 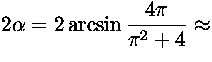Kysytty keskuskulma on $2\alpha=2\arcsin\displaystyle{4\pi\over \pi^2+4}\approx$$ 130^\circ$.

Matti Lehtinen

[email protected]

Solmu 2/1996-1997