Pál Erdösin matematiikasta

Edellisessä solmussa oli Marjatta Näätäsen kirjoitus Pál Erdösistä. Siitä ilmeni oivallisesti, että Erdös oli todellinen nukkavierun professorin karikatyyri. Vaikka hyväksyttäisiinkin se seikka, että matemaatikot poikkeavat toisistaan luonteeltaan vähintään yhtä paljon kuin ihmiset yleensäkin, jäljelle jää kysymys, miten jokin tieteenala voi lumota tieteilijän niin, että hän omistautuu sille täysin, elää askeettisesti ja suhtautuu arkipäiväisiin asioihin suorastaan välipitämättömästi. Erdösin tapauksessa kysymykseen on tavallista helpompi vastata, sillä hänen työpanoksensa kohdistui aloille, joiden tutkimusongelmien ymmärtämiseen riittää hyvä matemaattinen yleissivistys.

Erdösin tuotanto oli ennenkuulumattoman laaja, toista tuhatta artikkelia. Tätä kannattaa verrata siihen, että useilla matematiikan aloilla jo yhden artikkelin julkaisemista vuodessa pidetään hyvän tutkijan merkkinä. Vaikka Erdös tuskin oli vuosisadan huomattavin matemaatikko, ja tuotteliaisuuteenkin nähden on esitettävä se varaus, että laatu on usein määrää tärkeämpi tekijä, Erdös oli kiistatta kaikkien aikojen yhteistyökykyisin matemaatikko: hänellä oli yhteisjulkaisuja ainakin neljän sadan muun tutkijan kanssa. Erdösin tuotannon kattavan tarkastelun sijasta on joka tapauksessa järkevintä tyytyä yhteen, anekdoottimaiseen, mutta jollain tavalla tyypilliseen esimerkkiin.

Erdös havainnollisti matematiikan, tai oikeastaan nimenomaisesti todistamisen, voimaa seuraavan väitteen avulla.

"Mielivaltaisesta 6 hengen ryhmästä voidaan valita 3, jotka ovat joko kaikki keskenään tuttuja tai joista kukaan ei tunne ketään toista."

Tuttuus oletetaan luonnollisesti molemminpuoliseksi. Miten moinen väite todennetaan? Helppoa, voisi ajatella, käydään vain läpi kaikki tapaukset. Kunkin parin kohdalla on kaksi mahdollisuutta: joko ao. henkilöt tuntevat toisensa tai eivät. Parin voi kuuden hengen joukosta valita eri tavalla. Siis tarkasteltavia tapauksia on kappaletta. Tässä vaiheessa halukkuus väitteen tapaus tapaukselta tutkimiseen laimennee huomattavasti.

Väitteen voi kuitenkin suoraan todistaa oikeaksi. Olkoon nimittäin A yksi tarkasteltavista kuudesta henkilöstä. Tuttuus ja tuntemattomuus ovat sikäli symmetrisessä asemassa, että henkilön A voi olettaa tuntevan vähintään puolet muista, siis vähintään kolme henkeä; olkoot nämä B, C ja D. Jos kukaan näistä ei tunne toisiaan, on kolmen toisiaan tuntemattoman joukko. Muuten esimerkiksi B tuntee C:n, ja on kolmen tutun joukko. Näin väite on todistettu. Mainittakoon, että juuri tämä oli tehtävänä yhdysvaltalaisessa Putnam-kilpailussa vuonna 1953.

Tietokoneesta innostunut saattaisi protestoida, että tapauskohtaisen ratkaisutavan hylkääminen oli hätiköityä. 32768 tapausta on tosin ihmiselle raskas urakka, mutta nykymikrolle vain silmänräpäys. Kritiikki on kuitenkin aiheetonta, koska käsittelemämme väite yleistyy. Niinpä samanlaisin ideoin voidaan osoittaa, että 18 hengen joukosta voidaan aina valita 4 tutun tai 4 toisiaan tuntemattoman joukko, ja tapausta riittänee nujertamaan kaikki tietokoneet, vaikka ilmiselvästi samanlaiset tapaukset onnistuttaisiin yhdistelemään.

Yleisesti voidaan osoittaa, että hengen joukosta voidaan valita n tutun tai n toisiaan tuntemattoman joukko, kun . Luonnollisestikaan tuloksen pätevyys ei rajoitu vain ihmisiin ja keskinäiseen tuttuuteen, vaan yhtä hyvin voitaisiin käsitellä esim. kaupunkeja ja niiden välisiä suoria junayhteyksiä. Tavallisesti asia esitetäänkin abstraktimmin verkkoteoreettisesti, ja ihmisten ja tuttuuden sijasta puhutaan solmuista ja särmistä.

Yllä oleva verkko on , missä on solmujen joukko ja

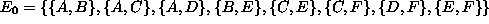
särmien joukko. Verkon voi ajatella kuvaavan kuutta henkeä ja sitä, että A tuntee henkilöt B, C ja D, E B:n, C:n ja F:n sekä F C:n ja D:n. Kun G=(V,E) on mielivaltainen verkko, niin joukkoa kutsutaan verkon G klikiksi, jos sen jokainen solmu on toiseen yhteydessä, ts. jos kaikilla eri . Vastaavasti on riippumaton joukko, jos sen solmujen välillä ei ole lainkaan särmiä, ts. kaikilla . Verkossa esimerkiksi on klikki ja riippumaton. Näiden käsitteiden avulla voidaan muotoilla

Ramseyn lause: Jokaista vastaa sellainen , että jos verkossa G=(V,E) on vähintään r solmua, niin G sisältää n solmun klikin tai n solmun riippumattoman joukon.

Lause on nimetty Frank Ramseyn mukaan, joka vuonna 1930 esitti sen hieman yleisemmässä muodossa kuin yllä. Edellä on jo todettu, että lauseessa voidaan valita . Kun , merkitään R(n):llä pienintä lukua r, jolle lauseen ehto on voimassa. Putnam-kilpailussakin esitetty tapaus osoitti, että . Itse asiassa yhtäsuuruus on voimassa, R(3) = 6, sillä 5 solmun verkossa ei välttämättä ole kolmen solmun klikkiä tai riippumatonta joukkoa, kuten alla oleva viisikulmio osoittaa.

Tiedetään, että R(4) = 18, mutta suuremmilla argumenttien arvoilla nämä ns. Ramseyn funktion arvot eivät ole tarkasti tiedossa, esim. . Itse asiassa tarkkojen arvojen etsiminen on osoittautunut niin työlääksi, että se hädin tuskin vastaa tarkoitustaan. Sen sijaan asymptoottiset arviot, kuten yläraja , ovat periaatteellisesti tärkeitä.

Tässä kohdassa Erdös palaa kuvaan, hän näet esitti Ramseyn funktiolle erittäin hyvän alarajan vuonna 1947. Ongelma piilee sopivien esimerkkiverkkojen löytymisessä. Jos nimittäin r solmun verkossa ei ole n solmun klikkiä eikä n solmun riippumatonta joukkoa, niin Ramseyn funktion määritelmän mukaan R(n) > r. Sopivia verkkoja on kuitenkin vaikea konstruoida, sillä ihmisillä on taipumus sisällyttää esimerkkeihin aina tietty määrä säännöllisyyttä, mikä edistää klikkien ja riippumattomien joukkojen syntymistä. Erdös oivalsi, että pulman voi kiertää valitsemalla verkko satunnaisesti. Kiinnitetään ensin tarkasteltavat ja r solmun joukko, vaikkapa . Sen jälkeen käydään läpi kaikki solmuparit yksitellen, ja jokaisen kohdalla arvotaan kruunaa ja klaava heittäen, yhdistetäänkö parin solmut vai ei. Jos joukossa on n solmua, se on klikki todennäköisyydellä ja riippumaton joukko samoin todennäköisyydellä . Arvotun verkon G kaikkien n solmun klikkien ja riippumattomien joukkojen lukumäärän X odotusarvo on siis

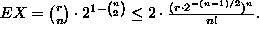
Erityisesti tapauksessa ja saadaan

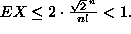
Mutta tämä odotusarvohan ei voi olla pienempi kuin yksi, ellei satunnaismuuttuja X saa nollasta poikkeavalla todennäköisyydellä arvoa nolla. Tämä taas merkitsee, että ennemmin tai myöhemmin arvonta tuottaa r solmun verkon, jossa ei ole n solmun klikkejä eikä riippumattomia joukkoja. Siis

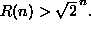
Erdösin oivallus oli todellinen Kolumbuksen muna, ja sen arvoa lisää se, että konstruktiivisesti muodostettuja verkkoja käyttäen Ramseyn funktiolle ei ole pystytty todistamaan eksponentiaalisia alarajoja. Erdösin todistus oli lähtölaukaus satunnaismenetelmien käytölle kombinatoriikassa.

Kirjallisuutta: Erdösin tulos julkaistiin vuonna 1947 lehdessä Bulletin of American Mathematical Society (vol. 53, sivut 292-294). Kirjoituksen alasta on kattava kuvaus kirjassa R. L. Graham, B. L. Rothschild ja J. H. Spencer: Ramsey Theory, Wiley, 1980. Lukua R(5) koskevat arviot perustuvat edellisen lisäksi artikkeliin B. D. McKay, S. Radziszowski: R(5,4)=25 lehdessä Journal of Graph Theory 19 (1995), sivut 309-322.

Kerkko Luosto