Lisää Eulerin kaavasta
Tutustumme lopuksi 2-ulotteisten pintojen luokitteluun Eulerin kaavaan
nojautuen. Tarvittavat käsitteet ja argumentit esitellään intuitiivisesti.
Niiden tarkka matemaattinen määrittely ja todistusten läpivienti niiden avulla
olisikin tutkija-tasoista yliopistomatematiikkaa. Tässä on tarkoitus saada
ainoastaan yleiskuva asiasta.
Tutkimme konkreettisten 3-ulotteisten kappaleitten 2-ulotteisia pintoja.
Tahko-särmä-kärki-rakenne ajatellaan pinnalle piirretyksi viivoitukseksi,
jossa pinta jakaantuu monikulmioiden kaltaisiin alueisiin, joita pidetään
tahkoina. Alueiden reunat muodostuvat särmistä, joiden ei tarvitse olla
suoraviivaisia. Särmien risteyskohtia pidetään kärkinä. Särmillä on
kärjet päätepisteinä. Päätepisteet voivat yhtyä, jolloin särmä on
sulkeutuva rengas. Yhtyneet päätepisteet lasketaan yhdeksi kärjeksi.
Oletamme lisäksi, että pinnoilla on seuraava suunnistusominaisuus:
särmiä piirtäessämme pysymme koko ajan joko kappaleen ulkopinnalla tai
kappaleen sisäpinnalla, mutta emme pääse huomaamattomasti liukumaan ulkoa
sisään tai päinvastoin. Tämän voi sanoa hieman matemaattisemmin seuraavasti:
jos annamme kappaleen pinnan normaalivektorin kulkea kappaleen pintaa pitkin
minkä tahansa lähtöpisteeseen palaavan reitin, on vektori takaisin palattuaan
samoin päin kuin lähtiessä. Esimerkiksi Möbiuksen nauhalla ei ole tätä
ominaisuutta. Sen pinnalta löytyy reitti, jota pitkin kulkien vektori on yhden
kierroksen jälkeen ylösalaisin.
Merkitään seuraavassa lausekkeen T - S + K arvoa E:llä. E:tä kutsutaan
pinnan Euler-karakteristikaksi. Todistamme induktiolla, että
E(pallo) = 2.
Piirretään pallon pinnalle kiinteästä pisteestä alkaen sulkeutuva rengas.
Pallon pinta jakaantuu 2:ään tahkoon, joita rajoittaa 1 särmä. Valittu
kiinteä alkupiste on kärki. Täten
T - S + K =
2 - 1 + 1 = 2, eli Eulerin
kaava toteutuu tässä tapauksessa.
Oletetaan pallon pinta viivoitetuksi niin, että
T - S + K = 2. Käydään
läpi kaikki mahdolliset tavat muuttaa lukumääriä T,
S ja K ja
osoitetaan,
että lausekkeen T - S + K
arvo pysyy
vakiona. Tässä malliksi yksi tapaus:
Olkoon erään tahkon reunalla p kärkeä. Valitaan tahkon
sisältä piste
uudeksi kärjeksi ja yhdistetään se tahkon reunalla oleviin kärkiin
toisiaan leikkaamattomilla viivoilla. Tällöin T, S
ja K muuttuvat
seuraavasti:
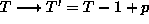
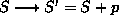
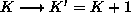
Välittömästi nähdään, että
T' - S' + K' =
T - S + K = 2. Käy läpi
yksityiskohtaisesti kaikki muut mahdollisuudet muuttaa T:n,
S:n ja K:n
lukumääriä.
Koska kaava pitää paikkansa 1-kohdan tapauksessa ja kohdan 2
reformaatiot eivät muuta lausekkeen E arvoa, kaava on tosi
kaikille
mahdollisille pallopinnan viivoituksille.
Pallon voi takoa eri muotoihin, kunhan ei revi sitä eikä
tee reikiä. Tahkojen, särmien ja kärkien lukumäärät säilyvät ja näin
kaikille pallon kaltaisille pinnoille
E(pinta) =
T - S + K = 2.
![[Torus]](torus.jpg)
Munkkirinkilän eli toruksen Euler-karakteristikalla on toinen arvo.
Liimaamalla suorakulmion mallinen paperi lieriöpinnaksi ja liittämällä
lieriön päät yhteen nähdään toruksen pinnalla viivoitus, jossa on 1 kärki
(suorakulmion kärjet yhtyvät siinä), 2 särmää (molemmat liimaussaumat)
ja 1 tahko (koko suorakulmio), joten
E(torus) =
1 - 2 + 1 = 0.
Induktio toimii samoin kuin pallon tapauksessa.
Torus-pinta voidaan ajatella syntyneeksi myös niin, että liitetään
pallopintaan yksi kahva ja muotoillaan näin saatu pinta munkkirinkilän
näköiseksi. Kahvaksi kelpaa lieriöpinta, jonka päät muotoillaan niin, että
ne tulevat yhteneviksi kahden pallon pinnalla olevan erillisen tahkon kanssa.
Taitetaan lieriö sopivasti, liitetään sen päät valittuihin tahkoihin ja
piirretään särmä ensimmäisen tahkon reunalla olevasta kärjestä toisessa
päässä olevan tahkon reunalla olevaan kärkeen. Tällöin tahkojen määrä
vähenee yhdellä ja särmien määrä vastaavasti kasvaa yhdellä, joten
Euler-karakteristikan arvo pienenee kahdella. Kahvaksi ei kelpaa
sivusaumaton lieriö, koska sen vaippaa ei voi mieltää tahkoksi, jonka
pitäisi olla monikulmio. Kahvan poistaminen palauttaa tilanteen ennalleen
eli E:n arvo kasvaa 2:lla.
Ilmeisesti jokainen kahvan liittäminen pudottaa E:n arvoa 2:lla ja
vastaavasti
jokainen kahvan poisto kasvattaa sitä 2:lla, joten yleisesti pätee
E(n-kahvainen pinta) = 2 - 2n.
Pinnat voidaan siis erotella luokkiin kahvamäärän perusteella ja luokka
selviää laskemalla tavalla tai toisella pinnan Euler-karakteristika.
Kriittinen lukija kysynee, miksi pitää nähdä näin paljon vaivaa
nähdäkseen, onko annettu pinta pallo vai rinkilä, kun asia selviää
katsomalla. Näin tietenkin onkin, kun on käytettävissä avaruuden kolmas
ulottuvuus ja voimme tarkastella pintaa ulkopuolelta. Mutta jos
olisimme toruksen pinnalla asuvia kaksiulotteisia olioita, joille
avaruuden kolmas ulottuvuus olisi tuntematon, emme voisi tarkkailla
maailmankaikkeuttamme ulkoapäin. Voisimme operoida vain pinnan sisällä.
Silloinkin, jos matematiikkaa harrastaisimme, päätyisimme käsitykseen
maailmankaikkeutemme luonteesta kolmioimalla asuinpintamme ja laskemalla
suureet T, S ja K. Laskelma T - S + K = 0 osoittaisi, että
maailmankaikkeutemme on rinkilän mallinen. Olemme 2-ulotteista
pintaa vaikeamman 3-ulotteisen avaruutemme kanssa periaatteessa samassa
asemassa kuin nuo kuvitellut 2-ulotteiset oliot. Emme voi tarkastella
3-ulotteisesta maailmaamme jostakin sen ulkopuolelta. Meidän on pystyttävä
selvittämään avaruutemme luonne avaruuden sisältä poistumatta. Tässä
2-ulotteisten pintojen tutkiminen saattaa antaa vihjeen oikeasta
lähestymistavasta.
Pintojen luokittelu kuuluu topologiaksi kutsuttuun matematiikan
alaan. Sen juuret juontavat 1700-luvulle, mutta pääosa topologiasta
on luotu kuluneella vuosisadalla. Lisää tietoa topologiasta saat jo
mainitusta Spectrum-tietokirjasta. Tutustu myös
topologian historiaan.
Solmu 2/1996-1997
Viimeksi muutettu: 11. toukokuuta 1997 klo 13:32:05
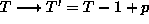
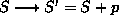
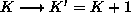
![[Torus]](torus.jpg)