Solmun tehtäväpalstalla julkaistaan koulukirjan tehtäviä
vaativampia ongelmia. Tehtävien lähde on yleensä jokin
matematiikkakilpailu, ja kilpailijoilla on ollut vain rajallinen aika
yrittää ratkaisua. Oikea matemaatikko ei suinkaan aina ratkaise
ongelmaansa ensi tapaamisella, vaan miettii kysymyksiään sitkeästi ja
eri aikoina. Jos otat ongelman miettiäksesi, älä hylkää sitä
heti, kun se alkaa tuntua ylivoimaiselta. Ratkaiseva idea voi tulla yön
nukkumisen jälkeen tai ensi viikolla.
Tällä kertaa tarjolla on tehtäviä runsaasti. Ratkaistavana
ovat 7. kansainvälisen Baltian tie -joukkuematematiikkakilpailun
tehtävät. Kilpailu pidettiin marraskuun alussa Päivölän kansanopistolla
Valkeakoskella, ja mukana oli viisihenkinen lukiolaisjoukkue Suomesta,
Ruotsista, Norjasta, Islannista, Tanskasta, Puolasta, Liettuasta, Latviasta,
Virosta ja Pietarista. Ratkaisuaikaa oli neljä ja puoli tuntia, ja kaikki
joukkueen viisi jäsentä tekivät yhteistä työtä. Kilpailun voitti
Puolan joukkue, joka sai ratkaistuksi 18 tehtävää oikein. Seuraavina
olivat Latvia ja Ruotsi; Suomi (Lauri Hallilla, Antti Honkela, Tuomo
Hyyryläinen, Peter Hästö ja Tomas Östman) oli kuudes.
Kokeile tehtäviä! Ne eivät ole mahdottomia. Jos onnistut
ratkaisemaan niitä, niin lähetä tuotoksesi minulle, joko tavallisessa
postissa osoitteeseen
Matti Lehtinen
Peukaloisentie 4 A 6
00820 Helsinki,
tai sähköpostiosoitteeseen
matti.lehtinen@helsinki.fi.
Parhaat ratkaisut julkaistaan seuraavassa Solmussa.
-
Olkoot
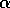 ja
ja 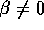 mitkä tahansa kaksi kulmaa,
joiden kyljet sisältävät säännöllisen 1996-kulmion lävistäjät.
Todista, että
mitkä tahansa kaksi kulmaa,
joiden kyljet sisältävät säännöllisen 1996-kulmion lävistäjät.
Todista, että 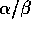 on rationaaliluku.
on rationaaliluku. -
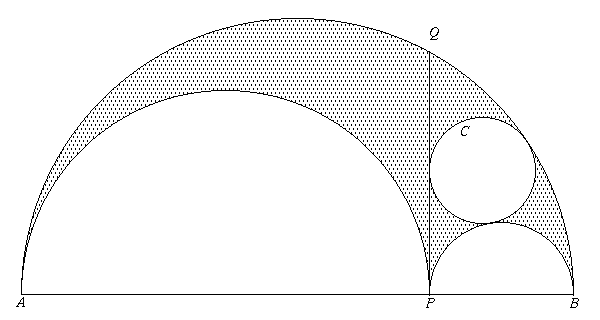
Alla olevan kuvan ympyrä C sivuaa kahta puoliympyrää ja janaa PQ,
joka on kohtisuorassa halkaisijaa AB vastaan.
Varjostetun alueen pinta-ala on
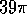 , ja ympyrän C ala on
, ja ympyrän C ala on 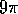 .
Laske halkaisijan AB pituus.
.
Laske halkaisijan AB pituus.
-
Olkoon ABCD yksikköneliö, ja olkoot P ja Q sellaisia
tason pisteitä, että Q on kolmion BPC ympäri piirretyn ympyrän
keskipiste ja D on kolmion PQA ympäri piirretyn ympyrän
keskipiste. Etsi kaikki janan PQ mahdolliset pituudet.
-
ABCD on puolisuunnikas (
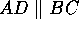 ). P on sellainen suoran
AB piste, että
). P on sellainen suoran
AB piste, että 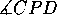 on suurin mahdollinen. Q on sellainen
piste suoran CD piste, että
on suurin mahdollinen. Q on sellainen
piste suoran CD piste, että 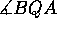 on suurin mahdollinen. Olettaen,
että P on janalla AB, osoita, että
on suurin mahdollinen. Olettaen,
että P on janalla AB, osoita, että 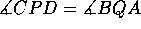 .
. -
Olkoon ABCD ympyrän sisään piirretty konveksi nelikulmio,
ja olkoot
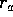 ,
, 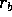 ,
,
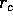 ,
, 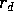 kolmioiden
BCD, ACD, ABD, ABC sisään piirrettyjen ympyröiden säteet.
Osoita, että
kolmioiden
BCD, ACD, ABD, ABC sisään piirrettyjen ympyröiden säteet.
Osoita, että
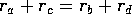 .
. -
Olkoot a,b,c,d sellaisia positiivisia kokonaislukuja, että ab=cd.
Osoita, että a+b+c+d ei ole alkuluku.
-
Kokonaislukujono
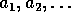 on sellainen, että
on sellainen, että 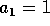 ,
,
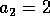 , ja kun
, ja kun 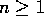 ,
,
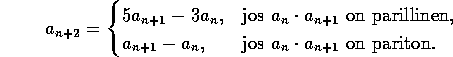
Osoita, että kaikilla n:n arvoilla 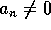 .
.
-
Tutkitaan jonoa
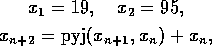
kun 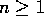 , missä
, missä 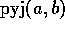 tarkoittaa a:n ja b:n pienintä
yhteistä monikertaa.
Etsi lukujen
tarkoittaa a:n ja b:n pienintä
yhteistä monikertaa.
Etsi lukujen 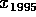 ja
ja 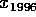 suurin yhteinen tekijä.
suurin yhteinen tekijä.
-
Olkoot n ja k kokonaislukuja,
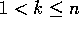 . Etsi joukko A,
joka koostuu n:stä kokonaisluvusta, ja kokonaisluku b, jotka
täyttävät seuraavat ehdot:
. Etsi joukko A,
joka koostuu n:stä kokonaisluvusta, ja kokonaisluku b, jotka
täyttävät seuraavat ehdot:
- Yksikään k-1:n A:n eri alkion tulo ei ole b:llä jaollinen.
- Jokainen k:n A:n eri alkion tulo on b:llä jaollinen.
- Jos a ja a' ovat A:n alkioita, a' ei ole a:lla jaollinen.
-
Merkitään d(n)llä positiivisen kokonaisluvun n erisuurten
positiivisten
tekijöiden lukumäärää (mukaan lukien 1 ja n). Olkoot a>1 ja n>0
sellaisia kokonaislukuja, että
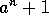 on alkuluku. Todista, että
on alkuluku. Todista, että

-
Reaaliluvuilla
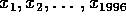 on seuraava
ominaisuus:
jos W on mikä tahansa
toisen asteen polynomi, ainakin kolme luvuista
on seuraava
ominaisuus:
jos W on mikä tahansa
toisen asteen polynomi, ainakin kolme luvuista
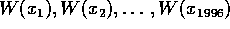 on yhtä suuria. Osoita, että ainakin kolme luvuista
on yhtä suuria. Osoita, että ainakin kolme luvuista
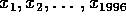 on yhtä suuria.
on yhtä suuria. -
Olkoon S kokonaislukujoukko, joka sisältää luvut 0 ja 1996.
Oletetaan myös, että S sisältää jokaisen sellaisen polynomin juuret,
jonka kertoimet sisältyvät S:ään ja joka ei ole identtisesti nolla.
Osoita, että S sisältää luvun -2.
-
Tarkastellaan kokonaislukujen joukossa määriteltyjä funktioita f,
jotka toteuttavat ehdon
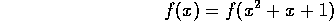
kaikilla kokonaisluvuilla x. Etsi kaikki tällaiset a) parilliset,
b) parittomat funktiot.
-
Funktion
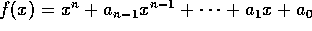 (missä n>1) kuvaaja leikkaa
suoran y=b pisteissä
(missä n>1) kuvaaja leikkaa
suoran y=b pisteissä 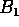 ,
, 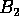 , ...,
, ..., 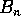 (vasemmalta
oikealle)
ja suoran y=c (
(vasemmalta
oikealle)
ja suoran y=c ( 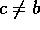 ) pisteissä
) pisteissä 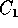 ,
, 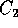 , ...,
, ..., 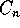 (vasemmalta oikealle).
Olkoon P suoran y=c piste, joka sijaitsee pisteen
(vasemmalta oikealle).
Olkoon P suoran y=c piste, joka sijaitsee pisteen 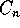 oikealla
puolella. Laske summan
oikealla
puolella. Laske summan
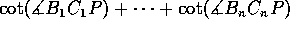 arvo.
arvo. -
Mille positiivisille reaaliluvuille a,b
pätee epäyhtälö
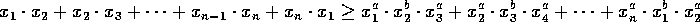
kaikille kokonaisluvuille n>2 ja kaikille positiivisille reaaliluvuille
 ?
?
-
Kaksi pelaajaa merkitsee vuorotellen äärettömän neliöruudukon
jo merkitsemättömiä ruutuja.
Toinen käyttää merkkiä
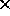 ,
toinen merkkiä
,
toinen merkkiä  .
Ensimmäinen, joka täyttää
.
Ensimmäinen, joka täyttää
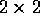 -neliön omilla merkeillään, voittaa.
Voiko aloittava pelaaja aina voittaa?
-neliön omilla merkeillään, voittaa.
Voiko aloittava pelaaja aina voittaa? -
Käyttäen kutakin kahdeksasta numerosta 1, 3, 4, 5, 6, 7,
8 ja 9 tasan kerran muodostetaan kolminumeroinen luku A,
kaksinumeroiset luvut B ja C (B<C) ja yksinumeroinen luku D.
Lisäksi pätee, että A+D=B+C=143. Monellako tavalla luvut voidaan
valita?
-
Olympialaisten tuomaristossa on 30 jäsentä. Tuomariston jokaisen
jäsenen mielestä osa hänen kollegoistaan on päteviä ja kaikki muut
epäpäteviä. Nämä mielipiteet eivät muutu. Jokaisen istunnon alussa
pidetään äänestys jokaisen jäsenen pätevyydestä. Sen jälkeen
tuomaristosta erotetaan sellaiset jäsenet, joita ei pidä pätevänä
aito enemmistö (yli puolet) äänestäjistä. Osoita, että korkeintaan
15 istunnon jälkeen tuomariston kokoonpano ei enää muutu. (Huomaa, että
kukaan ei äänestä omasta pätevyydestään.)
-
Neljässä kasassa on kussakin 38, 45, 61 ja 70 tulitikkua. Vuorollaan
pelaaja valitsee jotkin kaksi kasaa ja ottaa toisesta positiivisen
määrän tulitikkuja ja toisesta myös positiivisen määrän tulitikkuja.
Jos pelaaja ei voi tehdä siirtoa, hän häviää.
Kummalla pelaajista on voittostrategia?
-
Onko mahdollista jakaa positiiviset kokonaisluvut kahteen erilliseen
joukkoon A ja B, joille
- mitkään kolme A:n alkiota eivät muodosta
aritmeettista jonoa, ja
- B:n luvuista ei voida muodostaa kasvavaa ääretöntä
aritmeettista jonoa?
Kilpailun tulokset
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Yhteensä |
| Puola |
5 | 4 | 5 | 5 | 5 |
5 | 5 | 5 | 5 | 5 |
5 | 5 | 5 | 5 | 5 |
0 | 5 | 0 | 5 | 5 | 89 |
|---|
| Latvia |
5 | 3 | 5 | 5 | 0 |
5 | 5 | 5 | 5 | 2 |
5 | 5 | 4 | 5 | 3 |
5 | 5 | 0 | 5 | 5 | 82 |
|---|
| Ruotsi |
5 | 4 | 5 | - | - |
5 | 5 | 5 | 5 | 2 |
5 | - | 5 | 5 | 5 |
5 | 5 | 5 | 5 | 5 | 81 |
|---|
| Tanska |
4 | 5 | 5 | - | - |
5 | 5 | 5 | 5 | - |
5 | 5 | 5 | - | 3 |
5 | 5 | 3 | 5 | - | 70 |
|---|
| Pietari |
5 | - | 5 | 3 | - |
5 | 5 | 5 | 5 | 2 |
5 | 3 | 4 | 4 | - |
0 | 5 | 5 | 5 | 0 | 66 |
|---|
| Suomi |
5 | 5 | 5 | - | - |
- | 5 | 5 | 5 | 2 |
5 | 2 | 5 | 4 | 5 |
0 | 5 | - | 5 | - | 63 |
|---|
| Norja |
5 | 5 | 0 | - | 1 |
4 | 2 | - | 5 | - |
5 | 5 | 3 | 5 | 0 |
2 | 5 | 5 | 5 | 4 | 61 |
|---|
| Liettua |
5 | 1 | 5 | 0 | 0 |
4 | 5 | 5 | - | 2 |
5 | 2 | 5 | 1 | 5 |
- | 3 | 3 | 5 | 0 | 56 |
|---|
| Viro |
5 | 1 | 5 | - | - |
1 | 2 | 5 | 5 | 0 |
5 | 2 | 4 | - | - |
0 | 5 | 5 | 5 | 0 | 50 |
|---|
| Islanti |
3 | 5 | 5 | - | 1 |
0 | 5 | 0 | - | 2 |
- | - | 5 | 0 | - |
0 | 2 | 5 | 5 | 5 | 43 |
|---|
Matti Lehtinen

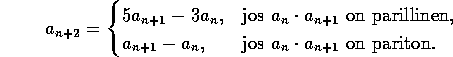
![]() .
.![]()
![]() , missä
, missä ![]() tarkoittaa a:n ja b:n pienintä
yhteistä monikertaa.
Etsi lukujen
tarkoittaa a:n ja b:n pienintä
yhteistä monikertaa.
Etsi lukujen ![]() ja
ja ![]() suurin yhteinen tekijä.
suurin yhteinen tekijä.![]()
![]()
![]()
![]() ?
?