PDF

Otsikkokuva

Solmun tehtävien ratkaisuja

Matti Lehtinen


Esitetään Solmun 1/2002 tehtävien 1-15 ratkaisut. Niitä on toimittajan lisäksi rustaillut Janne Mansikkamäki Vammalasta ja Pekka Aarnio Harjavallasta. Loput ratkaisut julkaistaan seuraavassa Solmussa.

1. Luku $(\sqrt {50}+7)^{2001}$ kehitetään desimaaliluvuksi. Määritä luvun 1. ja 2001. desimaali.

Ratkaisu. (Pekka Aarnio) Tunnetusti
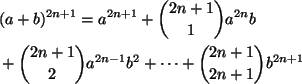
\begin{align*} &(a+b)^{2n+1}=a^{2n+1}+\binom{2n+1}{1}a^{2n}b\\ &+\binom{2n+1}{2}a^{2n-1}b^2 +\cdots+\binom{2n+1}{2n+1}b^{2n+1} \end{align*}
ja
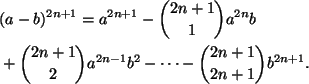
\begin{align*} &(a-b)^{2n+1}=a^{2n+1}-\binom{2n+1}{1}a^{2n}b\\ &+\binom{2n+1}{2}a^{2n-1}b^2 -\cdots-\binom{2n+1}{2n+1}b^{2n+1}. \end{align*}
Siten lausekkeissa $(\sqrt{50}+7)^{2n+1}$ ja $(\sqrt{50}-7)^{2n+1}$ on samat desimaaliosat, koska desimaaliosaa kertyy vain luvun $a=\sqrt{50}$ parittomista potensseista ja niillä on samat kertoimet ja etumerkit molemmissa lausekkeissa. Koska $\sqrt{50}-7=0{,}071\ldots<10^{-1}$, niin lausekkeessa $(\sqrt{50}-7)^{2001}$ on ainakin 2001 nollaa desimaaliosan alussa. Siten myös luvun $(\sqrt {50}+7)^{2001}$ desimaaliosassa on ainakin 2001 nollaa desimaalipilkun jälkeen. Kysytyt ensimmäinen ja 2001. desimaali ovat siis nollia kumpikin.

2. Kolmion sivujen pituudet ovat peräkkäisiä kokonaislukuja. Yksi kolmion keskijanoista on kohtisuorassa erästä kolmion kulmanpuolittajaa vastaan. Määritä kolmion sivujen pituudet.

Ratkaisu. Olkoot kolmion $ABC$ sivujen pituudet $a$, $b$ ja $c$. Voimme olettaa, että mediaani $AD$ ja kulman puolittaja $BE$ leikkaavat toisensa kohtisuorasti pisteessä $P$. Kolmiossa $BDA$ on silloin $BP$ sekä kulman puolittaja että korkeusjana. Kolmio $BDP$ on tasakylkinen. Mutta silloin $a=2c$. Koska $\{a,\,b,\,c\}$ on kolmen peräkkäisen kokonaisluvun joukko, $a-c$ on 1 tai 2. Jos $a-c=1$, $c=1$, $a=2$, jolloin $b=3$. Tällöin $ABC$ ei ole kolmio. On siis oltava $a-c=2c-c=2$, $c=2$, $a=4$, $b=3$.

3. Kuutio $K$ on leikattu $99$:ksi pienemmäksi kuutioksi. Näistä vain yhdellä särmän pituus ei ole 1. Määritä kuution $K$ tilavuus.

Ratkaisu. Jos alkuperäisen kuution särmä on $x$ ja $y\ne 1$ on osakuution särmä, niin $x$:n ja $y$:n on oltava muiden keskenään samankokoisten osakuutioiden särmän monikertoja eli $x$ ja $y$ ovat positiivisia kokonaislukuja. Lisäksi on oltava $x^3-y^3=98$ eli $(x-y)(x^2+xy+y^2)=98=2\cdot 7^2$. Koska $x-y<x^2+xy+y^2$, on oltava joko $x-y=1$ ja $x^2+xy+y^2=98$, $x-y=2$ ja $x^2+xy+y^2=49$ tai $x-y=7$, $x^2+xy+y^2=14$. Ensimmäinen vaihtoehto johtaa yhtälöön $(y+1)^2+y(y+1)+y^3=98$ eli $3(y^2+y)=97$. Koska 97 ei ole jaollinen 3:lla, tämä ei käy. Kolmas vaihtoehto puolestaan johtaa yhtälöön $(y+7)^2+y(y+7)+y^2=14$, mikä selvästikin on mahdotonta ($14<7^2$). Keskimmäinen vaihtoehto vuorostaan johtaa yhtälöön $y^2+4y+4+y^2+2y+y^2=3y^2+6y+4=49$ eli $y^2+2y-15=0$. Tämän yhtälön ainoa positiivinen ratkaisu on $y=3$. $x=5$ ja $y=3$ toteuttavat alkuperäisen yhtälön. Siis $x=5$, ja $K$:n tilavuus on 125 yksikköä.

4. Määritä suurin kokonaisluku $d$, joka on kaikkien lukujen $n(n+1)(2n+2002)$, missä $n$ on positiivinen kokonaisluku, tekijä.

Ratkaisu. Luvuista $n$ ja $n+1$ toinen on parillinen. Jos $n\equiv 2\mod 3$, niin $n+1$ on jaollinen 3:lla ja jos $n\equiv 1\mod 3$, niin $2n+2002\equiv 2004\equiv 0 \mod 3$. $n(n+1)(2n+2002)$ on siis aina jaollinen 12:lla. Tästä seuraa, että $d=12k$, missä $k$ on kokonaisluku. Jos $12k$ on tekijänä luvuissa $n(n+1)(2n+2002)$ ja $(n+1)(n+2)(2n+2004)$, se on tekijänä näiden lukujen erotuksessa, joka on $6(n+1)(n+668)$. $2k$ on siis tekijänä luvussa $(n+1)(n+668)$ kaikilla $n$ erityisesti $2k$ on tekijänä luvuissa $(2k+1)(2k+668)$ ja $(2k+2)(2k+669)$. Koska $2k$:lla ja $2k+1$:llä ei ole yhteisiä tekijä, se on $2k+668$:n tekijä. Mutta $2k+668$:lla ja $2k+669$:llä ei ole yhteisiä tekijöitä, joten $2k$ on $2k+2$:n tekijä. Silloin $2k$ on luvun 2 tekijä, joten $k=1$. Siis $d=12$.

5. Montako alkiota on suurimmassa joukon $A=\{1,\,2,\,\dots,\,547\}$ sellaisessa osajoukossa, jossa minkään kahden luvun summa ei ole jaollinen 42:lla?

Ratkaisu. Olkoon $A_i$ niiden $A$:n lukujen joukko, jotka ovat kongruentteja $i$:n kanssa modulo 42. Koska $547=13\cdot 42+1$, niin $A_1$:ssä on 14 alkiota ja muissa joukoissa $A_i$ on 13 alkiota. Jos $A$:n osajoukossa minkään kahden luvun summa ei ole jaollinen 42:lla, joukossa ei ole kahta lukua, joista toinen kuuluisi joukkoon $A_i$ ja toinen joukkoon $A_{42-i}$. Joukossa ei myöskään ole kahta lukua, jotka molemmat kuuluisivat joukkoon $A_0$ tai $A_{21}$. Maksimaalisessa ehdot täyttävässä osajoukossa voi siis olla joukot $A_1$, $A_2$, ..., $A_{20}$ ja yksi luku joukosta $A_0$ ja yksi luku joukosta $A_{21}$. Maksimaalinen alkiomäärä on $14+19\cdot 13+2=263$.

6. Ympyrät, joiden säteet ovat $h$ ja $k$, sivuavat suoraa $\ell$ pisteissä $A$ ja $B$. Ympyrät leikkaavat toisensa pisteissä $C$ ja $D$. Todista, että kolmioiden $ABC$ ja $ABD$ ympäri piirrettyjen ympyröiden säteet ovat samat. Määritä tämä säde.

Ratkaisu. Ratkaisu perustuu sinilauseen toistuvaan käyttöön. Voimme olettaa, että $D$ on kolmion $ABC$ sisäpiste. Kehäkulmalauseen perusteella $\angle CAB=180\as-\angle ADC$ ja $\angle ABC=180\as-\angle CDB$. Olkoon $R_C$ kolmion $ABC$ ympäri piirretyn ympyrän säde. Sinilauseen nojalla kolmioista $ADC$ ja $ABC$ saadaan $AC=2h\sin(\angle ADC)=2h\sin(\angle CAB)$ ja $AC=2R_C\sin(\angle ABC)$. Vastaavasti kolmioista $CDB$ ja $ABC$ saadaan $BC=2k\sin(\angle CDB)=2k\sin(\angle ABC)$ ja $BC=2R_C\sin(\angle CAB)$. Kun yhtälöt $2h\sin(\angle CAB)=2R_C\sin(\angle ABC)$ ja $2k\sin(\angle ABC)=2R_C\sin(\angle CAB)$ kerrotaan keskenään, saadaan $R_C^2=hk$. Olkoon $R_D$ kolmion $ABD$ ympäri piirretyn ympyrän säde. Nyt $\angle DAB=\angle DCA$ ja $\angle ABD=\angle BCD$. Kolmioista $ADC$ ja $ABD$ saadaan $AD=2h\sin(\angle DCA=2h\sin(\angle DAC)=2R_D\sin(\angle ABD)$, kolmioista $DBC$ ja $ABD$ puolestaan $DB=2k\sin(\angle BCD)=2k\sin(\angle ABD)=2R_D\sin(\angle DAB)$. Kun yhtälöt kerrotaan keskenään, saadaan $R_D^2=hk$. Säteet $R_C$ ja $R_D$ ovat samat ja $=\sqrt{hk}$.

7. Olkoon positiivisten lukujen $a_1$, $a_2$, ..., $a_n$ tulo 1. Osoita, että

\begin{displaymath} \sqrt {a_1}+\sqrt {a_2}+\cdots+\sqrt {a_n}\leqslant a_1+a_2+\cdots+a_n. \end{displaymath}

Ratkaisu. Aritmeettis-geometrisen epäyhtälön nojalla
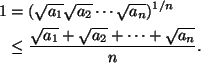
\begin{align*} 1&=(\sqrt{a_1}\sqrt {a_2}\cdots\sqrt {a_n})^{1/n}\\ &\le \frac{\sqrt {a_1}+\sqrt{a_2}+\cdots+\sqrt {a_n}}{n}. \end{align*}
Cauchy-Schwarzin epäyhtälön nojalla
\begin{align*} &(\sqrt {a_1}+\sqrt {a_2}+\cdots+\sqrt {a_n})^2\le n(a_1+a_2+\cdo... ...le(\sqrt {a_1}+\sqrt {a_2}+\cdots+\sqrt{a_n})(a_1+a_2+\cdots a_n). \end{align*}
Väite saadaan tästä jakolaskulla.

8. Seurueen jokaisen neljän jäsenen joukossa on yksi, joka on tuttu kyseisten kolmen muun jäsenen kanssa. Todista, että seurueessa on ainakin yksi jäsen, joka on tuttu seurueen kaikkien muiden jäsenten kanssa.

Ratkaisu. Oletetaan, että seurueessa kukaan ei tunne kaikkia muita. Olkoon $A$ eräs seurueen jäsen. Seurueessa on silloin ainakin yksi jäsen $B$, joka ei ole tuttu $A$:lle. Olkoot $C$ ja $D$ kaksi muuta seurueen jäsentä. Joukossa $\{A,\,B,\,C,\,D\}$ on ainakin yksi, joka tuntee muut kolme. Tämä yksi ei ole $A$ eikä $B$, joten se on $C$ tai $D$. Joka tapauksessa $C$ ja $D$ tuntevat toisensa. Koska $C$ ja $D$ ovat mielivaltaisia, tiedetään, että jos $A$ ja $B$ poistetaan seurueesta, kaikki muuta jäsenet tuntevat toisensa. Mutta joko $C$ tai $D$ tunsi sekä $A$:n että $B$:n ja niin muodoin kaikki seurueen jäsenet. Ristiriita, joka osoittaa alkuperäisen oletuksen virheelliseksi.

9. Varastossa on 2001 juustonpalaa. Todista, että on mahdollista leikata yksi paloista kahteen osaan niin, että palat voidaan kerätä kahteen säkkiin, joiden sisältö painaa yhtä paljon ja joissa on kummassakin yhtä monta palaa.

Ratkaisu 1. Olkoot juustonpalojen painot $a_1\le a_2\le \dots\le a_{2001}$. Valitaan palat $a_1$, $a_3$, ..., $a_{1999}$ toiseen säkkiin ja palat $a_2$, $a_4$, ..., $a_{2000}$ toiseen. Säkkien painon erotus on
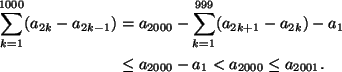
\begin{align*} \sum_{k=1}^{1000}(a_{2k}-a_{2k-1})&=a_{2000}- \sum_{k=1}^{999}(a_{2k+1}-a_{2k})-a_1\\ &\le a_{2000}-a_1<a_{2000}\le a_{2001}. \end{align*}
Mutta näin ollen pala $a_{2001}$ voidaan leikata kahdeksi palaksi, joiden painojen erotus on sama kuin säkkien painojen erotus. Kun raskaampi pala pannaan kevyempään säkkiin ja kevyempi raskaaseen, molemmat säkit tulevat yhtä painaviksi.

Ratkaisu 2. (Janne Mansikkamäki) Todistetaan induktiolla, että $2n-1$ juustonpalaa voidaan aina säkittää vaaditulla tavalla.

$1^\circ$. Kun $n=1$, paloja on yksi, ja se voidaan jakaa kahdeksi yhtä suureksi palaksi.

$2^\circ$. Oletetaan, että kun $n=k$, jako voidaan tehdä. Olkoon sitten $n=k+1$. Jaetaan ensin $2k-1$ palaa tehtävän mukaisesti kahteen säkkiin. Tällöin on yksi paloista jaettu kahdeksi osaksi. Olkoon sen paino $x_1$. Kun tämän palan osat poistetaan säkeistä, niissä on yhä yhtä monta palaa. Säkit painavat $s_1$ ja $s_2$. Oletetaan, että $s_1\le s_2$. Huomataan, että $s_2-s_1< x_1$. Nyt säkkeihin on laittamatta kolme palaa. Niiden painot ovat $x_1$, $x_2$ ja $x_3$. Voidaan olettaa, että $x_1\le x_2\le x_3$. Jaetaan nyt suurin pala osiksi, joiden painot ovat $d$ ja $x_3-d$. 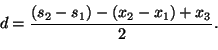Osoitetaan, että $d$ voidaan valita niin, että \begin{equation*} s_1+x_2+d=s_2+x_1+(x_3-d) \end{equation*} eli \begin{equation*} d=\frac{(s_2-s_1)-(x_2-x_1)+x_3}{2}. \end{equation*} Koska $s_2-s_1\le x_1$ ja $x_2-x_1\le x_2$, niin $\vert(s_2-s_1)-(x_2-x_1)\vert< x_2\le x_3$, joten todellakin $d<x_3$. Induktioaskel voidaan siis ottaa.

10. Kokonaislukukertoimisella $n$:nnen asteen ($n\geqslant 5$) polynomilla $P(x)$ on $n$ eri kokonaislukunollakohtaa $0$, $x_2$, $x_3$, ..., $x_n$. Määritä polynomin $P(P(x))$ kokonaislukunollakohdat.

Ratkaisu. Tehtävän mukaan $P(x)=a_nx(x-x_2)(x-x_3)\cdots(x-x_n)$, missä $a_n$ on kokonaisluku. Osoitetaan, että $P(k)\ne x_i$ kaikilla $i\ge 2$ ja kaikilla kokonaisluvuilla $k$. Vastaoletukseksi voidaan asettaa $P(k)=x_2$ jollain kokonaisluvulla $k$. Silloin $k$ on $x_2$:n tekijä, eli $x_2=kt$ jollain kokonaisluvulla $t$. Edelleen silloin $a_nk(1-t)(k- x_3)\cdots(k-x_n)=t$, joten $1-t$ on $t$:n tekijä. Silloin joko $t=0$ tai $t=2$. Jos $t=0$, $x_2=0$, mikä ei ole tehtävän ehtojen mukaan mahdollista. Siis $t=2$ ja $a_nk(k-x_3)(k- x_4)\cdots(k-x_n)=-2$. Luvut $k$, $k-x_3$, $k-x_4$, ..., $k- x_n$ ovat kaikki eri lukuja ja luvun $-2$ tekijöitä. Koska viimeinen ehto toteutuu vain, kun luvut kuuluvat joukkoon $\{- 2,\,-1,\,1,\,2\}$, on oltava $n=5$ ja $\vert a_nk(k-x_3)(k-x_4)(k- x_5)\vert\ge 4$. Ristiriita. Siis $P(x)\ne x_i$, joten $P(P(x))=0$ vain, kun $P(x)=0$ eli $x$ on jokin $P$:n nollakohdista $0$, $x_i$.

11. Veljekset möivät $n$ lammasta hintaan $n$ euroa/lammas. Rahat jaettiin niin, että vanhempi veli otti ensin 10 euroa, sitten nuorempi otti 10 euroa jne., kunnes oli nuoremman veljen vuoro ottaa rahaa, jota ei kuitenkaan enää ollut kymmentä euroa. Tällöin sovittiin, että nuorempi veli saa loput rahat sekä vanhemman linkkuveitsen, ja jako menee tasan. Minkä arvoinen oli linkkuveitsi?

Ratkaisu. Veljekset saivat $n^2$ dollaria. Olkoon $n=10a+b$. Silloin $n^2=100a^2+20ab+b^2$. Kertomuksen mukaan $n^2=(2k+1)\cdot 10+y$. Luvun $b^2$ on oltava muotoa $(2m+1)\cdot 10+y$. Mutta kymmentä pienempien lukujen neliöistä tätä muotoa ovat vain 16 ja 36. Koska viimeisessä jakovaiheessa vanhempi veli sai 10 dollaria ja nuorempi siis 6, täytyy linkkuveitsen arvon olla 2 dollaria.

12. Reaaliluvut $a$ ja $b$ toteuttavat yhtälöt

\begin{displaymath} a^3-3ab^2=20,\quad b^3- 3a^2b=40. \end{displaymath}

Määritä $a^2+b^2$.

Ratkaisu.
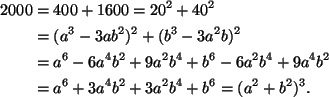
\begin{align*} 2000&=400+1600=20^2+40^2\\ &= (a^3-3ab^2)^2+(b^3-3a^2b)^2\\ &=a... ...^2b^4+b^6-6a^2b^4+9a^4b^2\\ &=a^6+3a^4b^2+3a^2b^4+b^6=(a^2+b^2)^3. \end{align*}
Siis $a^2+b^2=\root 3\of{2000}$.

13. Olkoon

\begin{displaymath} a_n=\left\lfloor\frac{n}{1}\right\rfloor +\left\lfloor\frac{n}{2} \right\rfloor +\cdots+\left\lfloor\frac{n}{n}\right\rfloor. \end{displaymath}

Osoita, että $a_n=2+a_{n-1}$ silloin ja vain silloin, kun $n$ on alkuluku.

Ratkaisu. Kirjoitetaan yhtälö $a_n=2+a_{n-1}$ muotoon
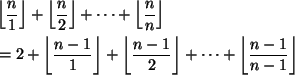
\begin{align*} &\left\lfloor\frac{n}{1}\right\rfloor +\left\lfloor\frac{n}{2} \r... ...}{2}\right\rfloor +\cdots+\left\lfloor \frac{n-1}{n-1}\right\rfloor \end{align*}
eli
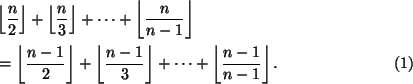
\begin{align*} &\left\lfloor\frac{n}{2}\right\rfloor +\left\lfloor\frac{n}{3} \r... ...t\rfloor +\cdots+\left\lfloor \frac{n-1}{n-1}\right\rfloor.\tag{1} \end{align*}
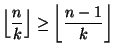Selvästi kaikilla $k$, $2\le k\le n-1$ on $\left\lfloor \dfrac{n}{k}\right\rfloor\ge \left\lfloor\dfrac{n-1}{k} \right\rfloor$, joten
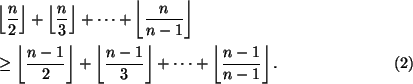
\begin{align*} &\left\lfloor\frac{n}{2}\right\rfloor +\left\lfloor\frac{n}{3}\ri... ...ht\rfloor +\cdots+\left\lfloor \frac{n-1}{n-1}\right\rfloor.\tag{2} \end{align*}
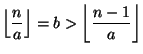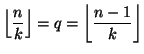Jos $n=ab$, $2\le a<n$, niin $\left\lfloor\dfrac{n}{a}\right\rfloor =b>\left\lfloor\dfrac{n-1}{a}\right\rfloor$. Tällöin (2):ssa on aito erisuuruus, joten (1) ei toteudu. Mutta jos $n$ on alkuluku, on kaikilla $k$ $n=qk+r$, missä $1\le r<k$. Silloin kaikilla $k$ on $\left\lfloor\dfrac{n}{k}\right\rfloor=q=\left\lfloor\dfrac{n-1}{k} \right\rfloor$, ja (1) toteutuu.

14. Todista, että kaikilla luonnollisilla luvuilla $n$ luku $2^n+n^2$ on jaollinen 5:llä silloin ja vain silloin, kuin luku $n^2\cdot 2^n+1$ on jaollinen 5:llä.

Ratkaisu. Jos $n=5k$, niin kumpikaan luvuista $2^n+n^2$ ja $n^2\cdot 2^n+1$ ei ole jaollinen 5:llä. Jos $n=5k\pm 1$, niin $(n- 1)(n+1)=n^2-1$ on jaollinen 5:llä. Koska $n^22^n+1=(2^n-1)(n^2- 1)+2^n+n^2$, ja $n^22^n+1$ ja $2^n+n^2$ ovat samanaikaisesti 5:llä jaollisia. Jos $n=5k\pm 2$, $n^2+1=25k^2\pm 20k+4+1$, joten $n^2+1$ on jaollinen 5:llä. Mutta $n^22^n+1=(2^n+1)(n^2+1)-2^n-n^2$, ja $n^22^n+1$ ja $2^n+n^2$ ovat jälleen samanaikaisesti 5:llä jaollisia.

15. Määritä kaikki alkuluvut $n$, joiden kymmenjärjestelmäesitys on $n=10101\dots 01$.

Ratkaisu. Tehtävän luvut ovat muotoa 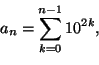\begin{equation*} a_n=\sum_{k=0}^{n-1}10^{2k}, \end{equation*} missä $n\ge 2$ on luvussa olevien ykkösten määrä. Jos $n$ on parillinen, $a_n$ on jaollinen 101:llä. 101 on itsessään alkuluku. Jos $n=2p+1$, niin
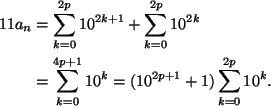
\begin{align*} 11a_n&=\sum_{k=0}^{2p}10^{2k+1}+\sum_{k=0}^{2p}10^{2k}\\ &=\sum_{k=0}^{4p+1}10^k =(10^{2p+1}+1)\sum_{k=0}^{2p}10^k. \end{align*}
Jos $p\ge 1$, niin oikean puolen molemmat tekijät ovat $>11$, joten $a_n$ ei voi olla alkuluku. Siis 101 on ainoa vaadittua muotoa oleva alkuluku.

Solmun toimitus
11.6.2002