PDF

Otsikkokuva

Onko ympyrä aina pyöreä?

Timo Tossavainen
Lehtori
Savonlinnan opettajankoulutuslaitos, Joensuun yliopisto


Varsin usein matemaattisen ongelman ratkaisun löytyminen on kiinni siitä, kykenemmekö mielemme silmin näkemään ongelmaan liittyvät käsitteet ja näiden väliset suhteet jonkinlaisena kuvana. Käytännössä pyrimme siis luomaan mielikuvituksemme avulla geometrisen mallin ongelmasta ja katselemalla tätä mallia yritämme löytää ratkaisun. Tällöin on ensisijaisen tärkeää kiinnittää huomiota siihen, miksi ja millä tavalla mallimme vastaa käsitteitä ja ennen kaikkea, voidaanko samoista käsitteistä laatia useita erinäköisiä malleja.

Jos meitä pyydetään ajattelemaan ympyrää tai piirtämään siitä paperille kuva, tuskinpa monellekaan tulee mieleen muuta kuin sellainen pyöreämuotoinen suljettu viiva, joka voidaan ainakin periaatteessa piirtää siten, että ensin kiinnitetään narunpätkän toiseen päähän kynä, pidetään narun toista päätä paikoillaan ja sitten pyöräytetään kireänä pidettyä narua kiinnitetyn pään ympäri. Tällaisessa tempussa oleellista on, että liikkuva kynänterä pysyy vakioetäisyyden päässä kiinnitetystä pisteestä eli piirtyvän ympyrän keskipisteestä.

Edellä kuvatussa tempussa narun rooli on toimia jonkinlaisena etäisyyden säätimenä, ja jos etäisyys todella pysyy vakiona pyöräytyksen ajan, syntyy kuvio, joka vastaa sitä, mitä sanalla ympyrä matematiikassa yleensä tarkoitetaan: $O$-keskinen ja $r$-säteinen ympyrä on tason niiden pisteiden ura, joiden etäisyys pisteestä $O$ on tasan $r$.

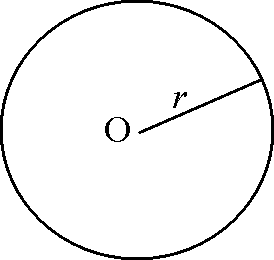
Kuva 1

Tämä määritelmä tuntuu hyvin selkeältä ja yksikäsitteiseltä, mutta tarkka lukija voi huomata, että ainakin kahden asian kohdalla voidaan hieman spekuloida. Ensinnäkin, millainen pinta kelpaa piirtämistasoksi? Jos piirrämme narun ja kynän avulla ympyrän reikäiselle taivutetulle paperille tai vaikkapa puhalletun Mikki Hiiri -ilmapallon pinnalle, kuva ympyrästä voi olla erilainen kuin taivuttamattomalle ehjälle paperille piirretty kuva. Me emme kuitenkaan puutu tässä esityksessä kysymykseen piirtämistasosta, vaan ajattelemme tason olevan ehjän ja taivuttamattoman (hyvin ison) paperin kaltainen. Sen sijaan mietimme tarkemmin sitä, mitä pisteiden välisen etäisyyden mittaamisella oikein tarkoitetaan.

Pythagoraan lauseeseen perustuva laskukaava

\begin{displaymath} d(P,Q)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \leqno(1) \end{displaymath}

on luonnollinen valinta kahden koordinaattipisteen $P=(x_1,y_1)$ ja $Q=(x_2,y_2)$ välisen matkan mittaamiseen sellaisessa tasossa, jossa mikään liikkumisen suunta ei ole estetty tai hankampi kuin mikä tahansa muu suunta. Tätä mittaamistapaa vastaa luonnossa - ainakin lyhyehköillä matkoilla - ns. linnuntie. Kuitenkin meidän normaalisti maata pitkin liikkuvien olentojen yleinen kokemuksemme on, ettemme esimerkiksi suurkaupungin ruutukaava-alueella pysty liikkumaan kahden kohteen välillä mitä tahansa reittiä pitkin, vaan meidän on kuljettava toisiinsa nähden enemmän tai vähemmän samansuuntaisia tai kohtisuoria katuja pitkin. Tällöin herää kysymys mikä on oikea tai luonnollisin tapa mitata pisteiden välisiä etäisyyksiä tasoissa (tai yleisemmin avaruuksissa), joissa liikkumisen hankaluus on suuntariippuvaista.

Kuva 2

Ennen kuin etsimme oikean laskukaavan ruutukaavatason pisteiden välisen etäisyyden laskemiseksi, on meidän parasta ensin pohtia mitä kunnolliselta etäisyyden mittaamiselta yleensä voi ja kannattaa vaatia. Eräs tällainen vaatimus on se, että käytetäänpä etäisyyden mittaamiseen mitä tahansa mittaria, matka mistään pisteestä itseensä ei saa olla muuta kuin nolla. Toisaalta on luontevaa odottaa, että kahden pisteen välinen etäisyys on aina positiivinen luku. Lisäksi kannattaa vaatia, että pisteiden välinen etäisyys on riippumaton siitä, mitataanko matka pisteestä $P$ pisteeseen $Q$ vai päinvastoin. Tietenkin myös se on toivottavaa, että tutkittavana olevan avaruuden jokaisen pisteparin välinen etäisyys saadaan yksikäsitteisellä tavalla mitatuksi.

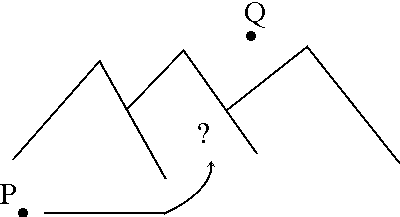
Oikeastaan jokainen etäisyysmittari, joka toteuttaa edellä kuvatut vaatimukset, on käyttökelpoinen ainakin matematiikan maailmassa, mutta reaalimaailman kokemustemme pohjalta olemme kiinnostuneita erityisesti sellaisista etäisyysmittareista, jotka lisäksi toimivat siten, etteivät ne koskaan anna kahden pisteen väliseksi etäisyydeksi suoraan mitattuna suurempaa lukua kuin mutkan eli minkä tahansa kolmannen pisteen kautta mitattuna. Kutsumme tässä esityksessä tällaista etäisyysmittaria kunnolliseksi.

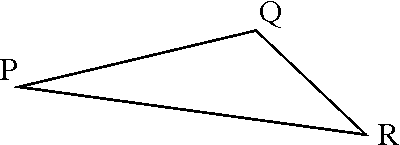
Kuva 3

Voimme ilmaista myös matematiikan kielellä millainen objekti tason (tai yleisemmin avaruuden) kunnollinen etäisyysmittari on. Tason pisteparien joukolta positiivisille reaaliluvuille määritelty funktio $\delta$ on kunnollinen tason etäisyysmittari, jos sillä on seuraavat ominaisuudet:

(i)
$\delta(P,Q)=0$, jos ja vain jos $P=Q$,
(ii)
$\delta(P,Q)\ge 0$ kaikilla $P$ ja $Q$,
(iii)
$\delta(P,Q)=\delta(Q,P)$ kaikilla $P$ ja $Q$,
(iv)
$\delta(P,R)\le \delta(P,Q)+\delta(Q,R)$ kaikilla $P$, $Q$ ja $R$.
Jokaista funktiota $\delta$, joka toteuttaa ehdot (i)-(iv), sanotaan metriikaksi.

On helpohko laskutehtävä osoittaa, että kohdan (1) luonnollisen etäisyyden laskukaava toteuttaa metriikan vaatimukset. Mutta on olemassa myös muita funktioita, jotka toteuttavat samat vaatimukset. Esimerkiksi kaavan

\begin{displaymath}d_1(P,Q)=\vert x_1-x_2\vert+\vert y_1-y_2\vert,\leqno(2)\end{displaymath}

missä $P=(x_1,y_1)$ ja $Q=(x_2,y_2)$, avulla tason pisteparien joukossa määritelty funktio $d_1$ toteuttaa nämä vaatimukset. Väite seuraa siitä, että reaalilukujen itseisarvolla on seuraavat ominaisuudet: $\vert a\vert=0$, jos ja vain jos $a=0$, ja muuten $\vert a\vert>0$. Toisaalta, kaikilla $a,b,c\in\Bbb R$ on $\vert a-b\vert=\vert b-a\vert$ ja

\begin{displaymath}\vert a-c\vert=\vert(a-b)+(b-c)\vert\le \vert a-b\vert+\vert b-c\vert.\end{displaymath}

Jos katsomme tarkemmin kohdan (2) kaavaa, huomaamme, että $d_1$ ilmoittaa tason pisteiden välisen matkan pitkin koordinaattiakseleiden suuntaisia suoria. Tämä vastaa hyvin liikkumista ruutukaava-alueella, joten $d_1$ on luonnollinen etäisyysmittari ainakin Manhattanilla asuville. Itse asiassa tasoa varustettuna metriikalla $d_1$ sanotaankin usein taksiautotasoksi.

Taksiautotasolla on monia mielenkiintoisia ominaisuuksia, jotka erottavat sen tavallisesta koulugeometrian tasosta. Huomaamme, että jos pisteillä $P$ ja $Q$ molemmat koordinaatit eroavat toisistaan, lyhin reitti näiden kahden pisteen välillä ei olekaan enää yksikäsitteisellä tavalla määräytyvä. Seuraavaan kuvaan on piirretty kaksi mahdollista yhtä pitkää (lyhintä) reittiä $(a)$ ja $(b)$ taksiautotason pisteiden $P$ ja $Q$ välille.

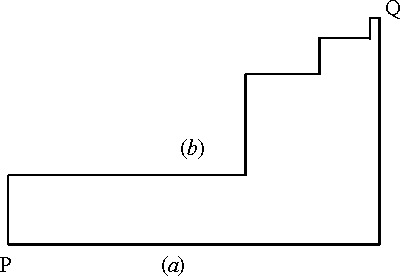
Kuva 4

Millaisia ovat ympyrät taksiautotasossa? Koska pisteiden välinen etäisyys mitataan pitkin koordinaattiakseleiden suuntaisia suoria, saadaan origokeskisen $r$-säteisen ympyrän kuvaksi salmiakkiruutu, jonka kärjet ovat pisteissä $(\pm r, 0)$ ja $(0,\pm r)$.

On siis mahdollista laatia kunnollisen etäisyysmittarin avulla myös sellaisia malleja, joissa ympyrät ovat kulmikkaita. Nokkela lukija keksii pian kuinka metriikkaa $d_1$ pitää muokata, jotta hän saisi toisen metriikan, jonka määräämät ympyrät näyttävät neliöiltä, joiden sivut ovat koordinaattiakseleiden suuntaiset.

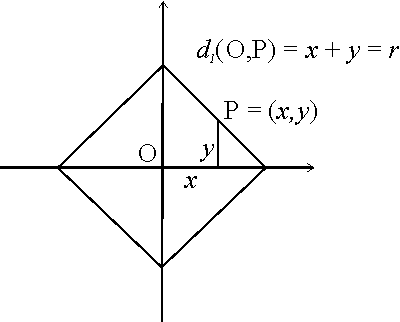
Kuva 5

Tasoon voidaan määritellä myös epäjatkuva metriikka. Esimerkiksi tason pisteparien joukossa määritelty kuvaus $d_0$, jolle

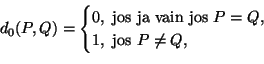
\begin{displaymath} d_0(P,Q)= \begin{cases} 0, \text{ jos ja vain jos } P=Q, \\ 1, \text{ jos }P\ne Q, \end{cases}\end{displaymath}

on metriikka. Nimittäin, $d_0$ selvästi toteuttaa metriikan ehdot (i)-(iii). Lisäksi ehto (iv) toteutuu, sillä jos $P=R$, niin

\begin{displaymath}0=d_0(P,R)\le d_0(P,Q)+d_0(Q,R),\end{displaymath}

ja jos $P\ne R$, niin $Q\ne P$ tai $Q\ne R$ ja näin ollen

\begin{displaymath}d_0(P,Q)+d_0(Q,R)\ge 1.\end{displaymath}

Jos käytämme metriikkaa $d_0$ etäisyysmittarina, niin mikä tahansa piste keskipisteenä piirretty 1-säteinen ympyrä peittää koko tason paitsi ei kyseisen ympyrän keskipistettä. Toisaalta, metriikalla $d_0$ varustetussa tasossa ei ole olemassa $r$-säteisiä ympyröitä, jos $r\ne 1$.

Tasoon voidaan määritellä äärettömän monta eri metriikkaa, sillä esimerkiksi kertomalla kaavan (1) juurilauseke jollakin vakiolla saadaan uusi funktio, joka on metriikka. Toisaalta tason kahden metriikan summafunktio on aina tason metriikka. Näin ollen on mahdollista laatia lukemattomia erilaisia malleja, joissa ympyrät voivat kuvioina poiketa toisistaan oleellisesti, vaikka jokaisessa mallissa ympyrän määritelmä sinänsä on sama.

Metriikkojen ja niiden avaruuksien, joissa voidaan määritellä erilaisia metriikkoja, tarkastelu kuuluu siihen matematiikan alaan, jota sanotaan topologiaksi. Matematiikan historiassa topologia on varsin uusi asia, sillä sen katsotaan saaneen alkunsa kuuluisasta Königsbergin siltaongelmasta, jonka Euler ratkaisi 1700-luvulla. Topologian alkeista on kirjoitettu joitakin hyviä oppikirjoja myös suomenkielellä.

Sivuhuomatus maailmankaikkeuden mittaamisesta

Jokaisen sukupolven edustajat lienevät pohtineet sitä, onko maailmankaikkeus ihan oikeasti äärellinen vai ääretön. Erilaisten metriikkojen tarkastelu voi johtaa meidät tässä kysymyksessä mielenkiintoisen (ainakin osittaisen) vastauksen äärelle.

Olkoon $d$ tason luonnollisen metriikan vastine avaruudessa. Määritellään avaruuden pisteparien joukossa funktio $d^*$ seuraavan kaavan avulla:

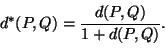
\begin{displaymath} d^*(P,Q)=\frac{d(P,Q)}{1+ d(P,Q)}. \end{displaymath}

Välittömästi nähdään, että $d^*$ toteuttaa metriikan vaatimuksista ainakin kohdat (i)-(iii). Pienehkön laskutehtävän jälkeen huomaamme, että $d^*$ täyttää myös neljännen vaatimuksen. Erikoista tässä metriikassa kuitenkin on se, että sen arvot ovat aina nollan ja yhden väliltä.

On siis mahdollista mitata samaa avaruutta arvoiltaan sekä rajoittamattomilla että rajoitetuilla etäisyysmittareilla. Koska mittarit ovat ominaisuuksiltaan muuten samanlaisia, emme voi asettaa kumpaakaan mittaamistapaa sinänsä toista oikeammaksi. Näin ollen ei ole mielekästä ottaa ehdotonta kantaa siihen, onko maailmankaikkeutemme objektiivisesti pieni vai suuri ns. ulkopuolisen tarkkailijan silmin, sillä emme voi tietää, mittaako tämä hypoteettis-spekulatiivinen hahmo maailmaamme rajoitetulla vai rajoittamattomalla mittarilla.


Matematiikkalehti Solmu
6.3.2002