PDF

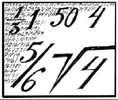
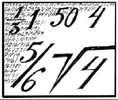
Otsikkokuva

Descartesin merkillinen sääntö

Matti Lehtinen

Historia tuntee René Descartesin (1596-1650) sinä filosofina, joka totesi cogito, ergo sum, ajattelen, olen siis olemassa, ja rakensi tästä vastaansanomattomasta totuudesta lähtien rationaalisen filosofian järjestelmän. Huomionarvoista on myös, että Descartes ei arvostanut aikaista ylösnousua. Hän arveli saaneensa kaikki merkittävät ajatuksensa aamupäivisin sängyssä loikoillessaan. Matemaatikoille Descartes eli Cartesius on arkipäivää suorakulmaisen, karteesisen koordinaatiston ja joukkojen karteesisen tulon myötä.

Descartes ei tiettävästi koskaan esittänyt tai käyttänyt suorakulmaista $xy$-koordinaatistoa, vaikka hänen matemaattista pääteostaan La Géométrie syystä pidetään analyyttisen geometrian perustajana. Samasta kirjasta on peräisin myös tämän kirjoituksen aihe, Descartesin merkkisääntö. Suppea kysely osoitti, että tämä sääntö ei ole kovin monelle tuttu.

Descartesin merkkisääntö koskee yhtä matematiikan keskeisimmistä ongelmista, polynomiyhtälön ratkaisemista. $n$:nnen asteen yhtälö voidaan aina kirjoittaa muotoon

\begin{displaymath}P(x)=x^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0=0.\eqno(1)\end{displaymath}

Jos $n=1$ tai $n=2$, yhtälön ratkaisu on hyvin tunnettu, ja jos $n=3$ tai $n=4$, ratkaisu voidaan, joskin työläästi, aina löytää. Mutta yleisessä tapauksessa ei pelkästään yhtälöä katsomalla usein edes pysty sanomaan, toteutuuko yhtälö millään reaaliluvulla saati kertomaan, millä $x$:n arvoilla yhtälö ehkä toteutuu. Descartesin sääntö ei sekään kerro yhtälön ratkaisuja edes likimäärin. Mutta se antaa hyvin yksinkertaisen keinon, jonka avulla voi päätellä jotain yhtälön ratkaisuista.

Yhtälön (1) polynomin kertoimet muodostavat reaalilukujonon $(1,\,a_{n- 1}$, $a_{n-2}$, ..., $a_0)$. Jonon luvuista osa voi olla nollia. Unohdetaan ne. Loput ovat joko positiivisia tai negatiivisia. Täten yhtälöön liittyy yksikäsitteinen symbolien $+$ ja $-$ jono:

\begin{displaymath}(+,\,\pm,\,\pm,\,\dots,\,\pm).\eqno(2)\end{displaymath}

Descartesin merkkisääntö sanoo, että yhtälöllä (1) on enintään niin monta positiivista ratkaisua, kuin jonossa (2) on merkin vaihtoja, siis $(+,\,-)$ tai $(-,\,+)$ -tyyppisiä kohtia. Jos kaikki kertoimet $a_k$ ovat nollasta eroavia, niin negatiivisia ratkaisuja on enintään niin monta kuin jonossa (2) on peräkkäisiä samoja merkkejä, siis tyyppiä $(+,\,+)$ tai $(-,\,-)$ olevia kohtia.

Descartes antaa esimerkiksi yhtälön

\begin{displaymath}x^4-4x^3-19x^2+106x-120=0.\end{displaymath}

Sen merkkijono on $(+,\,-,\,-,\,+,\,-)$. Merkinvaihtoja on kolme ja yksi merkin säilyminen. Yhtälöllä onkin kolme positiivista ratkaisua: 2, 3 ja 4, ja yksi negatiivinen ratkaisu, $x=-5$. Descartes muuten kutsui yhtälön negatiivisia ratkaisuja vääriksi.

Jotkin säännön erikoistapaukset ovat selviä. Jos kertoimet $a_k$ ovat positiivisia, ei yhtään positiivista juurta voi olla. Jos kertoimet $a_{n- 1}$, $a_{n-2}$, ..., $a_1$, $a_0$ ovat kaikki negatiivisia, merkinvaihtoja on 1. Tällöin myös $P(0)=a_0<0$, mutta $P(x)\to \infty$, kun $x\to \infty$. Nollakohtia on oltava ainakin yksi. Mutta merkkisäännön mukaan niitä ei voi olla myöskään enempää. Siis niitä on tasan yksi.

Yleisessä tapauksessa Descartesin sääntö tarvitsee perustelun. Sitä ei kannata etsiä Descartesin teoksesta, koska tämä kertoo sääntönsä vain faktana, ilman todistusta. Mutta onneksi meillä on käytössä keino, jota Descartesilla ei vielä ollut: differentiaalilaskenta. Hyötyä on myös polynomifunktioiden kuvaajia koskevasta intuitiosta. Seuraavassa malliksi pari kuvaajaa:

[Kuvaaja]

\begin{displaymath}P(x)=\frac{1}{1440}x^8-\frac{1}{40}x^7+\frac{53}{144}x^6-\fra... ...1440}x^4-\frac{1189}{40}x^3+\frac{2537}{72}x^2-\frac{77}{ 5}x+1\end{displaymath}

[Kuvaaja]

\begin{displaymath}Q(x)=\frac{13}{20160}x^8-\frac{13}{560}x^7+\frac{491}{1440}x^... ...}x^4-\frac{2111}{80}x^3+\frac{16451}{560}x^2-\frac{279}{ 28}x-1\end{displaymath}

Nojaudumme Descartesin merkkisäännön perustelussamme polynomin ja sen derivaatan nollakohtien vuorovaikutukseen, joka näkyy edellisissä kuvissakin. Oletamme seuraavassa, että $f$ on polynomifunktio. $f$:n derivaatta $f'$ on myös polynomifunktio. Jos $a$ ja $b$, $a<b$, ovat $f$:n kaksi peräkkäistä positiivista 0-kohtaa, siis $f(a)=f(b)=0$, mutta $f(x)\ne 0$, kun $a<x<b$, niin $f$ saa välillä $[a,\,b]$ joko positiivisen maksimiarvon jossain pisteessä $c$ tai negatiivisen minimiarvon jossain pisteessä $c$. Kummassakin tapauksessa $f'(c)=0$. Polynomin kahden nollakohdan välissä on siis ainakin yksi derivaatan nollakohta. Jos $f$:n kaikki positiiviset nollakohdat ovat $x_1$, $x_2$, ..., $x_m$, niin $f'$:lla on ainakin $m-1$ nollakohtaa väleillä $(x_1,\,x_2)$, $(x_2,\,x_3)$, ..., $(x_{m-1},\,x_m)$.

Entä väli $[0,\,x_1]$? Jos $f(0)> 0$ ja $f'(0)<0$, ei $f'$:lla tarvitse olla yhtään nollakohtaa välillä $[0,\,x_1]$. Tästä on esimerkki polynomi $P$ yllä. Mutta jos $f(0)\ge 0$ ja $f'(0)>0$, $f$ saa pienillä positiivisilla arvoilla suurempia arvoja kuin $f(0)$. Tällöin $f$ saa välttämättä myös positiivisen maksimiarvon välillä $(0,\,x_1)$. Silloin $f'$:lla on nollakohta myös välillä $(0,\,x_1)$. Vastaavasti, jos $f(0)<0$ ja $f'(x)>0$, ei $f'$:lla tarvitse olla nollakohtaa välillä $(0,\,x_1)$, mutta jos $f(0)\le 0$ ja $f'(0)<0$, tällainen nollakohta on olemassa. Esimerkkinä polynomi $Q$ yllä. Jos $f'(0)=0$, derivoidaan lisää, kunnes tullaan nollasta eroavaan derivaatan arvoon $f^{(k)}(0)$. Samat johtopäätökset, jotka edellä tehtiin $f(0)$:n ja $f'(0)$:n merkeistä voidaan nyt johtaa $f(0)$:n ja $f^{(k)}(0)$:n merkeistä.

Jos edellinen päättely luetaan toisin, se merkitsee, että polynomin derivaatan positiivisten nollakohtien lukumäärä antaa ylärajan itse polynomin positiivisten nollakohtien lukumäärälle. Ja tämä yläraja riippuu siitä, ovatko $f(0)$ ja $f'(0)$ (tai $f(0)$ ja pienintä kertalukua $k$ oleva $f^{(k)}(0)$) erimerkkisiä vai ei. Jos $f(0)$ ja $f'(0)$ eivät ole erimerkkisiä, jokaisen kahden nollakohdan ja 0:n ja pienimmän positiivisen nollakohdan välissä on ainakin yksi derivaatan nollakohta. Funktion positiivisten nollakohtien määrä ei siis voi ainakaan ylittää derivaatan positiivisten nollakohtien määrää. Mutta jos $f(0)$ ja $f'(0)$ ovat erimerkkiset, tiedetään vain, että jokaisen kahden funktion positiivisen nollakohdan välissä on derivaatan nollakohta, mutta tällaista ei välttämättä ole 0:n ja funktion pienimmän positiivisen nollakohdan välissä. Tässä tapauksessa funktiolla voi olla yksi positiivinen nollakohta enemmän kuin derivaatalla.

Mutta miten tämä liittyy Descartesin merkkisääntöön eli polynomin $P$ kertoimien merkeistä koostuvaan jonoon? Lasketaan $P$:n ja sen derivaattojen arvot nollassa: ilmeisesti $P(0)=a_0$, $P'(0)=a_1$, $P''(0)=2a_2$ ja yleisesti

\begin{displaymath}P^{(k)}(0)=k(k-1)(k-2)\cdots 2\cdot 1\cdot a_k=k!a_k.\end{displaymath}

Erityisesti $P^{(n)}(x)=P^{(n)}(0)=n!$ kaikilla $x$. $P$:n kertoimien merkit ovat siis samat kuin $P$:n nollassa laskettujen eri kertaluvun derivaattojen merkit. Mutta nyt voidaan soveltaa edellistä päättelyä. Olkoot $m_1$, $m_2$, ..., $m_k$ ne indeksit $m$, joilla $a_m\ne0$. Nyt siis $n-1\ge m_1>m_2>\dots>m_k\ge 0$. Funktiolla $P^{(n)}(x)$ ei ole yhtään nollakohtaa. Ensinnäkin $P^{(n)}(0)>0$. Jos $a_{m_1}>0$ eli $P^{(m_1)}(0)> 0$, niin funktiolla $P^{(m_1)}$ ei ole yhtään positiivista nollakohtaa, mutta jos $a_{m_1}<0$ eli $P^{(m_1)}(0)<0$, niin funktiolla $P^{(m_1)}$ voi olla yksi positiivinen nollakohta. Samoin, jos $a_{m_1}$ ja $a_{m_2}$ ovat samanmerkkiset, $P^{(m_2)}$:n positiivisten nollakohtien määrä on enintään sama kuin $P^{(m_1)}$:n positiivisten nollakohtien määrä, kun taas $a_{m_1}$:n ja $a_{m_2}$:n erimerkkisyys sallii $P^{(m_2)}$:lle mahdollisesti yhden nollakohdan enemmän kuin mitä $P^{(m_1)}$:llä on. Mutta nämä havainnot on helppo muuttaa induktiotodistukseksi sille, että merkinvaihtojen määrä jonossa $(1,\,a_{m_1},\,a_{m_2},\,\dots,\,a_{m_k})$ antaa enimmäismäärän polynomin $P$ positiivisten nollakohtien määrälle. Descartesin merkkisäännön positiivisia nollakohtia koskevalle osalle on saatu perustelu.

Negatiivisten juurien lukumäärää koskevasta osuudesta selviämme helpommin. Polynomin $P(x)$ negatiiviset juuret ovat polynomin $Q(x)=P(-x)$ positiivisia juuria. Siitä, miten etumerkki käyttäytyy parillisessa ja parittomassa potenssissa seuraa, että jos kaikki kertoimet $a_k$ ovat $\ne 0$, niin jokaisesta kahdesta peräkkäisestä $P$:n samanmerkkisestä kertoimesta tulee kaksi peräkkäistä erimerkkistä $Q$:n kerrointa ja jokaisesta peräkkäisestä erimerkkisestä $P$:n kertoimesta tulee kaksi peräkkäistä samanmerkkistä $Q$:n kerrointa. Näin ollen $Q$:n kertoimien jonossa on merkinvaihto aina silloin, kun $P$:n kertoimien jonossa ei ole. Mutta tämä merkitsee, että $Q$:n positiivisten nollakohtien lukumäärä on enintään yhtä suuri kuin $P$:n kertoimien merkkijonossa olevien peräkkäisten samojen merkkien parien lukumäärä. Tämä perustelee Descartesin merkkisäännön negatiivisia juuria koskevan osan.

Muistutetaan vielä, että merkkisääntö antaa juurten lukumäärälle vain ylärajan. Juuria voi olla vähemmän. Merkkisääntö sallisi esimerkiksi polynomille

\begin{displaymath}P(x)=x^5-x^4+x^3-x^2+x-1\end{displaymath}

viisi positiivista juurta, mutta koska $P(x)=(x-1)(x^4+x^2+1)$, tällaisia juuria ei ole kuin yksi.
Solmu 3/2001
2001-11-05