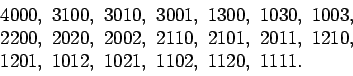
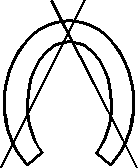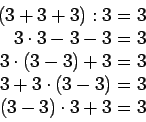Ratkaisut 3


1. Summasta saa siten parillisen, että kaksi parillista tai kaksi paritonta lukua lasketaan yhteen. Ensimmäisen kertolaskun tulos sisältää tekijän 18 ja on siis parillinen, joten toisen kertolaskun tuloksen on myös oltava parillinen. B-lasissa on siis 32 ja A-lasissa 19 kuulaa.


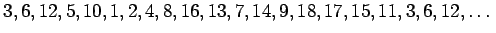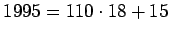2. $3, 6, 12, 5, 10, 1, 2, 4, 8, 16, 13, 7, 14, 9, 18, 17, 15, 11, 3, 6, 12,\ldots$ Lukujonon 19. jäsen on sama kuin ensimmäinen eli lukujonossa toistuu 18 jäsenen jakso. Lukujonon 1995. jäsen on 18-jäsenisen jakson 15. luku eli luku 18 ( $1995=110\cdot 18+15$).


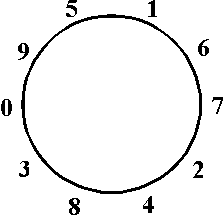
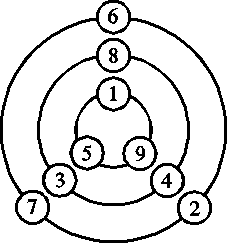
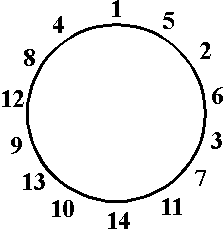
3. Kahden lapsen välissä, molemmissa puoliympyröissä seisoo yhtä monta lasta. Luvun 10 saaneen ja luvun 43 saaneen lapsen välissä on 32 lasta. Niin ikään toisessakin puoliympyrässä on 32 lasta. Yhteensä (kahden valitun lapsen kanssa) 32+32+2=66 lasta seisoo piirissä.


4. Ei ole mahdollista, että luvut olisivat lopuksi samoja. Koska alussa taululla olevien lukujen summa on pariton ( 1+9+9+6=25) ja luvuista aina kaksi vaihdetaan yhtä suurempiin, niin summa pysyy parittomana. Neljän saman luvun summa ei voi olla pariton.


5. Isäni on 23 vuotta vanhempi kuin minä. 46-vuotiaana hän on kaksi kertaa niin vanha kuin minä eli olen nyt 23-vuotias.


6. Rusina-porsaan ja Juuso-koiran väitteet eivät voi molemmat olla tosia, joten toinen valehtelee. Täten Mörri-kissan väite oli totta, että Juuso valehteli. Juuso söi vaniljakastikkeen.


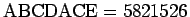7. Yhteenlaskun viimeisessä sarakkeessa olevan E:n arvo voi olla vain 6. Viimeistä edellisen sarakkeen C:n arvo voi olla joko 7 tai 2. C:n saadessa arvon 2 voi tehtävän ratkaista... $\text{ABCDACE}=5821526$.


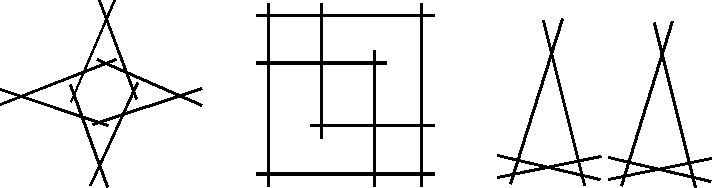
8. Muutamia ratkaisuja ohessa.





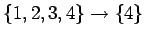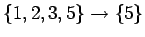9. Järjestys (D) ei ole mahdollinen, koska silloin sihteeri olisi saanut ensimmäiset neljä kirjettä ja kirjoittanut näistä ensin neljännen kirjeen (merkitään sitä näin: $\{1,2,3,4\}\rightarrow\{4\}$). Sen jälkeen hän olisi saanut viidennen kirjeen ja kirjoittaisi sen ( $\{1,2,3,5\} \rightarrow\{5\}$). Pöydällä olevien kirjeiden järjestys olisi silloin $\{1,2,3\}$. Jos siis kahden ensimmäisen kirjeen kirjoitusjärjestys olisi 4 ja 5, niin silloin järjestys voisi olla vain 4-5-3-2-1. Neljän muun järjestyksen toteutuminen:

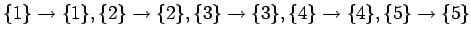(A) $\{1\}\rightarrow\{1\},\{2\}\rightarrow\{2\},\{3\}\rightarrow\{3\}, \{4\}\rightarrow\{4\},\{5\}\rightarrow\{5\}$;
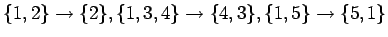(B) $\{1,2\}\rightarrow\{2\},\{1,3,4\}\rightarrow\{4,3\}, \{1,5\}\rightarrow\{5,1\}$;
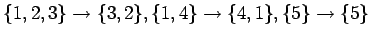(C) $\{1,2,3\}\rightarrow\{3,2\},\{1,4\}\rightarrow\{4,1\}, \{5\}\rightarrow\{5\}$;
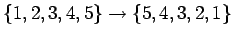(D) $\{1,2,3,4,5\}\rightarrow\{5,4,3,2,1\}$.



10. Muutamia ratkaisuja ohessa.





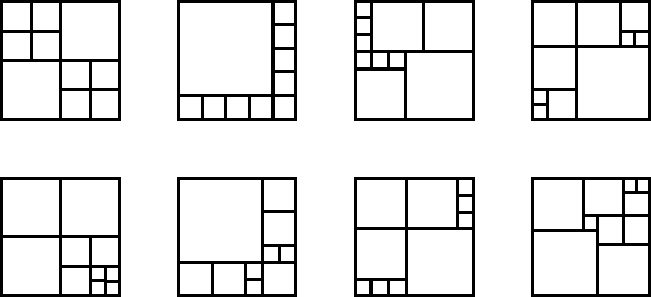
11. Yhden ja sadan välissä on kymmenen sellaista lukua, joissa ykkösten paikalla on seitsemän, ja kymmenen sellaista, joissa seitsemän on kymmenten paikalla. Luku 77 sisältyy jo molempiin, joten summa 10+10-1=19 on lukujen määrä. Jokaisessa sataluvussa on aina 19 kappaletta numeron seitsemän sisältävää lukua. Lukujen 700 ja 799 sekä 1700 ja 1799 välissä on molemmissa sata etsittyä numeroa. Lukujen 1 ja 2000 välillä on 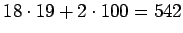$18\cdot19+2\cdot100=542$ kappaletta numeron 7 sisältävää lukua. Koska numeroa 7 etsitään lukuun 1995 asti, niin lukua 1997 ei lasketa mukaan eli etsittyjä lukuja löytyy 542-1=541 kappaletta.


12. Kokeillaan mahdollisuuksia, että tammikuun ensimmäinen päivä on maanantai, tiistai, jne. Jos tammikuun ensimmäinen päivä olisi maanantai, niin silloin myös 8., 15., 22., ja 29. olisivat maanantaipäiviä eli maanantaipäiviä olisi tammikuussa yhteensä viisi. Tehtävän väite on totta, kun tammikuun ensimmäinen päivä on tiistai.


13. Yksi ulpukka peittää lammesta puolet 111 päivän kuluessa, 110 päivän kuluessa neljäsosan ja 109 päivän kuluessa kahdeksasosan. Täten kahdeksan ulpukkaa kasvaa lammen umpeen 109 päivässä.


14. Lukujonoon saadaan seuraava jäsen siten, että viimeisimpään lukuun lisätään luvun numeroiden summa. Seuraava luku on siis 127+(1+2+7)=137.


15. Jos joko Vieno tai Kaino oli vaatimattomin, niin sekä Eino että Aino puhuivat totta, eikä se ole mahdollista. Jos taas Eino oli vaatimattomin, Vieno ja Kaino olisivat olleet oikeassa, mutta sekään ei ole mahdollista. Aino oli vaatimattomin ja Eino puhui totta.


16.




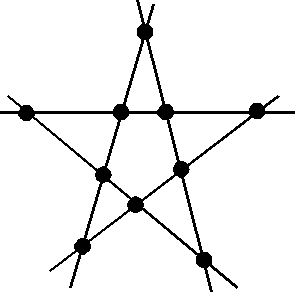
17.
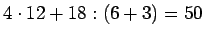a) $4\cdot12+18:(6+3)=50$;
b) 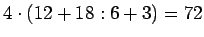$4\cdot(12+18:6+3)=72$;
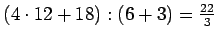c) $(4\cdot12+18):(6+3)=\frac{22}{3}$.



18. Luku 7 voi esiintyä missä tahansa kolmesta joukosta.


19. Summan ensimmäinen ja toinen luku voivat olla jotkin seuraavista: 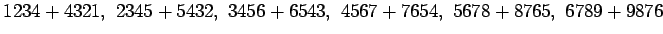$1234+4321,\ 2345+5432,\ 3456+6543,\ 4567+7654,\ 5678+8765,\ 6789+9876$. Näiden summien arvoja lukuun 17967 vertaamalla saadaan ainoaksi mahdolliseksi ratkaisuksi 4567+5764+7654=17967.


20. Jos ajateltu luku olisi 1 ja 100 väliltä, silloin Anna ja Pasi olisivat puhuneet totta, eikä se pidä paikkaansa. Jos taas luku olisi 201 ja 300 väliltä, olisivat Pasi ja Kirsti olleet oikeassa, mutta sekään ei ole mahdollista. Siksi etsitty luku on 101 ja 200 väliltä, ja niiden väliltä kannattaa etsimistäkin jatkaa.


21.



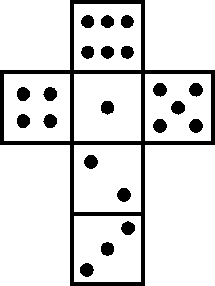
22. Hahmotellaan nopan rakenne. Siitä on nähtävissä, että eri asennoissa alimmalla sivulla on 2,4 ja 1 pistettä.





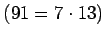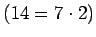23. 91 kynttilän pätkistä voidaan valmistaa $(91=7\cdot 13)$ 13 kynttilää. Näiden 13 kynttilän ja 92. kynttilän pätkistä $(14=7\cdot 2)$ saadaan kaksi uutta kynttilää, joiden pätkistä ei pysty valmistamaan enää uusia. Siten säästäväinen setä pystyy polttamaan 92+13+2=107 kynttilää.


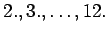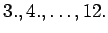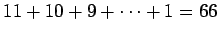24. 1. pysäkillä kyytiin noussut saattoi jäädä kyydistä $2.,3.,\dots,12.$ pysäkillä, tästä saadaan 11 erilaista matkaa. 2. pysäkillä kyytiin tullut taas saattoi jäädä pois $3.,4.,\dots,12.$ pysäkillä ja tästä tulee 10 erilaista matkaa. 11. pysäkillä kyytiin tullut saattoi jäädä 12. pysäkillä pois. Täten tällä matkalla pystyi matkustamaan korkeintaan $11+10+9+ \dots +1=66$ erilaista matkaa.


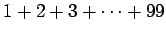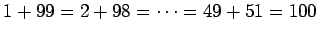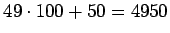25. Ensimmäisiin 99 joukkoon kirjoitetaan $1+2+3+\dots +99$ kappaletta lukuja. $1+99=2+98=\dots =49+51=100$. Luvulle 50 ei ole paria, kaikkiaan pareja on 49. Summaksi saadaan $49\cdot100+50=4950$. Niin 100. joukon ensimmäinen luku on 4951.


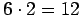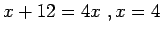26. Nuorin prinsseistä sai isältään x kpl linnoja. Hän sai isoveljiltään $6 \cdot 2 =12$ linnaa, joten hänellä oli siten x+12 linnaa. Keskimmäinen prinssi sai isältään 4x linnaa ja antoi pikkuveljilleen yhtä monta linnaa kuin sai isoveljiltään. Näillä molemmilla prinsseillä oli loppujen lopuksi yhtä monta linnaa eli $x+12=4x \ , x=4$. Prinssit saivat 4,8,12,16,20,24 ja 28 linnaa. Kuninkaalla oli siis 112 linnaa.


27. Tytöt ehtivät tunnelin läpi 12 minuutissa. Ensin Liisa ja Maija menevät tunnelin läpi (2 min), Liisa tulee takaisin (1 min) ja antaa lampun Kaisalle ja Hannalle, ja he menevät tunnelin läpi (5 min), Maija tulee takaisin (2 min) ja menee vielä kerran tunnelin läpi Liisan kanssa (2 min).


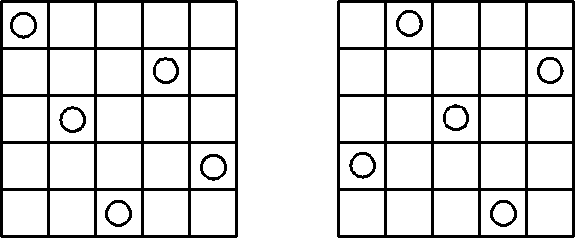
28. Kyllä voi. Katso kuvaa.





29. Kyllä voi. Katso kuvaa.





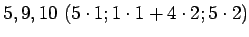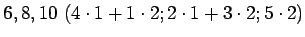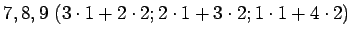30. Lapset ovat joko $5,9,10 \ (5\cdot 1 ; 1\cdot 1 +4 \cdot 2 ; 5\cdot 2)$ tai $6,8,10 \ (4\cdot 1+1\cdot 2;2\cdot 1+3\cdot 2;5\cdot 2)$ tai $7,8,9 \ (3\cdot 1+2\cdot 2;2\cdot 1+3\cdot 2;1\cdot 1+4\cdot 2)$ -vuotiaita.


31. Kolme kilpailijaa saavat yhteensä korkeintaan 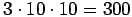$3\cdot10\cdot10=300$ pistettä. Jos kilpailija nro 2 vastasi kerran väärin, silloin kilpailija nro 1 on vastannut 4 kertaa väärin. He siis menettivät yhteensä vähintään (1+4)(10+5)=75 pistettä.(He eivät siis saaneet oikean vastauksen 10 pistettä ja lisäksi menettivät vielä 5 väärästä vastauksesta.) Näin siis 3 kilpailijaa saivat korkeintaan 300-75=225 pistettä. Kilpailijat saivat kuitenkin yhteensä 240 pistettä. Kilpailija nro 2 vastasi siis kaikkiin kysymyksiin oikein ja näin kilpailijalla nro 1 oli 3 vähemmän eli 7 oikeaa vastausta. 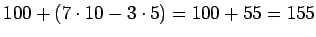He saivat siis yhteensä $100+(7\cdot 10-3\cdot 5)=100+55=155$ pistettä. Kilpailijan nro 3 pistemäärä on siis 240-155=85, se on 15 pistettä vähemmän kuin maksimipisteet, mikä tarkoittaa sitä, että hän teki yhden virheen. Yhteenveto: kilpailijoilla oli 7, 10 ja 9 oikeaa vastausta.


32. Kahta laikkua lukuunottamatta kaikki laikut ovat valkoisia, siksi kahdesta toinen on musta ja toinen ruskea. Kahta laikkua lukuunottamatta laikut ovat mustia, siksi kahdesta laikusta toinen on valkoinen ja toinen ruskea. Juhlapuvussa on siis 3 laikkua, 1 valkoinen, 1 musta ja 1 ruskea. (Sitä tietoa, että kahta lukuunottamatta kaikki laikut ovat ruskeita, ei enää tarvita.)


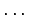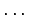33. Kyse on siitä, että kun isoäidin ikään lisätään sen numeroiden summa, saadaan 72. Numeroiden summa voi olla korkeintaan 6+9=15. Tämän takia täytyy tutkia lukua 72-15=57 suuremmat luvut lukuun 72 asti. 58+(5+8)=71, 59+(5+9)=73, $\ldots$, 63+(6+3)=72, $\ldots$ Ainoa ratkaisu on: isoäiti on 63-vuotias.


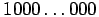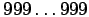34. Tarkasteltavat kaksi lukua ovat $1000\ldots 000$ ja $999\ldots999$. Niiden summa loppuu numeroon 9 ja erotus numeroon 1, joten tutkitun tulon viimeinen numero on 9.


35.

 H IDA S
 H IDA S
+HI DAS
--- ---
 LIHAS
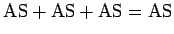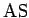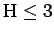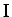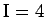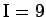Kahdessa oikeanpuoleisessa sarakkeessa $\text{AS}+\text{AS}+\text{AS}=\text{AS}$ voi toteutua, tulipa sarakkeista muistinumeroa tai ei, vain kun $\text{AS}$ tarkoittaa lukua 50. Vasemmassa reunassa on havaittavissa, että $\text{H}\leq 3$. $\text{I}$ (toinen sarake vasemmalta) ei voi olla 5 eikä 0, sillä nämä numerot ovat jo varattuja. Muistinumero huomioon otettuna $\text{I}=4$ tai $\text{I}=9$. 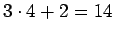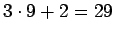$3\cdot4+2=14$, $3\cdot9+2=29$. 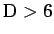Kummassakin tapauksessa keskimmäisestä sarakkeesta viedään muistinumerona 2, siksi $\text{D}>6$. Muutamien kokeilujen jälkeen saadaan tulos 29750+29750+29750=89250. 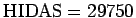$\text{HIDAS}=29750$.


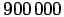36. $900\,000$.


37. Kysyttyjen lukujen keskimmäinen numero on 1 tai kolmas numero on 0. Näin kolmenumeroisia lukuja on 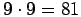$9\cdot9=81$ sekä 90 kappaletta. Yhteensä siis näitä lukuja on 81+90=171.


38. Aluksi keltaisesta väriliidusta sotkeentuu 1 cm verran. Kun liitua vedetään alaspäin, se sotkeentuu 2 cm matkalta. Takaisin liikutettaessa myös sininen väriliitu sotkeentuu 2 cm matkalta (sisältää alkuperäisen 1 cm). Näin joka kerta alaspäin liikutettaessa keltainen väriliitu sotkeentuu 1 cm enemmän ja takaisin työnnettäessä siniseen väriliituun sotkettu alue kasvaa 1 cm verran. 20 liikkeen lopussa molemmat väriliidut ovat siis sotkeentuneet 11 cm verran (sisältäen alkuperäisen 1 cm).


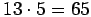39. Tasapelissä pelaajat saavat yhteensä 4 pistettä, voitosta taas 5 pistettä (eli 1 enemmän kuin tasapelistä). Barbapapa ja Barbamama pelasivat 13 peliä. Jos peleistä yksikään ei olisi päättynyt tasapeliin, pisteitä olisi kertynyt yhteensä $13\cdot 5=65$. Se on siis 5 pistettä enemmän kuin he todellisuudessa saivat eli tasapelejä oli 5. Barbamama sai tasapeleistä $5\cdot 2=10$ pistettä, voitoista kolme kertaa niin paljon eli $3\cdot 10=30$ pistettä. Hän sai nämä 30 pistettä 6 voitosta. Barbamama hävisi siis 13-(5+6)=2 peliä, toisin sanoen Barbapapa voitti 2 peliä.


40. Kyllä voi.





41. 2899.


42. Oletetaan, että hevoskauppiaalla oli aluksi 1000 markkaa. Ensimmäiset kaupat tehtyään hänelle jäi vielä 400 markkaa ostamansa hevosen lisäksi. Kun kauppias sitten myi hevosen, hänellä oli kaikkiaan 1100 markkaa. Ostettuaan hevosen uudelleen jäi taskuun vielä 300 markkaa ja kun hän toisen kerran myi hevosen, tällä kertaa 900 markalla, oli hänellä yhteensä 1200 markkaa. Kauppias siis voitti hevoskaupoillaan 200 markkaa.


43. Merkitään kääpiöiden lukumäärää a:lla ja muodostetaan seuraava yhtälö: 8a - 3 = 7a + 4, josta saadaan a = 7. Kääpiöitä oli siis seitsemän, ja mehutynnyri maksoi 53 penniä.


44. Alla olevassa kuvassa on esitetty kaksi mahdollista ratkaisua. Niitä peilaamalla ja kääntämällä saadaan vielä uusia ratkaisumahdollisuuksia.





45. Ruudukkoon sijoitettavien lukujen summa on 333. Jos siis lasketaan kullakin kolmella rivillä olevat kolme lukua yhteen, voidaan päätellä, että jokaisella vaaka- ja pystyrivillä sekä molemmilla lävistäjillä olevien lukujen summan on oltava yksi kolmasosa 333:sta, siis 111. Tarkastellaan ruudukon lävistäjillä ja keskimmäisellä vaakarivillä olevien lukujen muodostamia kolmea summaa. 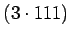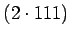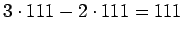Näiden summasta $(3 \cdot 111)$ vähennetään kahdella ulommaisella pystyrivillä olevien lukujen summa $(2 \cdot 111)$ ja erotukseksi saadaan $3 \cdot 111 - 2 \cdot 111 = 111$, joka on kolme kertaa niin suuri kuin ruudukossa keskimmäisenä oleva luku. 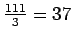Niinpä ruudukon keskimmäisessä ruudussa on $\frac{111}{3} = 37$. Edelleen havaitaan, ettei lukua 73 voi sijoittaa nurkkaruutuun. Edellä saadusta päädytään lyhyen päättelyn jälkeen alla olevassa kuvassa esitettyyn ratkaisuun (josta muut ratkaisut eivät oleellisesti poikkea).





46. On helposti havaittavissa, ettei yhdellä osumalla vielä pysty pudottamaan sellaisia purkkeja, joihin merkittyjen lukujen summa olisi 50. Kahdella heitolla tämä sen sijaan on jo mahdollista: jos osutaan purkkeihin, joiden kyljessä on luvut 4 ja 10, putoavat 4-purkin lisäksi 5-, 1- ja 11-purkit sekä 10-purkin mukana taas 8-, 2- ja 9-purkit. Näiden lukujen summa on 50.





47. Timon mukaan sininen ja keltainen ovat valkoisen naapureina, siksi sininen väri ei voi olla valkoista vastapäätä. Samasta syystä Pertin väittämän mukaan myös vihreä ja oranssi ovat poissa laskuista, ja niin valkoisen kanssa voi olla vastatusten vain punainen. Jotta oltaisiin varmoja tuloksen paikkansapitävyydestä, koetetaan vielä piirtää tehtävässä annetut ehdot täyttävä noppa, jossa valkoinen on punaista vastapäätä. Alla kuva tällaisesta nopasta tasoon levitettynä.





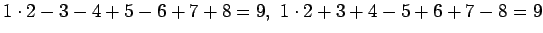48. $1 \cdot 2 - 3 - 4 + 5 - 6 + 7 + 8 = 9,\ 1 \cdot 2 + 3 + 4 - 5 + 6 + 7 - 8 = 9$.


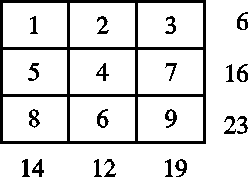
49. Ensimmäisellä rivillä olevien kolmen luvun summa voi olla 6 vain, jos kyseiset kolme lukua ovat 1,2 ja 3. Jotta kolmannen rivin lukujen summaksi tulisi 23, täytyy lukujen olla 6, 8 ja 9. Täten toisella rivillä olevat luvut ovat 4, 5 ja 7. Pystyriveistä kolmannella olevien lukujen summaksi saadaan 19 vain, jos luvut ovat 3, 7 ja 9. (Kiinnitä huomiota siihen, mihin järjestykseen kirjoitat luvut vaakariveille!) Tämän jälkeen vielä sijoittamatta olevien lukujen järjestys ratkeaakin helposti. Annetun ratkaisun ohella tehtävään on olemassa toinenkin ratkaisumahdollisuus. Siinä luvut 1 ja 2 sekä 4 ja 5 vaihtavat keskenään paikkoja.





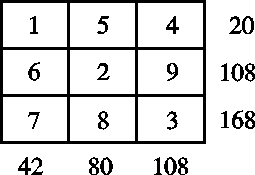
50. Luvut 42 ja 168 ovat molemmat 7:llä jaollisia, siksi alimman vaakarivin ensimmäiseen ruutuun tulee luku 7. Koska 20 ja 80 ovat 5:llä jaollisia, niin ylimmän rivin toiseen ruutuun kirjoitetaan luku 5. Tehtävässä annetuista tuloista ainoastaan 108 on 9:llä jaollinen, siten luku 9 tulee keskimmäisen rivin viimeiseen ruutuun. Yhtä yksiselitteisesti käy myös luvun 8 sijoittaminen oikealle paikalleen, minkä jälkeen loput luvut ovatkin helposti järjestettävissä taulukkoon sopiviin ruutuihin.





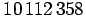51. $10\,112\,358$.


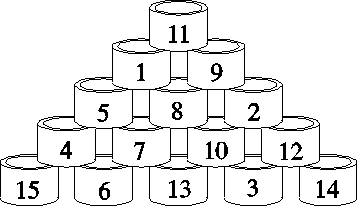
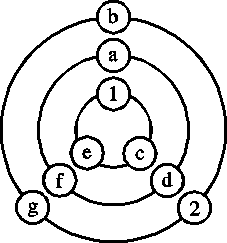
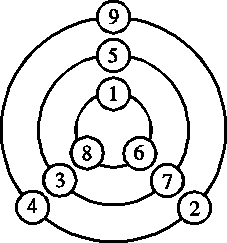
52. Jokaisella kolmella kehällä olevien lukujen summa on sama, ja näiden kolmen summan summa puolestaan on 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. Niinpä jokaisella kehällä (ja jokaisella suoralla) olevien lukujen summa on 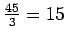$\frac{45}{3} = 15$. Suoralla tai kehällä, jonka luvuista yksi on 1, on kahden muun luvun summa oltava 14. 14 = 8 + 6, 14 = 9 + 5, muita mahdollisuuksia ei ole. Siten luvun 1 kanssa samalla suoralla olevia lukuja voivat olla 9 ja 5 tai 8 ja 6. Jos a = 9, niin silloin b = 5 ja g = 8, mikä ei voi pitää paikkaansa, sillä lukujen 1 ja 8 täytyisi olla samalla kehällä. Niinpä jos a = 5, on b = 9 ja g = 4. Tällä tavoin edelleen päättelemällä päästään kuvassa näkyvään ratkaisuun. Jos a = 6, ratkaisua ei ole. Jos taas a = 8, saadaan tehtävän toinen mahdollinen ratkaisu.





53. 196 - 163 = 33 ja 16 + 17 = 33. Siten arvausten 193 cm ja 163 cm virheet olivat 16 cm ja 17 cm, jos Antti olisi ollut 180 cm tai 179 cm pitkä. 185 - 178 = 7 ja 7 = 6 + 1, niinpä näiden arvausten ja virheiden tapauksessa Antti olisi taas ollut 184 cm tai 179 cm pitkä. Muita mahdollisuuksia Antin pituudeksi ei ole, ja siksi etsitty vastaus on 179 cm.


54.
 4 95
+4 59
-- --
 9 54



55. Tässä kolme ratkaisua:





56. Muutama ratkaisutapa

\begin{displaymath}\begin{split} (3+3+3):3 &= 3\\ 3 \cdot 3-3-3 &= 3\\ 3 \c... ...3+3 \cdot (3-3) &= 3\\ (3-3) \cdot 3+3 &= 3\\ \end{split} \end{displaymath}




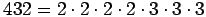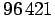57. $432=2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3$, minkä tähden luvussa voivat esiintyä numerot 2,4,8,3,9,6 ja 1. Jos numero 6 esiintyy, esiintyy myös numero 9 ja tällöin kakkosista tulee joko 8 tai yksi 2 ja yksi 4. (Jälkimmäisestä tapauksesta saadaan useampinumeroinen luku, joten valitaan se vaihtoehto.) Saatu luku on siis $96\,421$. Jos etsityssä luvussa ei esiinny numeroa 6, tulee kolmosista yksi 3 ja yksi 9, ja kakkosista tulee yksi 8 ja yksi 2. 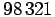Näin saatu luku on $98\,321$. 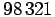Vastaus: Suurin luku on $98\,321$.


58. 3-numeroisten lukujen määrä on 900, näin 3-numeroisia parittomia lukuja on 450. 4-numeroisia lukuja on 9000 ja 4-numeroisia parittomia lukuja siis 4500. 4500+450=4950 kpl. Parillisen monen parittoman luvun summa on parillinen, joten kysytty summa on parillinen.


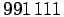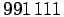59. Koska tehtävässä kysyttiin suurinta 6-numeroista lukua, valitaan ensimmäiseksi numeroksi 9. Voisiko myös toinen numero olla 9? Kyllä, esimerkiksi $991\,111$. Kolmas numero voi olla enää 1 (tai 0) ja loputkaan numerot eivät voi olla suurempia kuin 1, sillä muuten ensimmäinen 9 ei ole vähintään yhtä suuri kuin muiden numeroiden tulo. Saatiin siis luku $991\,111$. Jos asiaa pohditaan tarkemmin, löytyy vielä tätäkin suurempi luku. Kun mikä tahansa luku kerrotaan 0:lla, tulo on 0. 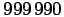Tehtävän vastaus: $999\,990$


60. Ruusan syntymäpäivää kysyttiin tammikuun ensimmäisenä päivänä. Ruusan syntymäpäivä on joulukuun 31. päivä. Toissapäivänä Ruusa oli vielä 10-vuotias, eilen - viime vuoden viimeisenä päivänä - Ruusa täytti 11 vuotta. Tänä vuonna hän täyttää 12 vuotta ja ensi vuoden viimeisenä päivänä 13 vuotta.


61. Koska värität neljä sivua kolmella eri värillä, jotain väriä on käytettävä kahden sivun värittämiseen. Jos tämä väri on esimerkiksi punainen, seuraavat väritystavat ovat mahdollisia:


Vastaavasti on aina 3 vaihtoehtoa, jos kaksi sivua väritetään vihreällä tai sinisellä. On siis 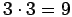$3\cdot 3=9$ tapaa värittää eri tavalla.


62.

      aa
$\cdot$    a a
-- -- --
      aa
+$\,$a aa  
-- -- --
   9a aa

Koska tulon ensimmäinen numero on 9, ensimmäinen osatulo on ainakin 890. Tämä toteutuu vain silloin, kuin kerrottavana on 99 ja kertojan ensimmäinen numero on 9. Toinen osatulo voi olla vain siinä tapauksessa 2-numeroinen luku, että 99 kerrotaan 1:llä.

Vastaukseksi saadaan näin ollen

      99
$\cdot$    91
-- -- --
      99
+$\,$89 1 
-- -- --
   900 9




63. Koska ensimmäinen ostaja osti mehua kaksi kertaa niin paljon kuin toinen, ostetun mehun määrä on kolminkertainen toisen ostajan mehun määrään verrattuna. Mehua oli kaiken kaikkiaan 31+20+19+18+16+15=119 litraa. Tästä saadaan 3:lla jaollinen luku vain silloin, kun 20 litran astia jää myymättä. Kaksi ostajaa osti siis yhteensä 99 litraa mehua. Toinen heistä osti 15+18=33 litraa ja toinen 16+19+31=66 litraa. 20 litran astia jäi myymättä.


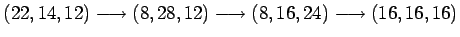
64. $(22,14,12) \longrightarrow (8,28,12) \longrightarrow (8,16,24) \longrightarrow (16,16,16)$


65. Helmistä voi saada 8 erilaista ketjua:

PSPSPSPS, PSSPSPSP, PSSPSSPP, PSSSPPPS,
PPSSPPSS, PPSPSSPS, PPSSSPPS, PPPPSSSS



66.

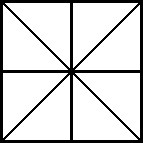
Koon mukaan laskien kuviossa on 4, 4 ja 8 samankokoista kolmiota. Oikea vastaus: kuviossa on 16 kolmiota.




68. Jos tiili painaa 2 kg ja puolen tiilen painon, puolikas tiili painaa 2 kg. Yksi tiili painaa 4 kg ja kaksi tiiltä 8 kg.


69. Jos parkkipaikalla olisi pelkkiä autoja, 15 kulkuvälineellä olisi 60 rengasta. Parkkipaikalla on kuitenkin 4 rengasta vähemmän, joten siellä voisi olla esimerkiksi 4 sivuvaunullista moottoripyörää ja 11 autoa, mutta tällöin parkkipaikalla ei olisi tavallisia moottoripyöriä. Renkaiden määrää voi alentaa 4:llä, jos yhden auton tilalle otetaan yksi moottoripyörä (renkaiden määrä vähenee kahdella) ja kahden auton tilalle kaksi sivuvaunullista moottoripyörää (renkaiden määrä vähenee 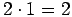$2\cdot 1=2$ kpl). Parkkipaikalla on 12 autoa, 2 sivuvaunullista moottoripyörää ja 1 tavallinen moottoripyörä.


70. Kirjaimen T saamiseksi sanan alusta sanan loppuun tarvitaan 4 siirtoa. Siirtojen jälkeen sana alkaa kirjaimella O. Sen siirtämiseksi neljännelle paikalle tarvitaan 3 siirtoa. Tämän jälkeen kirjaimen R siirtämiseksi paikallen tarvitaan 2 siirtoa. Kun vielä kirjaimet I ja A vaihtavat keskenään paikkoja, valmista tuli. Tarvitaan siis 4+3+2+1=10 siirtoa. (Jos kirjainten paikkoja vaihdetaan muussa järjestyksessä, siirtoja tarvitaan silloinkin vähintään 10.)


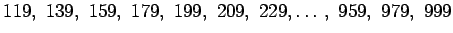71. Kysyttyjen lukujen viimeisen numeron on oltava 9, sillä muuten yhtä suuremman luvun numeroiden summa on yhtä suurempi kuin ko. luvun, ja silloin molempien lukujen numeroiden summa ei voi olla pariton. Edelleen vain sellaiset luvut kelpaavat, joiden kahden ensimmäisen numeron summa on parillinen: $119,\ 139,\ 159,\ 179,\ 199,\ 209,\ 229,\ldots, \ 959,\ 979,\ 999$. 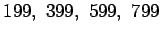Näistä luvuista täytyy kuitenkin jättää vielä pois luvut $199,\ 399,\ 599,\ 799$, sillä niitä seuraavien lukujen numeroiden summa on parillinen. Tehtävät ehdot täyttää siis 41 lukua.


72. Ruudukon keskirivillä 2. (ja 3.) ruudulla on vähintään yksi yhteinen kulma kaikkien paitsi yhden ruudun kanssa. (Keskirivin viimeinen/ensimmäinen ruutu.) Tämän takia keskirivin 2. ja 3. ruutuun voi sijoittaa ainoastaan luvut 1 ja 8. Kun nämä kaksi lukua on sijoitettu, taulukko on helppo täyttää loppuun. Ratkaisuja on useita.





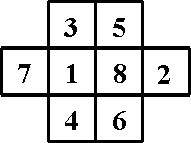
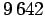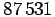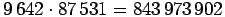73. $9\,642$ ja $87\,531$ ( $9\,642 \cdot 87\,531 = 843\,973\,902$).


74. Lukuja on 20:

\begin{displaymath}\begin{split} &4000,\ 3100,\ 3010,\ 3001,\ 1300,\ 1030,\ 100... ...0,\\ &1201,\ 1012,\ 1021,\ 1102,\ 1120,\ 1111. \end{split} \end{displaymath}




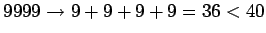75. Luku on silloin pienin, kun se muodostuu mahdollisimman pienestä määrästä numeroita eli numeroiden summa (40) täytyy muodostaa mahdollisimman vähäisestä määrästä luonnollisia lukuja. Koska $9999 \rightarrow 9+9+9+9 = 36 < 40$, kysytty luku on vähintään 5-numeroinen. 5-numeroisen luvun abcba keskimmäisen numeron on oltava parillinen, koska vain siinä tapauksessa a+b+c+b+a = 2a+2b+c on arvoltaan parillinen (=40). c = 0, 2, 4, 6 tai 8. 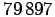Tapaukset läpi käymällä vastaukseksi löytyy luku $79\,897$.

Matematiikkalehti Solmu
2000-01-31