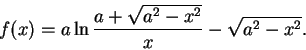PDF, PS

HTKK, TTKK, LTKK, OY, ÅA/Insinööriosastot
Valintakuulustelujen matematiikan koe 28.5.1997

1. Määritä parametrin a funktiona sen äärellisen tasoalueen pinta-ala, jonka paraabelit y=2ax²-ax-2a+2 ja y=ax²-2ax+4a+2rajaavat.

2. Määritä ne yksikkövektorit $\bar{u}=a\bar{i}+b\bar{j}+c\bar{k}$, jotka muodostavat yhtä suuren kulman vektoreiden $\bar{v}_{1}=\bar{i}$, $\bar{v}_{2}=5\bar{i}+12\bar{j}$ ja $\bar{v}_{3}=2\bar{i}+\bar{j}+2\bar{k}$kanssa.

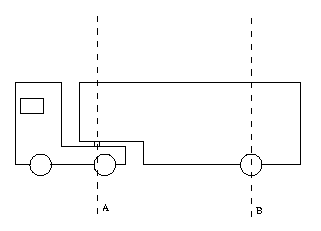
3. Jeppe Niilonpoika on löytänyt pullolleen hienon piilopaikan hyllyn suorakulmaisesta nurkasta kahden suuren sylinterinmuoteoisen maalipurkin takaa (kuva 1). Kuinka suuri voi täysin näkymättömissä olevan pullon halkaisija d enintaan olla, kun kummankin maalipurkin halkaisija on (tarkasti) 2 dm? Ilmoita pullon halkaisijan tarkka arvo (desimetreissä) ja likiarvo millimetreissä yhden yksikön tarkkuudella.

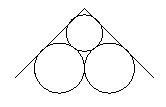
4. Binomin kuutiolle tunnetusti pätee kaava

(a+b)³=a³+3a²b+3ab²+b³=a³+b³+3ab(a+b).

Määritä tämän avulla yhtälön

$$\sqrt[3]{3+x}+\sqrt[3]{4-x}=\sqrt[3]{3}$$

reaaliset ratkaisut (tarkat arvot).

5. Täti Ruskea, Täti Vihreä ja Täti Sinipunainen huvittelivat joskus pienellä uhkapelillä. Pelin alussa he perustivat rahapotin, johon kukin tädeistä laittoi tietyn summan. Koko potin voittajasta he päättivät heittämällä kolmea noppaa (kussakin nopassa eri sivuilla silmäluvut 1, 2, 3, 4, 5 ja 6). Sovittiin seuraavasti: jos esiintyi kolme eri silmälukua (kaikki nopat osoittivat eri lukuja), Täti Ruskea voitti potin, jos esiintyi kaksi eri silmälukua (kaksi noppaa kolmesta osoitti samaa lukua), Täti Vihreä voitti potin, ja lopuksi, jos esiintyi vain yksi silmäluku (kaikki kolme noppaa osoittivat samaa lukua), Täti Sinipunainen voitti potin. Pelin alussa Täti Vihreä laittoi pottiin 15 äyriä. Kuinka paljon Täti Ruskean ja Täti Sinipunaisen tuli laittaa pottiin, jotta peli olisi ollut oikeudenmukainen? (Siihen aikaan, kun peliä pelattiin, 1 äyrin kolikko oli pienin raha.)

6. Rekan puoliperävaunu on kiinnitetty vetoautoon tapilla A (kuva 2), joka alkuhetkellä on xy-tason origossa. Perävaunun taka-akselin keskipiste B on alkuhetkellä x-akselin pisteessä (a,0), missä a>0. Kun vetovaunu lähtee liikkeelle, A liikkuu y-akselia pitkin ylöspäin, ja B liikkuu siten, että joka hetki sen liikesuunta on kohti A:n senhetkistä sijaintia. Osoita, että B kulkee pitkin käyrää y=f(x), missä

$$f(x)=a\ln\frac{a+\sqrt{a^{2}-x^{2}}}{x}-\sqrt{a^{2}-x^{2}}.$$