PDF, PS

HTKK, TTKK, LTKK, OY, ÅA/Insinööriosastot
Valintakuulustelujen matematiikan koe 28.5.1997
Ratkaisut


1. Sijoittamalla lämpötilan T lausekkeeseen t=0 ja T=100 saadaan C=80. Tällöin, sijoittamalla uudelleen t=20 ja T=60, saadaan $e^{-20k}=\frac{1}{2}$ ja $k=\frac{1}{20}ln2$, jokin \begin{equation*}T=20+80e^{-\frac{1}{20}\ln 2}=20+80 \cdot 2^{-\frac{1}{20}} \end{equation*}Jos tässä asetetaan lämpötilaksi T=30, tulee $2^{-t/20}=\frac{1}{8}$ ja t=60. Kysytty lisäaika on siten $60-20=\underline{40 \text{min}}.$

2. Olkoon x alennusten monikerta. Tällöin kilohinnaksi tulee $10 \, - \, 0,2x$, viikkomyynniksi $250 \, + \, 20x$ ja nettomyyntituloksi/viikko (10-0,2x-6)(250+20x). Nettomyyntifunktio saavuttaa maksiminsa, kun $x \, = \, 3,75$. Siten kysytty kilohinta on $10\,-\,0,2 \cdot 3,75 \,=\, 9,25$mk/kg 3.

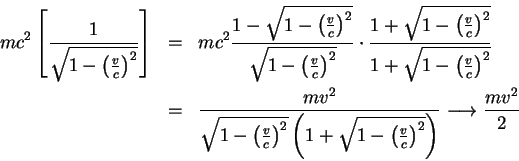
\begin{eqnarray*}mc^2 \left[ \frac{1} {\sqrt{1-\left(\frac{v}{c}\right)^2}} \ri... ...\frac{v}{c} \right)^2 } \right) } \longrightarrow \frac{mv^2}{2} \end{eqnarray*}


kun $c \rightarrow \infty$.

4. Merkitään $h=s \, \sin\alpha $ ja $x=s \, \cos\alpha $. Tällöin poikkileikkauksen ala on

\begin{equation*}f(\alpha)=(s+x)h=s^2(\sin\alpha \ + \ \cos\alpha \sin\alpha), \end{equation*}

missä $0 \le \alpha \le \pi / 2$. Ehdosta $f^{'}(\alpha)=0$ saadaan $\cos\alpha = \frac{1}{2}$ tai -1. Näistä -1ei kelpaa, koska $0 \le \alpha \le \pi / 2$ ja $\cos\alpha \ge 0$. Yhtälö $\cos\alpha = \frac{1}{2}$ antaa $\alpha=\pi/3$ $(=60^{\circ})$. Esimerkiksi f':n merkkivaihtelun perusteella $\alpha=\pi/3$ on paikallinen maksimikohta. Todetaan että se myös antaa funktion f suurimman arvon välillä $0 \le \alpha \le \pi / 2$. Siten vastaus on $\alpha=\pi/3$.

5. Helposti havaitaan että tasoon ei voi sisältyä mikään kuution särmistä. Siten taso on vinosssa asennossa kuution pohjaneliöön nähden ja sisältää sen lävistäjän. Se erottaa kuution soppeen tetdraedrinmuotisen kappaleen, jonka pohja on kolmio (puolet pohjaneliöstä) ja korkeusjana kuution särmä. Sen tilavuus on $\frac{1}{3} \cdot \frac{1}{2}a^2 \cdot a =\frac{1}{6}a^3$, missä a on kuution särmän pituus. Toisen leikkauksessa muodostuneen osan tilavuus on $a^3 -\frac{1}{6}a^3=\frac{5}{6}a^3$. Tämän ja edellisen osan tilavuuksien suhde on $\frac{5}{6}a^3 : \frac{1}{6}a^3=5$. 6. Ruuhka alkaa muodostua, kun raja 630 autoa/tunti eli 10,5 autoa/min ylittyy, ts. kun aika t (min), jolle \begin{equation*}8 + \frac{t}{10} =10,5 \ \textrm{eli} \ t=25, \end{equation*}on kulunut klo 16.00:sta. Tällöin kello on 16.25. Tämän jälkeen autoja kasaantuu aina klo 18.00 (120 min klo 16.00:sta) asti nopeudella $8+\frac{t}{10}-10,5$ eli $\frac{t}{10}-2,5$ autoa/min. Klo 18.00 autoja on kertynyt määrä

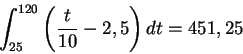
\begin{equation*}\int_{25}^{120}\left(\frac{t}{10}-2,5\right)dt=451,25 \end{equation*}

Viimeksi tullut (eli klo 18.00) joutuu odottamaan ajan $\frac{451,25}{10,5}=42,97 \approx \underline{43 \text{min}}$. Ruuhka On pahimmillaan juuri ennen kuin jono alkaa lyhentyä, ts. kun aika t (min), jolle \begin{equation*}24- \frac{t}{30}=10,5 \ \textrm{eli} \ t=405, \end{equation*}on kulunut klo 16.00:sta tällöin kello on 22.45. Klo 18.00 (t=120) jälkeen autoja on kertynyt lisää määrä

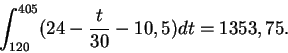
\begin{equation*}\int_{120}^{405}(24-\frac{t}{30}-10,5)dt=1353,75. \end{equation*}

Jonossa on pahimmillaan 451,25 + 1353,75 = 1805 autoa. Viimeksi tullut (eli klo 22.45) joutuu odottamaan ajan $\frac{1805}{10,5}=171,9 \approx \underline{172 \text{min}}$(=2h 52min).


Matematiikkalehti Solmu
2000-04-11