PDF

5. Matematiikkaa keskiajalla

Antiikin matematiikka alkoi sammua muun antiikin kulttuurin myötä ajanlaskumme ensimmäisinä vuosisatoina. Tuon ajan matemaattiset tekstit ovat enimmäkseen kommentaareja, uusia tuloksia syntyy enää vähän. Viimeinen merkittävä antiikin matemaatikko on aleksandrialainen Pappos (noin 320), jonka Matemaattinen kokoelma -teoksen sitaateissa on säilynyt useiden kymmenien antiikin geometrikkojen tekstejä. - Aleksandrialainen oli myös ensimmäinen nimeltä tunnettu naismatemaatikko Hypatia (370[?]-415; ''kauneudestaan, siveydestään ja opistaan kuuluisa naisfilosofi'' - Iso tietosanakirja, 1932). Hypatian tuotanto on kommenttiluonteista. Hän kärsi marttyyrikuoleman kristittyjen käsissä kieltäydyttyään luopumasta pakanallisista käsityksistään.

Rooman keisarikunta luhistui 400-luvulla. Roomalainen valtiomies, itägoottilaisten keisarien neuvonantaja ja filosofi Boëthius (480-524) kirjoitti muutamia jokseenkin alkeellisia oppikirjoja, jotka kuitenkin edustivat seuraavien vuosisatojen ajan korkeinta matematiikkaa länsimailla. Itä-Rooman alueella oli jonkin verran matemaattista toimintaa: Konstantinopolin Hagia Sofia -kirkon arkkitehdit Anthemius Trallesilainen (k. 534) ja Isidoros Miletolainen (n. 520) olivat myös matemaattisesti sivistyneitä ja mm. kiinnostuneita Arkhimedeen teoksista. Edellisen sanotaan esittäneen ellipsin konstruoinnin kahteen pisteeseen kiinnitetyn langan avulla. Jälkimmäinen oli viimeinen Platonin Akatemian johtaja. Itä-Rooman keisari Justinianus lakkautti akatemian v. 529. Tätä seuranneina vuosisatoina matematiikan tutkimus sammui länsimaissa kokonaan ja antiikin aikana löydetyt tulokset unohdettiin lähes kokonaan. Vaatimatonta matematiikan harrastusta esiintyi koululaitoksen piirissä: keskiajan koulun oppiaineisiin, ''seitsemään vapaaseen taiteeseen'' kuuluivat, pythagoralaisen esikuvan mukaan, mm. aritmetiikka ja geometria. Matematiikan opetus rajoittui kuitenkin aivan alkeisiin. Vasta renessanssin aikana alkaa länsimainen matematiikka uudelleen elpyä. Matematiikan kehityksen painopiste sijaitsee neljännestä kolmanteentoista vuosisataan ensin intialaisen ja sitten islamin kulttuurin piirissä.


5.1 Intia

Keskiajan intialainen matematiikka liittyy selkeästi babylonialaiseen aritmeettis-algebralliseen traditioon. Intialaisen matematiikan merkittävin anti lienee lukujen kymmenjärjestelmään perustuva merkitseminen ns. arabialaisilla numeroilla, siis nykyinen normaali merkintätapamme. Kaikki kymmenjärjestelmän ainekset löytyvät kyllä yksittäin aikaisemmista kulttuureista, mutta muualla (paitsi Kiinassa, jossa käytetyt ''sauvanumerot'' noudattivat oikeastaan 100-kantaista paikkajärjestelmää) niitä ei yhdistetty. Vanhimmat viittaukset hindulaiseen kymmenjärjestelmään löytyvät Aryabhatan (noin 500 jKr.) runomuotoisesta astronomis-matemaattisesta teoksesta Aryabhatija; varhaisin todella säilynyt esimerkki kymmenjärjestelmällä merkitystä luvusta - luku on 346 - on vuodelta 595. Nolla tuli kuitenkin käyttöön numeroiden merkinnässä vasta myöhemmin - itse asiassa vanhin Intiasta tunnettu 0-symbolin esiintymä on vasta 800-luvulta. Usein kuultu lause ''intialaiset keksivät nollan'' on hiukan epätarkka. Babylonialaista nollasymbolia ei kuitenkaan koskaan sijoitettu viimeiseksi numeroksi, joten nollan täysin nykykäsityksiä vastaava käyttö on todella peräisin hinduilta.

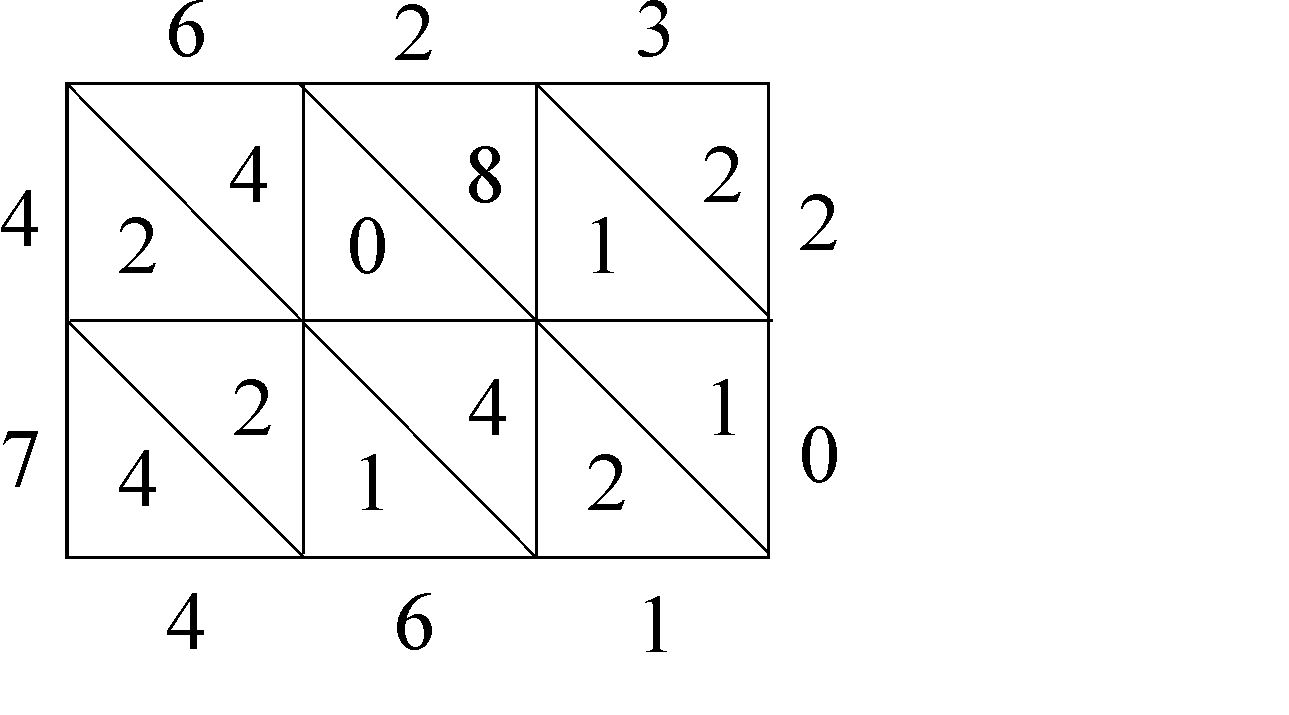
Tarkkaa selkoa kymmenjärjestelmään olennaisesti liittyvien laskualgoritmien alkuperästä ei ole. On esitetty perusteltuja olettamuksia, joiden mukaan sittemmin (1200-luvulta alkaen) ennen muuta Italiassa julkaistuissa laskuoppaissa esiintyvät metodit kuten gelosia-kertolasku ja kaleeri-jakolasku olisivat alkuaan intialaisia. Nykyiset algoritmit ovat olennaiselta sisällöltään samat, vaikka numeroiden sijoittelussa laskukaavioihin onkin tapahtunut (ja tapahtuu edelleen!) muutoksia.

Gelosia-kertolaskulla $74\cdot 623=46102$ järjestyy näin

ja galeoni-jakolaskulla

\begin{displaymath}\frac{78963}{245}=322+\frac{73}{245} \end{displaymath}

näin:
            /1            
          /1 /5 7          
          /5 /4 /6 3        
2 4 5 | /7 /8 /9 /6 /3 | 3 2 2
        /7 /3 /5 /0 /0        
          /4 /9 /9          
            /4            

Kymmenjärjestelmän ohella toinen pysyvään ja yleiseen käyttöön jäänyt intialainen innovaatio on trigonometrian sinifunktio: intialaisten tähtitieteilijöiden ajanlaskumme alkuvuosisatoina laatimiin Siddhanta-nimisiin runomuotoisiin esityksiin liittyi kaksinkertaisen kulman jänteen puolikkaan taulukoita. Intialaiset taulukot noudattivat kulmajakoa $3^\circ45'$; tarkemmat arvot interpoloitiin. Ptolemaioksen taulukko oli käyttänyt vastaaviin tarkoituksiin koko kulmaa vastaavia jänteitä. (Nimitys sini, latinan sinus, johtuu väärinkäsityksestä: sanskritin jänteen puolikasta tarkoittava jya-ardha vääntyi arabiaan muodossa jiba. 1100-luvun kääntäjä luki termin virheellisesti muodossa jaib. Tämä sana tarkoitti lahtea, rintaa tms. kaarevaa objektia kuten latinan sinus.)

Huomattavin varhaiskeskiajan matemaatikko oli Brahmagupta (noin 625). Intialaiselle matematiikalle tyypilliseen tapaan hänen tuotantonsa oli epätasaista: oikeat ja vähemmän oikeat tulokset esiintyvät rinta rinnan, esim. ympyrän kehän ja halkaisijan suhteen arvot $\sqrt{10}$ ja 3. Tunnettu Heronin kaavalle analoginen Brahmaguptan kaava nelikulmion pinta-alalle S,

\begin{displaymath}S=\sqrt{(s-a)(s-b)(s-c)(s-d)}, \end{displaymath}

(s on nelikulmion piirin puolikas) pätee itse asiassa vain ympyrän sisään piirrettyihin eli jännenelikulmioihin.

Merkittävin Brahmagupta oli aritmeetikkona: hän käytti ensimmäisenä nollaa ja negatiivisia lukuja johdonmukaisesti. Mm. sellainen sääntö kuin negatiivinen kertaa negatiivinen on positiivinen oli Brahmaguptalle tuttu. Toisen asteen yhtälöllä saattoi olla kaksi ratkaisua silloinkin, kun ratkaisut eivät olleet positiivisia. Brahmagupta ja hänen aikalaisensa Intiassa käyttivät sumeilematta myös irrationaalilukuja välittämättä niihin sisältyvistä loogisista vaikeuksista. Brahmagupta käytti kirjoituksissaan Diofantoksen tavoin eräänlaista algebrallista symbolismia. Brahmaguptan ansiolistaan kuuluu vielä ensimmäisen asteen Diofantoksen yhtälön ax + by = c täydellinen ratkaisu: Diofantos itse oli tyytynyt eri tehtävissa vain yksittäisratkaisuihin. Brahmagupta esitti myös metodin Pellin yhtälöiden x2-Dy2=1 ratkaisemiseksi. (Yhtälötyypin nimi johtuu 1600-luvulla eläneestä englantilaisesta John Pellistä, jonka on arveltu tutkineen tämänlaatuisia yhtälöitä; tieto on kuitenkin epävarma.) Jos x2-Dy2=a ja t2-Du2=b, niin x2+Dy'2=(xt+Dyu)2-D(xu+yt)2=(x2-Dy2)(t2-Du2)=ab. Jos x':lla ja y':lla on yhteinen tekijä, se voidaan supistaa, ja mahdollisesti päästä ratkaisuun.

Viimeinen huomattava keskiajan intialaismatemaatikko oli Bhaskara (1114-85), joka mm. kehitti edelleen Pellin yhtälöiden ratkaisutekniikkaa. Hän ratkaisi yhtälön x2=1+py2 tapauksissa p=8, 11, 32, 61 ja 67. Esimerkiksi yhtälön x2 = 1 + 61y2 ratkaisu $x = 1\,766\,319\,049$, $y = 226\,153\,980$. Bhaskara on kuuluisa myös yksisanaisesta (Katso!) Pythagoraan lauseen todistuksestaan, joka perustuu siihen, että c-sivuinen neliö voidaan jakaa neljäksi suorakulmaiseksi kolmioksi, joiden kateetit ovat aja b, sekä a-b-sivuiseksi neliöksi; c2=2ab + (a-b)2= a2+b2.


5.2 Islam

Islamin perustaja profeetta Muhammed kuoli vuonna 632. Noin sata seuraavaa vuotta islam oli sotaisessa ekspansiovaiheessa, mutta kahdeksannen vuosisadan puolivälistä alkaen islamilaisvaltioiden johtajat alkoivat suhtautua myönteisemmin myös kulttuuriin. Erityisesti kalifikunnan keskuksessa Bagdadissa ja sinne perustetussa Aleksandrian Museionia muistuttaneessa Dar al Hikmassa eli Viisauden talossa tutkittiin ja käännettiin arabiaksi kreikkalaisia käsikirjoituksia, ja myös kosketuksia Intiaan hyödynnettiin.

Matematiikan historialle islamin kulttuurin suurin merkitys on toisaalta antiikin perinnön tallettamisessa ja toisaalta intialaisen aritmetiikan omaksumisessa ja edelleen välittämisessä. Joissain tapauksissa arabialainen panos näkyy vain tuotteen nimessä: esim. Klaudios Ptolemaioksen tähtitieteellinen pääteos, jonka vaikutus keskiajan maailmankuvaan oli erittäin ratkaiseva, tunnetaan yleisesti arabiankielisellä nimellään Almagest. - On myös huomattava, että islamin kulttuuripiiri oli maantieteellisesti laaja ja sisälsi monia kansallisuuksia ja kieliä. Yhdistävä tekijä oli uskonto ja sivistyksen yhteinen kieli arabia.

Merkittävimmin arabimatemaatikoista on jälkimaailmaan vaikuttanut Muhammad ibn Musa Al-Khowarizmi (780[?]-850[?]). Al-Khowarizmi kirjoitti tähtitieteestä, mutta tärkeimmät hänen teoksistaan ovat aritmetiikan ja algebran oppikirjat. Edellinen on säilynyt vain latinankielisenä käännöksenä De numero indorum. Siinä selvitetään intialaisen kymmenjärjestelmän käyttö. Arabian kielessä ei ollut erityisiä numeromerkkejä, vaan numerot ilmaistiin kirjaimin. Teoksen osin huolimattomat latinalaiset käännökset ovat syypäitä nimitykseen arabialaiset numerot, vaikka Al-Khowarizmi itse ei mitenkään peittele lähteitään. Intialaiset numerot esiintyivät islamin kulttuurin piirissä kahtena eri versiona; Eurooppaan päätyivät ns. gobar-numerot, joita käytettiin alueen läntisemmissä osissa. - Vielä nykyäänkin arabian kielessä on käytössä kaksi eri numeromerkkisarjaa, joista pohjoisafrikkalainen on lähempänä meidän käyttämiämme merkintöjä.

Intialaisilla numeroilla laskemista ryhdyttiin Al-Khowarizmin nimen perusteella kutsumaan algorismiksi; algoritmi-sanan nykymerkitys on samaa perua.

Al-Khowarizmin tärkein teos oli Al-jabr wa'l muqabalah. Kirjan nimen ensimmäinen sana, 'jälleenyhdistäminen' tarkoittaa toimenpidettä, jossa yhtälön toiselta puolelta siirretään negatiivinen termi toiselle puolelle ja samalla muutetaan se positiiviseksi (esim. x2=40x- 4x2 $\to$ 5x2=40x). Jälkimmäinen nimen osa tarkoittaa yhtälön eri puolilla olevien positiivisten termien yhdistämistä (esim. 50+x2=29+10x$\to$ 21+x2=10x). Tästä on syntynyt nimi algebra. Al-Khowarizmin oppikirjan pääsisältönä on toisen astjeen yhtälön ratkaiseminen sekä algebrallisesti että geometrisesti. Algebrallinen ratkaisu on olennaisesti sama kuin nykyisin, siis neliöksi täydentäminen ja neliöjuuren otto. Geometrisia ratkaisuja tarvitaan useita sen mukaan, miten (nykymerkinnöin) kertoimien etumerkit jakautuvat. Tyypillisessä tehtävässä x2+10x=39piirretään neliö, jonka sivu on x, sen kullekin sivulle suorakaide, jonka korkeus on $\frac{10}{4}$. Syntyneen ristinmuotoisen kuvion ala on 39. Kun siihen liitetään neljä sivultaan $\frac{10}{4}$ olevaa neliötä, saadaan neliö, jonka ala on 39+25=64 ja jonka sivu on x+5. Mutta tästä nähdään, että x=3. Toisin kuin intialaiset Al-Khowarizmi hyväksyy vain positiiviset juuret. Koko esitys on lisäksi puhtaasti sanallista, Diofantoksen ja Brahmaguptan tuntemia symboliikan alkeita ei käytetä. - Aina 1800-luvulle asti algebralla ymmärrettiin matematiikassa nimen omaan polynomiyhtälöiden ratkaisemista.

Al-Khowarizmin ohella 800-luvun merkittävin matemaatikko oli Thabit-ibn-Qurra (826-901), joka toimitti mm. Eukleideen, Arkhimedeen, Apollonioksen ja Ptolemaioksen tekstien käännöksiä arabiaksi. Käännökset sisälsivät usein Thabitin omia täydennyksiä ja parannuksia. Thabit esitti myös mielenkiintoisen ystävällisten lukuparien konstruktion: jos p, q ja r ovat alkulukuja sekä muotoa $p=3\cdot 2^n-1$, $q=3\cdot 2^{n-1}-1$ ja $r=3^2\cdot 2^{2n-1}-1$, niin 2npq ja 2nr ovat pythagoralaisten mielessä ystävällinen lukupari: kumpikin on toisen tekijöiden summa.

Arabialaiset omaksuivat kreikkalaisesta matematiikasta mieluummin laskennallisia ja käytäntöön liittyviä kuin aksiomaattis-deduktiivisia aineksia. Niinpä geometrian osa-alueista trigonometria kehittyi islamin piirissä pisimmälle, melko lähelle nykymuotoaan. Arabitähtitieteilijät omaksuivat Intiasta sinifunktion ja ottivat itse käyttöön tangenttifunktion. Huomattavin trigonometrian kehittäjä oli Abu'l-Wefa (940-97), joka laski kahdeksan desimaalin tarkkuutta vastaavan sinitaulukon kulmille 15':n välein, tunsi pallotrigonometrian sinilauseen ja käytti jossain määrin kaikkia kuutta trigonometrista funktiota.

Islamin kukoistuskauden viimeiset suuret matemaatikot ovat suuren yleisön keskuudessa runoilijana paremmin tunnettu, Persian Khorasanissa vaikuttanut Omar Khaijjam (1050[?]-1123) (kokoelmat Teltantekijän lauluja ja Viisaan viini on suomennettu; uskonnollisesti Omar oli lähinnä ateisti) ja mongolihallitsija Hulagu-kaanin hoviastronomi Nasir Eddin al-Tusi (1201-74). Omar kirjoitti algebran esityksen, jossa tutkitaan systemaattisesti kolmannen asteen yhtälöitä. Jo Menaikhmos ja Arkhimedes olivat ratkaisseet kartioleikkausten avulla kolmannen asteen yhtälöitä erikoistapauksissa, mutta Omar esitti yleisen geometrisen ratkaisun (tai suuren joukon eri geometrisia ratkaisuja kertoimien eri merkkikombinaatioiden mukaan). Omar ei uskonut, että yleinen kolmannen asteen yhtälö voitaisiin ratkaista algebrallisesti.

Omarin ratkaisu kolmannen asteen yhtälölle x3+b2x+a3=cx2 on seuraava (piirrä kuva!): Määritetään verrannosta $\frac{b}{a}= \frac{a}{ d}$ d ja verrannosta $\frac{b}{d}=\frac{a}{e}$ e. Silloin . Piirretään jana AB=e ja erotetaan suoralta AB jana BC=c. Piirretään B:n kautta kohtisuora AC:tä vastaan ja erotetaan siltä BE=b. Piirretään AC halkaisijana ympyrä, joka leikkaa BE:n pisteessä D. Erotetaan säteeltä BC jana BG siten, että $\frac{ED}{BE}= \frac{AB}{BG}$. Täydennetään DBG suorakaiteeksi DBGH. Piirretään E:n kautta AC:n suuntainen suora, joka leikkaa GH:n pisteessä M. Piste H ja suorat EF ja EM määrittävät hyperbelin, niiden pisteiden P uran, joiden näistä suorista laskettujen etäisyyksien tulo on $DH\cdot MH$. Piirretty puoliympyrä leikkaa tämän hyperbelin pisteessä J. Pisteestä J suoria EM ja AC vastaan piirretty kohtisuora leikkaa EM:n pisteessä K ja suoran AC pisteessä L. Hyperbelin ominaisuuden ja pisteen G valinnan nojalla $EK\cdot KJ=EM\cdot MH=BG\cdot ED=BE\cdot AB$ ja $BL\cdot LJ=EK\cdot (BE+KJ)=EK\cdot BE+BE\cdot AB=BE\cdot AL$. Siis $BL^2\cdot LJ^2=BE^2\cdot AL^2$. Mutta puoliympyrän tunnetun ominaisuuden nojalla $LJ^2=AL\cdot LC$. Siis $BL^2\cdot AL\cdot LC=BE^2\cdot AL^2$ eli $BE^2\cdot AL=BL^2\cdot LC$. Edelleen BE2(BL+AB)=BL2(BC-BL). Mutta tässä olevat janat (paitsi BL) perustuvat kaikki yhtälön kertoimien perusteella tehtyihin valintoihin. On tullut osoitettua, että $b^2\left(BL+\frac{a^3}{ b^2}\right)=BL^2(c-BL)$ eli $BL^3+b^2\cdot BL+a^3=c\cdot BL^2$. Yhtälön ratkaisu on x=BL.

Sekä Omar että Nasir yrittivät vakavasti löytää todistusta Eukleideen viidennelle postulaatille. Nasirin ansioita on lisäksi ensimmäinen astronomiasta irrotettu taso- ja pallotrigonometrian yleisesitys.

Viimeinen mainittava islamilainen matemaatikko on Al-Kashi, joka toimi Samarkandissa 1400-luvun alkupuoliskolla. Al-Kashi oli taitava laskija, jolla oli merkitystä desimaalilukujen käyttööntulolle (vaikka hän itse käytti vielä mielellään - ajan tavan mukaan - seksagesimaalimurtolukuja tarkoissa laskuissa). Al-Kashin laskema $\pi$:n 16-desimaalinen arvo säilyi kauan tarkkuusennätyksenä.


5.3 Kiina

Kiinassa oli käytössä eräänlainen kymmenjärjestelmä jo ajanlaskumme alun aikoihin. Siinä numeroille 1:stä 9:ään oli kullekin kaksi merkkiä, ja kirjoitettaessa joka toinen numero valittiin ensimmäisestä ja joka toinen toisesta sarjasta. Nollasymbolia ei alkuun tunnettu. Negatiivisen ja positiivisen luvun ero oli selvillä jo melko varhain. Positiiviset luvut kirjoitettiin punaisina, negatiiviset mustina.

Jo ajanlaskumme kolmannella vuosisadalla kirjoitetussa teoksessa Jiuzhang suanshu (Laskusäännöt yhdeksässä luvussa), jonka tekijä on Liu Hui, esiintyy usean tuntemattoman lineaarisen yhtälöryhmän ratkaisu eliminointimenetelmällä. Yhtälöiden kertoimet on sijoitettu ''matriisin'' pystyriveiksi, joilla operoidaan samoin kuin matriisin vaakariveillä nykyisin Gaussin eliminoinniksi kutsutussa metodissa.

Myös Kiinassa laskettiin keskiajalla tarkkoja $\pi$:n likiarvoja: Zu Chongzhi (430-501) pääsi tulokseen $3,1415926 < \pi < 3,1415927$. Kiinalaista alkuperää on sittemmin englantilaisen W. G. Hornerin (1786-1837) mukaan nimetty menetelmä algebrallisen yhtälön P(x)=0 likimääräiseksi ratkaisemiseksi: jos x0 on likimääräinen ratkaisu, niin sijoitus x=x0+y johtaa uuteen yhtälöön P1(y)=0, jolla on pieni juuri y; koska y:n korkeammat potenssit ovat pieniä, tälle uudelle yhtälölle voidaan helposti antaa approksimaatio y0 jne. Menetelmän, jonka kiinalainen nimi on fan fa, esitti ainakin Qin Jiushao (noin 1247). Sen laskennollinen toteutus, jonka voi katsoa perustuvan polynomin $x^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots a_1x+a_0$kirjoittamiseen muotoon $x(x(\dots(x+a_{n-1})+a_{n-2})\dots+a_1)+a_0$ on erityisen kätevä. Ratkaistaan likimääräisesti yhtälö

x3+2x2-5x-10=0. Havaitaan, että 2:n ja 3:n välissä on nollakohta. Laskukaavion
1 2 -5 -10
  +2 +8 +6
  4 3 -4
  +2 +12  
  6 15  
  +2    
  8    
avulla saadaan polynomi uuden muuttujan y=x-2 avulla: y3+8y2+15y-4. Tämän polynomin eräs nollakohta on välillä $(0,\,1)$; polynomilla y3+80y2+1500y-4000 on nollakohta välillä $(2,\,3)$. Laskukaavio
1 80 1500 -4000
  +2 +164 +3328
  82 1664 -672
  +2 +168  
  84 1832  
  +2    
  86    
merkitsee, että on tehty uusi sijoitus y=x+2 ja saatu polynomi muotoon x2+86x2+1832x-672. Tämän polynomin likimääräinen juuri on $x=\frac{672}{1832}=0,\!37$. Alkuperäisen yhtälön likimääräisratkaisu on siten $x=2,\!237$. - Koska x3+2x2-5x-10=(x+2)(x2-5), juuren tarkka arvo on $\sqrt{5}\approx 2,\!236$.

Qinin kirjoituksista löytyy myös syvällinen todistus lukuteoriaan kuuluvalle ns. kiinalaiselle jäännöslauseelle: on olemassa luku, jota annetuilla luvuilla jaettaessa saadaan annetut jakojäännökset. Jang Hui (n. 1270) esitti kaavan n:n ensimmäisen neliöluvun summalle ja binomikerroinkaavion, jonka tunnemme Pascalin kolmiona.

Ensimmäiset painetut matemaattiset kirjat ilmestyivät Kiinassa vuoden 1100 paikkeilla. Kiinalaisen osin ilmeisesti hyvin korkeatasoisen matematiikan yhteydet muihin kulttuureihin olivat niukat, eikä Kiinan suoraa vaikutusta matematiikan kehitykselle muualla voi selvästi osoittaa.


5.4 Eurooppa varhaiskeskiajalla

Kreikkalainen traditio säilyi jossakin määrin bysanttilaisen kulttuurin piirissä toiselle vuosituhannelle asti: joitakin kommentaareja ja oppikirjanomaisia esityksiä kirjoitettiin. Länsi-Euroopassa oli matematiikan taso Rooman valtakunnan hajoamisen jälkeen erittäin alhainen. Kreikan kieli, jolla suurin osa antiikin matematiikkaa oli kirjoitettu, oli jokseenkin kokonaan unohdettu. Vaikka Kaarle Suuren aikana (noin 800) tehtiin joitakin yrityksiä koululaitoksen kehittämiseksi, ei matematiikassa ylitetty alkeisaritmetiikan tasoa. Huomattavimmat matemaattiset yritykset koskivat kalenterin liikkuvien juhlapyhien määritystä. Oli toivottavaa, että joka luostarissa olisi ollut yksi kalenterilaskuja taitava munkki. Katolisen kirkon asenne tietoon ja tieteeseen oli muuten pääosin torjuva. Ns. pimeän keskiajan merkittävimpiä matematiikan harrastajia on ranskalaissyntyinen Gerbert (940[?]-1003), sittemmin paavi Sylvester II, joka tiettävästi ensimmäisenä länsimaalaisena käytti intialais-arabialaisia numeroita.

Matematiikan harrastus länsimaissa alkoi jossain määrin elpyä 1100- ja 1200-luvuilla. Tuolloin lännessä ruvettiin omaksumaan islamilaisessa maailmassa tunnettua tietoa ja kääntämään sekä kreikkalaista alkuperää olevia että varsinaisia arabialaisia tekstejä latinaksi. Suoraan kreikasta ei käännetty mitään ennen 1400-lukua. Tietoa suodattui eniten Espanjan kautta; etenkin monikansallinen Toledon kaupunki oli merkittävä portti islamilaisen ja kristillisen maailman välillä. Sotaisten ristiretkien merkitys tiedon siirrossa ei sitä vastoin varmaankaan ole ollut niin suuri kuin usein esitetään.

Ensimmäinen merkittävä matematiikan kääntäjä oli Bathissa Englannissa vaikuttanut Adelard (1075-1160), joka mm. käänsi Eukleideen Alkeet latinaksi. Työteliäin kääntäjä lienee ollut Toledossa työskennellyt Gerard Cremonalainen (1114-87), jonka ainakin 85 nimikettä sisältävä käännöstöiden luettelo sisältää mm. Ptolemaioksen Almagestin ja Al-Khowarizmin kirjoituksia. (Aikaisemmin mainittu sini-väärinkäsitys sattui juuri Gerardille.) Yleensä kiinnostus kohdistui pikemminkin aritmeettis-algebrallisen tradition mukaisiin teoksiin kuin vaikeampaa geometrista perinnettä edustaviin käsikirjoituksiin.


5.5 Fibonacci

Ensimmäinen itsenäisenä matemaatikkona merkittävä länsimaalainen oli Leonardo Pisano eli Fibonacci (1180[?]-1250), jonka kuuluisa teos Liber abbaci (1202; Muoto abaci esiintyy toisissa lähteissä) oli (helmitaulun kaltaiseen abakukseen liittyvästä nimestään huolimatta) ensimmäisiä kymmenjärjestelmän aritmetiikan oppaita. Kymmenjärjestelmän yhtä olennaista piirrettä, murtolukujen desimaalimerkintää, Leonardo ja hänen aikalaisensa eivät oivaltaneet. Vaikeatajuisena pidetty kymmenjärjestelmä herätti vastustusta. Vuonna 1299 Firenzessä annetussa säädöksessä rahanvaihtajia kiellettiin käyttämästä kymmenjärjestelmää.

Vaikka Liber abbacin matemaattinen taso ei kovin korkea olekaan, sen on tehnyt kuolemattomaksi kuuluisa tehtävä:

Kuinka monta kaniiniparia syntyy vuodessa, jos vuoden alussa on yksi pari ja jokainen pari synnyttää joka kuukausi uuden parin, joka alkaa synnyttää kahden kuukauden kuluttua?

Koska tehtävän mukaan tammikuun alussa pareja on 1, helmikuun alussa 2, maaliskuun alussa 3, huhtikuun alussa nämä kolme ja alkuperäisen parin ja tammikuussa synnyttäneen parin jälkeläiset, siis yhteensä 5 jne, nähdään, että parien lukumäärän ilmoittaa palautuskaavaa

an+1 = an + an-1.

Tätä kaavaa, alkuarvoilla a1=a2=1, noudattavaa lukujonoa kutsutaan Fibonaccin jonoksi ja sen jäseniä Fibonaccin luvuiksi. Päättymättömyys oli esillä jo Fibonaccin omassakin ratkaisussa joka numeerisen (377 paria) ratkaisun ohella sisältää maininnan siitä, että prosessia voi jatkaa miten pitkälle tahansa. Fibonaccin jonon lukuisia mielenkiintoisia ominaisuuksia ja sovelluksia tutkitaan yhä, jopa niin, että jonon harrastajilla on oma, vuonna 1963 perustettu yhdistyksensä ja aikakauskirjansa The Fibonacci Quarterly. - Yritteen an=rn avulla huomataan, että Fibonaccin luvut ovat sukua yhtälön r2=r+1 ratkaisuille. Itse asiassa

\begin{displaymath}a_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n- \left(\frac{1-\sqrt{5}}{2}\right)^n\right]. \end{displaymath}

Tämä merkitsee mm., että peräkkäiset Fibonaccin luvut suhtautuvat toisiinsa likimäärin kuten kultaisessa leikkauksessa olevat suureet. - Leonardo tutki myös Diofantoksen yhtälöitä ja esitti kolmannen asteen yhtälöille likiarvoratkaisuja. Kolmannen asteen yhtälön x3+2x2+10x=20 likimääräinen seksagesimaalimuotoinen ratkaisu $x=1;22,7,42,33,4,40=1{,}368808107853\dots$on huomattavan tarkka (tarkempi likiarvo olisi $1{,}368808107821\dots$) ja antaa aiheen olettaa Fibonaccin käytössä olleen jonkin variantin ''Hornerin menetelmästä''. Oivaltava oli myös Fibonaccin tapa laskea peräkkäisten kuutiolukujen summa: koska kaaviossa
1      
3     5    
7     9     11  
13     15     17     19
       
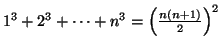n:nnen rivin lukujen keskiarvo on n2ja lukuja on rivillä n kappaletta, kaavion n:n rivin lukujen summa on $1^3+2^3+\dots+n^3$. Toisaalta kuviolukujen ominaisuuksien perusteella nähdään, että k:n ensimmäisen parittoman luvun summa on k2 ja että kaavion n:llä rivillä on $1+2+\dots n=\frac{n(n+1)}{2}$ lukua. Siis $1^3+2^3+\dots+n^3=\left(\frac{n(n+1)}{2}\right)^2$.


5.6 1200- ja 1300-luvut

1200-luvulla Länsi-Euroopan tiede saavutti arabialaisen tason. Perustettiin ensimmäiset yliopistot (Bologna, Pariisi, Oxford, ...), skolastinen filosofia eli huippukauttaan (Albertus Magnus, Tuomas Akvinolainen) ja tekniikka edistyi (ruuti ja kompassi tulivat tunnetuiksi). Matematiikassa tietomäärä lisääntyi ennen muuta käännösten avulla (myös Arkhimedes löydettiin uudelleen), mutta joitakin omaperäisiäkin tuloksia syntyi. Jordanus Nemorarius (n. 1220) käytti kirjaimia numeroiden sijasta algebrassa ja tuli ensimmäisenä esittäneeksi toisen asteen yhtälön ratkaisukaavan yleisessä muodossa:

Olkoon annettu luku abc jaettu osiksi ab ja cja olkoon osien ab ja c tulo d. Olkoon abc:n neliö e ja olkoon fneljä kertaa d ja olkoon g tulos, kun f vähennetään e:stä. Silloin g on ab:n ja c:n erotuksen neliö. Olkoon h g:n neliöjuuri. Silloin h on ab:n ja c:n erotus. Koska htunnetaan, c ja ab ovat määrätyt.

Seuraava vuosisata, kerralla kolmanneksen tai puolet väestöstä vaatineesta mustasta surmasta kuuluisa 1300-luku oli edelleen matemaattisesti köyhää. Merkittävin 1300-luvun matemaatikko lienee ranskalainen Nicole Oresme (1323[?]-82), Lisieux'n piispa Normandiassa. Oresme esitti varsin kehittyneen verranto-opin, jonka yhteydessä hän tuli määritelleeksi (nykykielelle käännettynä) potenssin xq, missä q on rationaaliluku. Koska 43=64 ja 82=64, Oresme näki hyväksi kirjoittaa $8=4^{1\frac{1}{2}}$. Itse asiassa Oresme merkitsi 8:aa symbolilla $1^p\frac{1}{2}\,4$. Oresme - kuten useat muutkin skolastikot - pohti muuttuvia suureita. Suureen muutoksen kuvailemiseksi Oresme otti käyttöön olennaisesti tason koordinaatistoa muistuttavat ''muotojen latitudit ja longitudit''. Muoto oli mikä tahansa suure, joka saattoi muuttua, kuten nopeus, kiihtyvyys tai tiheys, ja muodon latitudi kuvasi sitä määrää, jolla muoto omasi muuttuvaa ominaisuuttaan. Tasaisella nopeudella liikkuvan esineen nopeuden latitudi oli vaakasuora viiva, tasaisesti kiihtyvässä liikkeessä olevan esineen nopeuden latitudi oli nouseva suora. Käsitteet ovat likeistä sukua funktiolle ja sen kuvaajalle. Oresme ei kuitenkaan olennaisesti kyennyt hyödyntämään merkittävää havaintoaan: hän rajoittui lineaarisia funktioita vastaaviin kuvioihin.

Oresme ja hänen englantilainen aikalaisensa Richard Suiseth, joka tunnetaan myös nimellä Calculator (n. 1350) tarkastelivat ja ratkaisivat ongelmia, joissa jouduttiin laskemaan päättymättömien sarjojen summia. (Tosin jo Arkhimedes oli tehnyt samanlaisia päättelyjä.) Oresme jopa totesi harmonisen sarjan

\begin{displaymath}\frac{1}{2} + \frac{1}{3} + \frac{1}{4}+\dots \end{displaymath}

hajaantumisen. Oresme perusti väitteensä sille, että ensimmäinen termi, kahden seuraavan, neljän seuraavan jne., summa on aina ainakin puoli. - Keskiajan skolastikot raivasivat tavallaan tietä myöhemmälle matemaattiselle analyysille äärettömän suuren ja äärettömän pienen olemusta pohtiessaan. Antiikin matematiikalle nämä käsitteet olivat vieraita.

Alkuun - Etusivu - Edellinen - Seuraava

Matematiikkalehti Solmu
2000-09-07