PDF

Ratkaisut geometrisiin tehtäviin

Solmun numerossa 3/1999-2000 esitin kaksi geometrista tehtävää; seuraavassa niiden ratkaisut. Koska geometrian sanallinen selittäminen vie tilaa, jää perustelujen tarkempi analysointi lukijan tehtäväksi.

Molempien ongelmien käsittely perustuu siihen havaintoon, että leikkaamalla pinnat sopivia särmiä pitkin auki saadaan kappale, joka voidaan taivuttaa tasoon ilman, että laatikon pintaa pitkin mitatut etäisyydet vääristyvät.

Oletetaan ensimmäisen tehtävät kohdalla, että pesä sijaitsee ylätahkolla. Geometrisesti on silloin selvää, että suurin etäisyys pesälle saadaan joissakin alatahkon pisteissä. Kyseessä ei kuitenkaan ole alatahkon keskipiste! Jos tilannetta katsotaan alatahkolta käsin ja taivutetaan sopivasti aukileikattu laatikko tasoon, saadaan alla olevan kuvan mukainen tilanne; siinä ylätahkosta on otettu kaksi identtistä kopiota (vasemmanpuoleinen ja ylin suorakulmio), sillä alatahkolta päästään ylätahkon keskipisteeseen neljään eri suuntaan kulkemalla; symmetrian vuoksi riittää tarkastella vain kahta suuntaa.

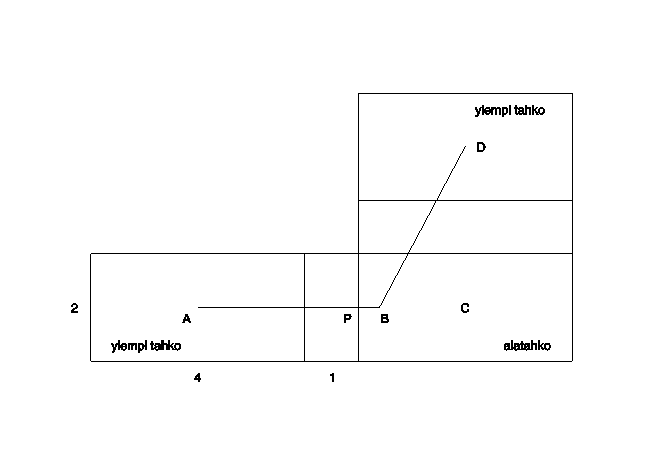
Etäisyyksiä voidaan nyt tutkia tavalliseen tapaan tasossa. Symmetrian perusteella havaitaan, että toinen etsityistä pisteistä (kuviossa B) sijaitsee janalla $\overline{PC}$, ja etäisyyksien $a= \vert\overline{AB}\vert$ sekä $b= \vert\overline{BD}\vert$ täytyy olla samat. Jos merkitään $x= \vert\overline{BC}\vert$, niin a=5-x ja Pythagoraan lauseen nojalla (suorakulmaisesta kolmiosta BCD) on b²=x²+3²=x²+9. Merkitsemällä a=b ja korottamalla tämä yhtälö puolittain toiseen potenssiin, saadaan ratkaistua $x=8/5=1,\! 6$. Löysimme siis kysytyn pisteen; toinen samanlainen on pisteen B peilikuva pisteen C suhteen.

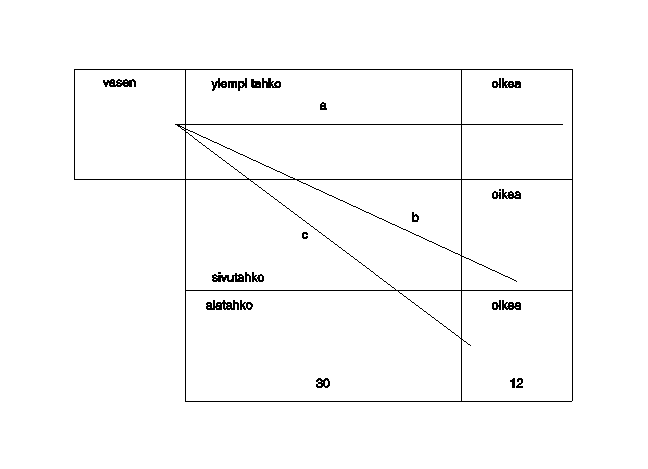
Toista ongelmaa voidaan käsitellä samaan tapaan, mutta tällä kertaa olennaisesti erilaisia kulkusuuntia on kolme. Ratkaisun kannalta tärkeä havainto on se, että eri reittejä kuljettaessa oikealla tahkolla oleva maali sijaitseen tasoon levitettynä eri asemissa. Yläkautta kuljettaessa saadaan matkan pituudeksi a=1+30+11=42, joka on siis hämähäkin reitti menomatkalla. Kulkemalla ylä- ja sivutahkon kautta saadaan etäisyydeksi Pythagoraan lauseen avulla alla olevasta kuviosta $b=\sqrt{(1+30+6)^2+(6+11)^2}=\sqrt{1658}\approx 40,\! 72$. Jos vihdoin kuljetaan sekä ylä-, sivu- että alatahkon kautta, saadaan matkan pituudeksi $c=\sqrt{(1+30+1)^2+(6+12+6)^2}=40$. Alin reitti vastaa siis hämähäkin paluumatkaa, ja se on lyhyin mahdollinen.

Lopuksi kannattaa vielä yrittää havainnollistaa eri vaihtoehdot alkuperäisen särmiön pinnalla.

Pekka Alestalo

Solmu 2/2000-2001
2000-10-31