PDF

Kolmannen asteen yhtälöä ratkaisemassa

Taustana tarinallemme on tämän kevään lyhyen matematiikan yo-tehtävä, jossa käskettiin osoittamaan, että yhtälöllä f(x)=x3-4x-2=0 on juuri välillä (2,3) ja pyydettiin haarukoimaan kyseiselle juurelle kaksidesimaalinen likiarvo. Moni kokelas yritti vahingossa soveltaa probleemaan toisen asteen yhtälön ratkaisukaavaa, toki huonolla seurauksella. Tietystikään tehtävän ratkaisussa ei tarvita juuren tarkan arvon määräämistä - juuren olemassaolo annetulla välillä seuraa polynomifunktion f jatkuvuudesta ja havainnosta f(2)f(3)<0 (merkin vaihtuminen). Mutta meitä motivoikin uteliaisuus: olisihan jännittävää tietää tarkka lauseke kyseiselle juurelle!

Johdamme seuraavassa yleisen ratkaisukaavan kolmannen asteen yhtälölle sekä kerromme lyhyesti asiaan liittyvästä historiasta. Esitiedoiksi riittää lukion pitkän matematiikan kurssi, liitteessä kertaamme lyhyesti kompleksilukujen juurtamista. Myöhemmässä kirjoituksessa tarkoitukseni on käsittelellä hieman yleisemmin likiarvomatematiikkaa, eli kuinka esimerkiksi yllä mainittu juuri voidaan laskea tehokkaasti niin tarkasti kuin halutaan.

1. Reaalijuurten lukumäärä.

Lähdetään liikkeelle yleisestä kolmannen asteen yhtälöstä

a3z3+a2z2+a1z+a0=0,

missä oletamme, että kertoimet ovat mielivaltaisia reaalilukuja ja $a_3\not=0.$Voimme olettaa, että a3=1, koska tähän tilanteeseen päästään jakamalla puolittain luvulla a3. Yhtälö yksinkertaistuu, kun valitsemme uudeksi tuntemattomaksi luvun x asettamalla

z=x-a2/3.

Päädymme yhtälöön (x-a2/3)3+a2(x-a2/3)2+a1(x-a2/3)+a0=0, mikä sieventyy muotoon (tarkista itse välivaiheet!)

 
x3+px+q=0. (1)

Tässä luvuilla p ja q on lausekkeet

\begin{displaymath}p=a_1-{1\over 3}a_2^2,\quad\quad q=a_0-{1\over 3}a_1a_2+{2\over 27}a_2^3. \end{displaymath}

Jos osaamme ratkaista jokaisen muotoa (1) olevan yhtälön, osaamme silloin ratkaista kaikki kolmannen asteen yhtälöt. Johdannossa mainittu yhtälö x3-4x-2=0 onkin jo valmiiksi tätä muotoa. Yhtälön x3+6x2-3x-7=0 juuret saadaan puolestaan lisäämällä luku -2 yhtälön x3-15x+15=0 juuriin. Jatkossa tarkastelemmekin ainoastaan yhtälöä (1).

Lukion kurssissa mainitaan yleinen tieto - algebran peruslause - jonka mukaan n:nnen asteen yhtälöllä on aina tasan n juurta, kun useammankertaiset juuret lasketaan kertalukunsa mukaan ja juuret voivat saada kompleksilukuarvoja. Erityisesti kolmannen asteen yhtälöllä (1) on aina enintään kolme erisuurta juurta.

Merkitään f(x)=x3+px+q. Funktio f on polynomifunktiona jatkuva ja helposti nähdään, että $\lim_{x\to +\infty} f(x)=+\infty$ ja $\lim_{x\to -\infty} f(x)=-\infty$. Koska f vaihtaa merkkiä reaaliakselilla, on sillä oltava ainakin yksi reaalinen nollakohta, olkoon se a. Tiedämme silloin, että polynomi f on jaollinen polynomilla x-a ja voimme kirjoittaa f(x)=(x-a)(x2+dx+e). Toisen asteen yhtälöllä x2+dx+e on tutun ratkaisukaavan mukaan juuret $-d/2\pm \sqrt{(d/2)^2-e}$, jotka joko ovat kumpikin reaalisia tai sitten erisuuria (liitto-)kompleksilukuja. Pätee siis:

Jos yhtälön (1) kaikki juuret ovat reaaliset, niin erisuuria juuria on 1-3 kappaletta. Muussa tapauksessa yksi juurista on reaalinen ja kaksi muuta ovat (ei-reaalisia) liittokompleksilukuja.

Toisen asteen yhtälön x2+bx+c=0 juurten reaalisuuden voimme selvittää ilman että ratkaisemme yhtälöä: riittää pelkästään tarkastella diskriminantin b2-4c merkkiä. Näytämme seuraavassa, että myös kolmannen asteen yhtälölle on olemassa vastaava keino selvittää reaalijuurten lukumäärä. Kun otamme käyttöön hieman differentiaalilaskentaa, ei meidän tarvitse ensin ratkaista kyseistä yhtälöä!

Tarkastellaan tätä varten funktion f derivaattaa f'(x)=3x2+p ja jaetaan käsittely eri tapauksiin luvun p merkin mukaan.

Jos p>0    niin $f'(x)\geq p>0$ kaikilla x, joten f on aidosti kasvava koko reaaliakselilla. Siispä funktiolla $f\colon {\bf R}\to {\bf R}$ on enintään yksi nollakohta ja aiempien havaintojemme nojalla sellainen todella löytyy.

Tapauksessa p<0derivaatalla f'(x)=3x2+p on kaksi erisuurta reaalista nollakohtaa $x=\pm\sqrt{-p/3}.$ Tarkastelemalla derivaatan merkkiä (tee merkkikaavio!) näemme, että f on aidosti kasvava väleillä $(-\infty , -\sqrt{-p/3})$ ja $(\sqrt{-p/3},\infty )$ sekä aidosti vähenevä välillä $(-\sqrt{-p/3},\sqrt{-p/3})$. Erityisesti $f(-\sqrt{-p/3})>f(\sqrt{-p/3})$. Lisäksi totesimme jo aiemmin, että $\lim_{x\to +\infty} f(x)=+\infty$ ja $\lim_{x\to -\infty} f(x)=-\infty$. Jos nyt esimerkiksi kumpikin luvuista $f(\pm\sqrt{-p/3})$ on (aidosti) positiivinen, niin f vaihtaa merkkiä ainoastaan välillä $(-\infty , -\sqrt{-p/3})$, jolloin voimme aiemman nojalla päätellä, että f:llä on täsmälleen yksi nollakohta välillä $(-\infty , -\sqrt{-p/3})$ ja muita nollakohtia ei ole (piirrä hahmotelma kuvaajasta tarkan päättelysi tueksi). Vastaavasti reaalijuuria on vain yksi, jos luvut $f(\pm\sqrt{-p/3})$ ovat negatiivisia. Jos taas luvut $f(\pm\sqrt{-p/3})$ ovat eri merkkisiä, näemme että f:n kuvaaja leikkaa reaaliakselin kerran jokaisella yllä käsittellyistä kolmesta välistä, joten tässä tapauksessa nollakohtia on kolme.

Tarkastellaan vielä vaihtoehtoa, jossa jompi kumpi luvuista $f(\pm\sqrt{-p/3})$ on nolla. Kyseisessä tilanteessa kuvaaja sivuaa reaaliakselia vastaavassa kohdassa, jolloin päättelemme, että yhtälöllä (1) on kaksi reaalista juurta (aiemman mukaan myös kolmas juuri on reaalinen, joten nyt yhtälöllä on kaksoisjuuri).


 
Kuva 1: Kolme eri vaihtoehtoa tapauksessa p<0.
[jpeg-kuva]

Havaintomme voidaan kiteyttää yksinkertaisesti: kun p<0, on reaalijuuria maksimimäärä vain jos luvut $f(\pm\sqrt{-p/3})$ ovat eri merkkiset, eli niiden tulo on negatiivinen. Lasketaan

$\displaystyle f(-\sqrt{-p/3})f(\sqrt{-p/3})$ = $\displaystyle \left( -\sqrt{-p/3}(-p/3)+ p(-\sqrt{-p/3})+q\right) \left(\sqrt{-p/3}(-p/3)+ p\sqrt{-p/3}+q\right)$  
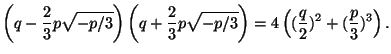  = $\displaystyle \left( q-{2\over 3}p\sqrt{-p/3}\right) \left( q+{2\over 3}p\sqrt{-p/3} \right) =4\left( ({q\over 2})^2+({p\over 3})^3\right) .$  

Otetaan käyttöön merkintä (huomaa miinus-merkki!)

\begin{displaymath}D=-\left (({q\over 2})^2+({p\over 3})^3\right) = -\left ({q^2\over 4}+{p^3\over 27}\right). \end{displaymath}

Lukua D sanotaan yhtälön (1) diskriminantiksi, ja olemme juuri näyttäneet, että (ainakin tapauksessa p<0) se näyttelee samanlaista roolia kuin toisen asteen yhtälön diskriminantti. Nimittäin, edellä tekemiemme havaintojen mukaan yhtälöllä (1) on kolme juurta jos D>0, kaksi juurta jos D=0 ja vain yksi reaalijuuri jos D<0.

Tutkitaan lopuksi, miten edellä johdettu diskriminanttiehto toimii tapauksessa $p\geq 0$. Jos p>0, niin aikaisemman mukaan reaalijuuria on yksi ja toisaalta myös D<0, koska aina $q^2\geq 0$ ja siis $D\leq -p^3/27.$ Tapauksessa p=0 yhtälö saa muodon x3=q, jolla on yksi reaalijuuri ja kaksi (aitoa) kompleksijuurta, jos $q\not=0$, jolloin myös D<0. Jos q=0, niin yhtälöllä on yksi (kolmois)juuri x=0. Jälkimmäinen vaihtoehto vastaa tapausta D=p=0.


Voimme koota tuloksemme seuraavasti:

Lause 1.     Jos diskriminantti on positiivinen, eli D>0, on reaalikertoimisella yhtälöllä (1) kolme keskenään erisuurta reaalijuurta. Jos D<0, on reaalijuuria yksi, ja lisäksi yhtälöllä on kaksi (aitoa) kompleksijuurta, jotka ovat toistensa liittolukuja. Tapauksessa D=0 yhtälön juuret ovat reaaliset, ja niitä on kaksi erisuurta jos lisäksi $p\not=0$, ja ainoastaan yksi (kolmoisjuuri) jos lisäksi p=0.

ESIMERKKI.     Ylioppilastehtävän yhtälölle x3-4x-2=0 saamme $D=-((-{2\over 2})^2+(-{4\over 3})^3)={37\over 27}>0,$ joten sillä on kolme erisuurta reaalijuurta.

HARJ. 1.    Montako reaalijuurta on yhtälöllä x3+3x2-5x-7=0? Entä yhtälöllä x3-300x+1000=0?

HARJ. 2.    Olkoot luvut x1,x2,x3 yhtälön x3+rx2+px+q=0 juuret. Osoita, että r=-(x1+x2+x3), p= x1x2+x2x3+x3x1 ja q=-x1x2x3.Muodosta kolmannen asteen yhtälö, jonka juurina ovat luvut -3, 2 ja 7.

HARJ. 3.    Tiedämme että luvut u,v ovat muotoa x3+px+q=0 olevan yhtälön juuria. Voitko päätellä kolmannen juuren, vaikket tiedäkään lukuja p ja q? Sama kysymys, jos yhtälö on muotoa x3+rx2+q=0.

2. Ratkaisukaava.

Ratkaisukaavan löytäminen kolmannen asteen yhtälölle ei ole lainkaan niin helppoa kuin toisen asteen yhtälölle. Ottaen huomioon algebrallisten merkintöjen puutteellisuuden ei olekaan ihme, ettei sitä keksitty ennen 1500-lukua. Luonnollinen ajatus olisi yrittää täydentää yhtälön (1) vasen puoli kuutioksi, mutta tämä lähestymistapa ei sellaisenaan toimi. Eteenpäin pääsemiseen tarvitaan uusi idea. Sellaisen tarjoaa sijoitus

x=u+v.

Yhtälö (1) saa sievennysten jälkeen muodon (tarkista se)

(u3+v3 +q)+ (3uv +p)(u+v)=0.

Selvästikin tämä yhtälö toteutuu mikäli u ja v toteuttavat yhtälöparin

 \begin{displaymath} \left\{\begin{array}{rl} u^3+v^3&=-q\\ uv&=-p/3. \end{array}\right. \end{displaymath} (2)

Korottamalla jälkimmäisen yhtälön kolmanteen potenssiin saamme yhtälön

 
u3 v3=-(p/3)3. (3)

Siispä tiedämme mitä ovat lukujen u3 ja v3 summa ja tulo. Toisen asteen yhtälön teoriasta (sievennä (y-u3)(y-v3)) tiedämme silloin, että luvut u3 ja v3toteuttavat toisen asteen yhtälön

y2 +qy-(p/3)3,

jota kutsutaan yhtälöä (1) vastaavaksi resolventtiyhtälöksi. Tämän osaamme ratkaista tutulla ratkaisukaavalla ja saamme

\begin{displaymath}u^3=-q/2 +\sqrt{(q/2)^2+(p/3)^3}=-q/2+\sqrt{-D}, \end{displaymath}

missä D=-(q/2)2-(p/3)3 on yhtälön diskriminantti. Vastaavasti

\begin{displaymath}v^3=-q/2-\sqrt{-D}. \end{displaymath}

Toki edellä u ja v ovat symmetrisessä asemassa, eli merkit saattaisivat olla toisinkin päin. Tässä vaiheessa tiedämme, että ratkaisemamme luvut u3,v3 toteuttavat yhtälöparin (2), jossa jälkimmäinen yhtälö on korvattu yhtälöllä (3).

Olkoon sitten $u_0=\root 3 \of {-q/2+\sqrt{-D}}$ (mikä tahansa kuutiojuuren arvo kelpaa tässä). Tämän jälkeen valitsemme kuutiojuuren $v_0=\root 3 \of {-q/2-\sqrt{-D}}$ arvon niin, että yhtälöparin (2) jälkimmäinen yhtälö toteutuu, eli u0v0=-p/3. Tämä on mahdollista, koska suoraan laskemalla voimme tarkistaa, että valinta v0=-p/3u0 toimii, tapauksen u0=0 ollessa yksinkertainen. Silloin pari (u0,v0) selvästikin toteuttaa yhtälöparin (2) ja siis u0+v0 on yhtälön (1) ratkaisu. Olemme selättäneet kolmannen asteen yhtälön!

Yhtälön muiden juurien löytämiseksi merkitsemme $\rho=-1/2+i\sqrt{3}/2$, jolloin siis pätee $\rho^3=1$; vrt. Liite lopussa. Havaitsemme suoraan laskemalla että myös lukuparit $(\rho u_0,\rho^2v_0)$ ja $(\rho^2u_0,\rho v_0)$ toteuttavat yhtälöparin (2). Etsimämme RATKAISUKAAVA saa muodon:

Lause 2.     Merkitään D=-(q/2)2-(p/3)3 ja $\rho=-1/2+i\sqrt{3}/2$. Yhtälön (1) juuret ovat luvut

\begin{displaymath}u_0+v_0,\quad \rho u_0+\rho^2v_0\quad {\rm ja} \quad \rho^2u_0+\rho v_0, \end{displaymath}

missä $u_0=\root 3 \of {-q/2+\sqrt{-D}}$, $v_0=\root 3 \of {-q/2-\sqrt{-D}}$ja kuutiojuuren valinnat on tehty niin, että yhtälö u0v0=-p/3 toteutuu.

Johtamamme ratkaisukaavat tunnetaan CARDANON KAAVOJEN nimellä, koska ne julkaistiin ensimmäisen kerran vuonna 1545 Geronimo Cardanon teoksessa Ars magna.

HARJ. 4.    Edellinen päättely ei vielä näytä, että nämä kaavat antavat kaikki juuret. Tämän todistamiseksi sievennä lauseke $(x-(u_0+v_0))(x-(\rho u_0+\rho^2v_0)) (x-(\rho^2u_0+\rho v_0)),$ ja osoita että saat alkuperäisen yhtälön (1) vasemman puolen.

ESIMERKKI.    Testataksemme johtamaamme ratkaisukaavaa tarkastelemme yksinkertaista yhtälöä x3+x=0. Koska x3+x=x(x2+1)=x(x+i)(x-i),ovat juuret $0, \pm i.$ Nyt D=-1/27 ja voimme valita $u_0={\root 3 \of {\sqrt{1/27}}}=1/\sqrt{3}$, missä siis valitsemme kuutiojuurelle reaalisen arvon. Silloin $v_0=-1/3u_0=-1/\sqrt{3}$, joten u0+v0=0, ja muut kaksi juurta saavat muodon

\begin{displaymath}{1\over \sqrt{3}}\left( (-{1/2}\pm i\sqrt{3}/2)- (-{1/2}\mp i\sqrt{3}/2)\right). \end{displaymath}

Sievennysten jälkeen lauseke tuottaa luvut $\pm i,$ kuten pitääkin.

HARJ. 5.    Ratkaise yhtälöt x3+63x=316 ja x3-4x2+6x-4=0.

HARJ. 6.    Todista yllättävä yhtäsuuruus

\begin{displaymath}{\root 3 \of {\sqrt{5}+2}}-{\root 3 \of {\sqrt{5}-2}}=1 \end{displaymath}

osoittamalla, että vasen puoli toteuttaa kolmannen asteen yhtälön, jonka ainoa reaalijuuri on 1. Keksi itse lisää vastaavia identiteettejä.

3. Casus irreducibilis: trigonometria astuu näyttämölle.

Oletetaan nyt, että ylioppilaskokelas tuntee ratkaisukaavan ja soveltaa sitä em. tehtävään ja ratkaisee yhtälön x3-4x-2=0. Hän laskee ensin $D=-(-{2\over 2})^2- (-{4\over 3})^3=37/27$, ja pränttää sitten sumeilematta paperille kaavan

\begin{displaymath}x=\root 3 \of {1+\sqrt{-37/27}}+\root 3 \of {1-\sqrt{-37/27}}. \end{displaymath}

Saattaa siinä kokeen tarkastajalta tipahtaa punakynä kädestä! Mutta sormi menisi helposti suuhun kokelaaltakin. Kaavathan vaativat ottamaan kolmannen juuren aidosta kompleksiluvusta, ja tämä osoittautuukin erikoislaatuisella tavalla hankalaksi tehtäväksi. Voidaan nimittäin osoittaa, ettei kyseisiä kolmansia juuria yleisessä tapauksessa voida lausua lausekkeina pelkästään reaalisista juurroksista!

Yhtälön (1) kohdalla tapaus D>0, joka siis johtaa kompleksilukujen kuutiojuuriin, tunnetaan nimellä casus irreducibilis ("jakautumaton tapaus"). Casus irreducibilis jäi varsin mystiseksi Cardanolle ja hänen aikalaisilleen, varsinkin kun etukäteen olisi luultavaa, että juuri tapaus D>0, jolloin yhtälöllä on kolme eri suurta reaalijuurta, olisi helpompi kuin tapaus, jossa osa juurista on kompleksisia.

Liiteessä on näytetty, kuinka de Moivren kaavan avulla kompleksiluvusta voidaan ottaa kolmas juuri trigonometristen funktioiden avulla ja Cardanon kaavat säilyvät sikäli käyttökelpoisina. Osoitamme kuitenkin seuraavassa, kuinka tapauksessa D>0 voidaan yhtälö (1) ratkaista suoraan trigonometristen funktioiden yhteenlaskukaavan avulla ilman Cardanon kaavoja!

Nyt p<0 ja voimme tehdä yhtälössä (1) sijoituksen $x=2y\sqrt{-p/3},$jolloin se saa muodon

\begin{displaymath}4y^3-3y=q', \quad \mbox{\rm miss\uml a} \quad q'={q/2\over (-p/3)^{3/2}}. \end{displaymath}

Palautamme mieleen kolminkertaisen kulman kosinin kaavan: koska $\cos(2x)=2\cos^2x-1$ ja $\sin (2x)=2\sin x \cos x$, saamme kosinin yhteenlaskukaavan avulla
$\displaystyle \cos(3x)$ = $\displaystyle \cos (x+2x)=\cos x(2\cos^2 x-1)- \sin x(2\sin x\cos x)$  
  = $\displaystyle 4\cos^3 x-3\cos x,$ (4)

missä käytimme tietoa $\sin^2 x=1-\cos^2 x.$Sijoitamme lisäksi $y=\cos (t)$ ja $q'=\cos(\phi ) ,$ missä $\phi=\overline{\rm arc}{\rm cos} (q').$ Jälkimmäinen sijoitus on mahdollinen, sillä tapauksessa D>0 on välttämättä |q'|<1. Tällöin myös |y|<1, sillä tapauksessa $\vert y\vert\geq 1$ on lausekkeen 4y3-3y itseisarvo vähintään 1.

Suorittamalla viimeiset sijoitukset yhtälö saa muodon $ 4\cos^3 (t)- 3\cos (t)=\cos(\phi), $ mikä yhteenlaskukaavan nojalla on yhtäpitävä yksinkertaisen yhtälön

\begin{displaymath}\cos (3t)=\cos (\phi) \end{displaymath}

kanssa. Pienen laskun jälkeen näemme, että tämän yhtälön ratkaisuiksi (mod $2\pi$) soveltuvat luvut

\begin{displaymath}t\in\{ \pm\phi/3, \pm(\phi/3+2\pi/3), \pm(\phi/3+4\pi/3)\} . \end{displaymath}

Kun näistä otetaan kosinit, ei merkillä ole väliä, joten puolet vaihtoehdoista tippuu pois. Siispä:

Lause 3.     Jos D>0, niin yhtälön (1) juuret ovat luvut

\begin{displaymath}2\sqrt{p\over3}\cos ({\phi\over 3}),\quad 2\sqrt{p\over3}\co... ...m ja} \quad 2\sqrt{p\over3}\cos({\phi\over 3}+{4\pi\over 3}), \end{displaymath}

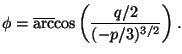
missä $\phi=\overline{\rm arc}{\rm cos} \left( {\displaystyle{q/2\over (-p/3)^{3/2}}}\right) .$

Selvästi saadut juuret ovat kaikki erisuuret. Yllättäen tarvitsimmekin trigonometriset funktiot avuksi algebrallisen yhtälön ratkaisemisessa!

HARJ. 7.    Tarkastele tapausta jossa diskriminantti häviää, D=0. Näytä, että Cardanon kaavoissa voidaan valita $u_0=v_0={\root 3 \of {-q/2}} = -{\root 3 \of {q/2}}$, joten yksi juuri on $-2{\root 3 \of {q/2}}$, ja totea, että muut kaksi juurta yhtyvät koska $\rho^2+\rho=-1$, ja että niiden arvo on ${\root 3 \of {-q/2}}$.

Yhteenvetona kertaamme vielä:

Tapauksessa D>0 on erisuuria reaalijuuria kolme ja ratkaisu on mahdollista esittää trignometristen funktioiden avulla reaalisessa muodossa. Tapauksessa D<0 reaalijuuria on yksi ja se saadaan suoraan Cardanon kaavojen avulla reaalisilla juurroksilla, lisäksi kompleksijuuret saadaan kyseisistä juurroksista kertomalla sopivasti luvuilla $-{1/2}\pm i\sqrt{3}/2$. Jos diskriminantti on nolla, niin juuret ovat reaaliset ja osa niistä yhtyy.

Voidaan osoittaa, että Cardanon kaavat ovat voimassa, vaikka yhtälön kertoimet olisivat kompleksilukuja. Jopa tässä osiossa johtamamme kaavat pätevät yleisesti, kun ne tulkitaan oikein - tällöin joudutaan laskemaan trigonometrisia funktioita kompleksilukuarvoilla, mikä olisi mielenkiintoisen tarinan aihe sinänsä.

ESIMERKKI.    Tarkastellaan yhtälöä x3-x=0, jonka ratkaisuiksi havaitaan helposti luvut $0, \pm 1.$ Nyt q'=0, eli voimme valita $\phi=\pi/2$ ja siis $\phi/3=\pi /6 .$ Lisäksi $2\sqrt{-p/3}=2/\sqrt{3}$ ja juuret saavat muodon $2\cos (t)/\sqrt{3}$, missä $t\in \{ \pi/6, 5\pi/6, 3\pi/2\}$, eli saamme täsmälleen oikeat luvut.

HARJ. 8.     Ratkaise yhtälö x3-63x=162. Keksi itse lisää esimerkkejä ja testaa laskimella saamiasi juuria.

HARJ. 9.    Totea vihdoin, että ylioppilaskirjoitustehtävän yhtälön x3 -4x-2=0 välillä (2,3) oleva juuri voidaan kirjoittaa muotoon

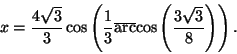
\begin{displaymath}x= {4\sqrt{3}\over 3}\cos \left( {1\over 3}\overline{\rm arc}{\rm cos} \left( {3\sqrt{3}\over 8}\right) \right) . \end{displaymath}

Mitkä ovat yhtälön muut juuret?

4. Historiaa.

Kolmannen asteen yhtälön ratkaisutarina on kiehtova pala matematiikan historiaa. Jo antiikin kreikkalaiset kohtasivat kolmannen asteen yhtälöitä, koskapa monet aikakauden keskeiset ongelmat kuten kuution kahdennus tai kulman kolmiajako johtavat sellaiseen. Arkhimedes kykeni esittämään geometrisen ratkaisun, joka väistämättä johti konstruktioon, jota ei voi suorittaa pelkästään harppia ja viivotinta käyttäen. Geometrisen ratkaisun esittivät myös eräät muut matemaatikot kuten kuuluisa runoilija-matemaatikko Omar Khayam 1200-luvulla.

Algebrallinen ratkaisu kolmannen asteen yhtälölle keksittiin lopulta 1500-luvulla. Muotoa (1) olevan yhtälön ratkaisun löysi noin v. 1515 Scipione del Ferro (1465-1526), matematiikan professori Bolognan yliopistossa. Pidetään mahdollisena, että hän olisi saanut ratkaisevan idean vanhemmista arabialaisista lähteistä. Ferro ei julkaissut tulosta, mutta paljasti suuren salaisuutensa oppilaalleen Antonio Maria Fiorille. Noin vuonna 1535 matemaatikko Niccolo Fontana alias Tartaglia löysi ilmeisestikin itsenäisesti ratkaisun yhtälölle, joka on muotoa x3+rx2+q=0. Fior haastoi Tartaglian julkiseen kaksintaisteluun kolmannen asteen yhtälöiden ratkaisemisessa, aseenaan Ferron ratkaisukaava. Kumpikin osallistuja asetti toisen ratkaistavaksi tukun yhtälöitä. Päivää ennen määräaikaa yötä päivää uurastanut Tartaglia lopulta löysi ratkaisukeinon myös Fiorin edustamalle yhtälötyypille. Lopputuloksena oli, että Tartaglia ratkaisi kaikki hänelle annetut tehtävät, Fior ei ainuttakaan.

Voitokas Tartaglia halusi puolestaan pitää maineensa avaimet omana tietonaan ja päätti olla paljastamatta ratkaisuaan muille kunnes ehtisi julkaista sen kirjan muodossa. Monitieteilijä Geronimo Cardano sai kuitenkin houkuteltua Tartaglian paljastamaan ratkaisukaavan itselleen, tosin ensin runomuotoon puettuna! Tähän liittyi vakuutus olla paljastamatta salaisuutta. Lupauksestaan huolimatta Cardano julkaisi Tartaglian tulokset suuressa teoksessaan Ars Magna (Suuri Taide/Tiede). Lisäksi hän sisällytti tähän teokseen neljännen asteen yhtälön ratkaisun, jonka oli keksinyt hänen lahjakas oppilaansa Ludovico Ferrari (1522-1565).

On ymmärrettävää, että Tartaglia oli katkera Cardanolle, ja tilanteesta kehkeytyikin matematiikan historian ensimmäisiä tunnettuja prioriteettikiistoja. Käydyssä kiistassa Ferrari puolusti kiihkeästi opettajaansa. Cardanon ja Ferrarin hyväksi on luettava se seikka, että he saivat käsiinsä myös Fiorin alkuperäisen ratkaisun Fiorin vävyltä. Cardanon kunniaksi on myös sanottava, että hän ei väittänyt keksineensä itse ratkaisukaavoja, vaan tunnusti tässä suhteessa täysin muiden ansiot.

Kolmannen asteen yhtälön ratkaiseminen oli suuri läpimurto algebrassa, joka toi tekijöilleen kuuluisuutta. Tuona hetkenä eurooppalainen matematiikka ylitti antiikin saavutukset. Kaavojen käytännöllinen arvo on huomattavasti vähäisempi (toisen asteen yhtälön ratkaisukaava sen sijaan on matematiikan perustyökaluja) kuin itse ratkaisemisen periaatteellinen ja psykologinen merkitys.

Lisäksi on merkittävää, että Cardanon kaavojen löytäminen johti kompleksilukujen keksimiseen: erityisesti edellä tarkasteltu casus irreducibilis näytti, että puhtaasti reaalisten ilmiöiden käsittelyyn tarvitaan kompleksilukuja. Jo Cardano laski formaalisti imaginääriluvuilla, vaikkei hän hyväksynytkään niitä oikeasti olemassa oleviksi suureiksi. Teoksessa Ars Magna hän laskee formaalisti tulon $(5+\sqrt{-15})(5-\sqrt{-15})$saaden tulokseksi korrektisti 40. Mahdollisesti Cardono harrastaa tässä yhteydessä sanaleikkiä, sillä hän mainitsee kyseisestä laskutoimituksesta dimissis incruciationibus, jonka voi kääntää "unohtaen henkiset kärsimykset" tai yhtä hyvin "ristitulojen supistuttua pois" (vrt. viite [C], s. 238).

Italialainen Rafael Bombelli (1526-1573) ymmärsi, että Cardanon kaavat toimivat myös casus irreducibilisin kohdalla; hän itse kuvasi oivallustaan "villiksi ajatukseksi." François Viete (1540-1603) keksi yllä esittämämme trigonometrisen ratkaisun kyseiselle tapaukselle. Tarkasteltavana ajanjaksona huomattavaa kehitystä tapahtui myös matematiikan symbolisessa esityksessä: Cardano muotoili algebralliset kaavat sanallisessa muodossa, mikä nykykatsannossa raskauttaa suuressa määrin esityksen ymmärtämistä. Viete puolestaan sovelsi symboleita tavalla, joka jo jossain määrin lähentelee nykyaikaista merkitsemistapaa.

GERONIMO CARDANO (1501-1576) syntyi Paviassa Italiassa. Hän oli aikakautensa tunnetuimpia lääkäreitä ja toimi huomattavissa yliopistollisissa viroissa Paviassa ja Bolognassa. Myös keksijänä Cardanon nimi on säilynyt: voimansiirron perusrakenne kardaaniakseli on nimetty hänen mukaansa. Matemaatikkona hänet tunnetaan ennen muuta merkittävästä teoksestaan Ars Magna [GC], joka kokosi yhteen tunnetun algebran ja nosti sen uudelle tasolle kolmannen ja neljännen asteen yhtälöiden ratkaisukaavojen myötä. Lisäksi teoksessa sallitaan negatiiviset (Cardanon kielessä "kuvitellut") ratkaisut yhtälöille ja myös viitataan imaginääristen ratkaisujen mahdollisuuteen. Monipuolisuuden puutteesta Cardanoa ei voi syyttää: eräässä vaiheessa hänet tuomittiin jumalanpilkasta, myöhemmin hän kuitenkin toimi Roomassa paavin hoviastrologina. Elämä oli tuohon aikaan värikkäämpää kuin "Kauniissa ja rohkeissa" tänään: Cardanon vanhempi poika surmasi oman vaimonsa arsenikilla, Cardanon oppilaan Ferrarin puolestaan myrkytti hänen oma sisarensa.

NICCOLO FONTANA alias TARTAGLIA (1499-1557) syntyi Bresciassa Italiassa. Hän sai melkein surmansa miekaniskusta ranskalaisten sotilaiden vallatessa Brescian v. 1512. Tartaglia parani (tarinan mukaan hänen äitinsä pelasti poikansa matkimalla koiran tapaa hoitaa haavoja: nuolemalla ne säännöllisesti!), mutta kärsi tapahtuneen johdosta vakavasta änkytyksestä loppuikänsä, mistä lempinimi Tartaglia (änkyttäjä) juontaa juurensa. Köyhyyden vuoksi Tartaglia joutui opettelemaan kirjoittamista yksin käyttäen salaa kirjoitusalustana läheisen hautausmaan hautakiviä! Tartaglia opetti matematiikkaa useissa Italian kaupungeissa. Kolmannen asteen yhtälöiden lisäksi hän teki pioneeritutkimussa muun muassa ballistiikassa.

Viitteet.

Esitetty ratkaisukaavan johto seuraa Kalle Väisälän mainiota teosta [V, 81§], josta myös löytyy (82§) neljännen asteen yhtälön ratkaisukaava sekä todistus sille, että viidennen tai korkeamman asteen yhtälöille ei ole olemassa yleistä ratkaisukaavaa. Matematiikan historian erinomainen yleisesitys [B] sekä erikoistuneempi lähdeteos [E] sisältävät lisää tietoa kolmannen asteen yhtälöön liittyvästä historiasta.

[B] Carl Boyer: Tieteiden kuningatar I-II. Art House, 1994.

[C] Ronald Calinger: Classics of mathematics. Moore Publishing Company, 1982.

[GC] Geronimo Cardano: The great art (Ars magnae), 1545.

[E] Howard Eves: Great moments in mathematics (before 1650). The Mathematical Association of America, 1980.

[V] Kalle Väisälä: Lukuteorian ja korkeamman algebran alkeet. Otava, (toinen painos) 1961.

Liite: Juurenotto ja toisen asteen yhtälö kompleksiluvuille.

Palautamme mieleen, että mielivaltainen kompleksiluku z voidaan kirjoittaa muotoon z=a+ib, missä a ja b ovat mielivaltaisia reaalilukuja ja i on niin sanottu imaginääriyksikkö, joka toteuttaa yhtälön i2=1. Luku a on luvun z reaaliosa ja b imaginääriosa. Luvun z konjugaattiluku on a-ib.Luku ja sen konjugaatti ovat keskenään liittokompleksilukuja - tästä esimerkkinä luvut $1\pm i.$

Kompleksiluvuilla harrastetaan algebrallisia laskutoimituksia (ja monia muitakin) aivan kuin tavallisilla luvuilla; lisäksi termit i2 voidaan aina sieventää luvuksi -1. Esimerkiksi

(a+ib)(c+id)=ac+adi+bci+ bdi2=ac-bd+(ad+bc)i.

Toisen asteen reaalikertoimiselle (itse asiassa jopa kompleksikertoimiselle) yhtälölle x2+bx+c=0 juuret saadaan tavallisesta ratkaisukaavasta: jos diskriminantti D=b2-4c on negatiivinen, saavat juuret muodon $(-b\pm i\sqrt{-D})/2.$

HARJ. 10.    Osoita että toisen asteen yhtälön x2+bx+c=0 juurten summa on -b ja tulo c vaikka juuret olisivat kompleksiset. Testaa tämä osoittamalla ratkaisukaavaa käyttäen, että yhtälön x2-6x+13=0 juuret ovat luvut $3\pm 2i$. Tarkista juuret myös suoraan yhtälöön sijoittamalla.

Algebran peruslauseen mukaan yhtälöllä zn=w, missä w on kompleksiluku, on tasan n juurta. Tapauksessa n=2juurten (siis luvun a neliöjuuren) laskeminen ekplisiittisessä muodossa reaalisilla juurilausekkeilla luvun w reaali- ja imaginääriosista on mahdollista (vrt. harj. 13 alla). Kun $n\geq 3$, tämä ei ole yleisesti totta. Juuret voidaan kuitenkin helposti laskea käyttämällä kompleksiluvuille polaariesitystä:

\begin{displaymath}z=x+iy=r(\cos\theta +i\sin\theta ), \end{displaymath}

missä $r=\sqrt{x^2+y^2}$ on luvun w moduli ja $\theta\in\real $ on vaihekulma. Luku $r\geq 0$ on yksikäsitteisesti määrätty ja $\theta $ on yksikäsitteinen modulo $2\pi .$ Vaihekulma voidaan ratkaista vaikkapa yhtälöstä $\tan (\theta)=y/x$, missä ratkaisuista on valittava ne jotka antavat oikeat merkit trigonometrisille funktioille $\cos\theta$ ja $\sin\theta$.

DE MOIVREN KAAVA sanoo, että

\begin{displaymath}z^n=r^n(\cos (n\theta) +i\sin (n\theta)), \end{displaymath}

eli korotettaessa potenssiin n moduli korotetaan vastaavaan potenssiin ja vaihekulma kerrotaan n:llä. de Moivren kaavan avulla voimme helposti ottaa kompleksiluvusta w n:nnen juuren kirjoittamalla sille ensin polaariesityksen $w=R(\cos\phi +i\sin\phi )$, jolloin näemme että juurella $z=\root n\of w$ on n eri arvoa (kun $w\not=0$)

\begin{displaymath}z={\root n \of {R}}\left( \cos ({\phi\over n} +{k2\pi \over n... ...phi\over n} +{k2\pi \over n})\right) ,\quad k=0,\ldots , n-1 . \end{displaymath}

ESIM.     Kun nyt osaamme ottaa juuria myös kompleksiluvuista (tosin trigonometrian avulla), tutkimme miten Cardanon kaavat toimivat yhtälölle. x3-x=0, jonka juuret ovat $0, \pm 1$ (kyseessä on casus irreducibilis). Cardanon kaavat antavat yhdeksi juureksi luvun

\begin{displaymath}x={\root 3 \of {\sqrt{-1/27}}}+{\root 3 \of {-\sqrt{-1/27}}}=... ...-1}}})= {1\over \sqrt{3}} ({\root 3 \of i}+{\root 3 \of {-i}}) \end{displaymath}

Luvun ${\root 3 \of i}$ määrittämiseksi kirjoitamme $i=\cos (\pi /2)+i\sin (\pi /2)$, jolloin saamme kuutiojuurelle arvot $\cos \phi +i\sin\phi$, missä $\phi\in\{ \pi /6 ,\pi /6+2\pi /3, \pi /6+4\pi /3\}$. Kyseisten kulmien trigonometriset funktiot osaamme laskea tarkasti ja päädymme lukuihin $i, \ (\pm \sqrt{3} + i)/2$. Vastaavasti laskemme että juuri ${\root 3 \of -i}$ saa arvot $-i, \ (\pm \sqrt{3} -i)/2$. Cardanon kaavoissa voimme vaikkapa valita $u_0=i/\sqrt{3}$ ja $v_0=-i/\sqrt{3}$, jolloin myös ehto u0v0=-(-1/3) toteutuu. Summa u0+v0=0 antaa yhden juuren, tarkista itse että kaavat antavat oikein muut juuret.

HARJ. 11.    Ratkaise yhtälö z3=1. (Vihje: voit joko käyttää de Moivren kaavaa tai sitten kirjoittaa z3-1=(z-1)(z2+z+1) ja ratkaista toisen asteen yhtälön z2+z+1=0 ratkaisukaavalla)

HARJ. 12.     Jos luku z on luvun w kuutiojuuri, näytä että muut juuret ovat $\rho z, \rho^2z$, missä $\rho=(-1+i\sqrt{3})/2$.

HARJ. 13.    Osoita, että neliöjuuri kompleksiluvusta w=u+iv (tässä u,v ovat reaalilukuja) voidaan lausua eksplisiittisesti reaalisten juurrosten avulla. Merkitse (x+iy)2=u+iv ja totea, että reaaliluvut x ja ytoteuttavat yhtälöparin x2-y2=u,     2xy=v . Ratkaise tämä korottamalla jälkimmäinen yhtälö neliöön, jolloin saat selville lukujen x2 ja -y2 summan ja tulon, eli voit kirjoittaa toisen asteen yhtälön, jonka nämä luvut toteuttavat.

Eero Saksman

Solmu 1/2000-2001
2000-08-29