Pythagoraan lause

Pythagoras Samoslainen

Pythagoras on legendaarinen kreikkalainen matematiikko ja filosofi. Tiedot hänen elämästään ovat epävarmoja ja ristiriitaisia. Tärkein Pythagorasta ja pythagoralaisia koskeva lähde on Lamblichosin (n. 300 eKr.) kirjoittama "Pythagoraan elämä". Suoria asiakirjoja ei ole säilynyt vaikka antiikissa kirjoitettiin useita Pythagoraan elämäkertoja. Seuraava kuvaus on peräisin E. S. Loomisilta, joka vuonna 1940 kokosi yhteen 370 todistusta Pythagoraan lauseesta.

Pythagoras syntyi Tyroksessa 569 eKr., mutta kasvoi Samoksella. Vuonna 549 hän matkusti Miletokseen, jossa han tapasi Thaleen ja Anaksimandroksen, joista ensimmäinen oli tuolloin 75-vuotias. Miletoksessa Pythagoras opiskeli kosmografiaa, joka tarkoitti fysiikkaa ja matematiikkaa. Pari vuotta myöhemmin hän matkusti Egyptiin, jossa hänesta tuli Theban uskonnollisen seuran jäsen. Kun persialaiset vuonna 526 valloittivat Egyptin, Pythagoras matkusti edelleen Babyloniaan, jossa hän tapasi intialaisia, kiinalaisia ja juutalaisia. Kymmenisen vuotta myöhemmin hän palasi Samokselle.

Kun Pythagoras vuonna 510 joutui tyranni Polykrateen epäsuosioon Samoksella, hän lähti Krotoniin Magna Graeciassa. Siellä hän piti puheita nuorille ja perusti koulun. Hän saikin melko pian suuren joukon oppilaita, joiden kanssa hän keskusteli etiikasta, sielun kuolemattomuudesta ja transmigraatiosta eli sielunvaelluksesta. Vuonna 490 Pythagoras jätti Krotonin ja muutti Tarasiin. Hän kuoli 99-vuotiaana vuonna 469 eKr. Metapontionissa. Prokloksen mukaan Pythagoras ja Thales toivat matematiikan idästa Kreikkaan. [TM93, s. 321]

Pythagoraan lause

Tämä matematiikan kuuluisin ja tunnetuin lause sanoo:

Suorakulmaisen kolmion hypotenuusan neliö on kateettien neliöiden summa, eli kuvan 1 merkinnöin c²=a²+b².

Kuva 1.

Pythagoraan lausetta havainnollistavia palapelejä
ja niihin liittyviä todistuksia

Palapeli 1

[Väi64, s. 48] Kuvassa 2 neliön sivun pituus on a + b kuten myös kuvassa 3, joten molemmat neliöt ovat samankokoisia. Molempiin neliöhin on sijoitettu neljä suorakulmaista kolmiota, joiden kateetit ovat a ja b, hypotenuusa c ja terävät kulmat $\alpha$ ja $\beta$ . Kolmioiden ulkopuoliset alueet ovat siis yhtäsuuret. Kuvan 2 nelikulmion sivut ovat kaikki yhtä pitkiä. Jokainen kulma on $180^\circ - (\alpha+\beta) = 180^\circ- 90^\circ = 90^\circ$ . Nelikulmio on siis neliö ja sen ala on c². Kuvassa 3 yhteneviä kolmioita on siirrelty siten, että muotostuu kaksi neliötä, joiden pinta-alat ovat a² ja b². Siispä c² = a² + b².

Kuva 2.

Kuva 3.

Bhaskaran todistus

Intialainen matemaatikko Bhaskara, joka eli 1150-luvulla, todisti Pythagoraan lauseen näin:

Kuva 4.

Neliön ala kuvassa 4 on kolmion hypotenuusan neliö. Se on jaettu neljäksi suorakulmaiseksi kolmioksi, joista jokainen on identtinen annetun kanssa, sekä pienemmäksi neliöksi [TM93, s. 320]. Pienen neliön sivun pituus x on kateettien erotus b-a.

Kuva 5.

Kuvassa 5 on palaset siirretty seuraavasti. Siinä on neljä yhtenevää kolmiota ja pieni neliö. Kuten aiemmin totesimme, on pienen neliön sivu sama kuin kateettien erotus.

Kuva 6.

Kuvassa 6 muodostuu kaksi neliötä kateettien sivuista. Todistus perustuu nyt siihen, etta kateettien muodostamat neliöt peittävät saman pinta-alan kuin kuvan 4 neliö, joten kateettien neliöiden summa on hypotenuusan neliö.

Kiinalainen todistus

Kiinalainen todistus, joka on peräisin teoksesta "Aritmeettinen klassikko gnomoneista ja taivaiden ympyräradoista", on seuraava.

Annettu suorakulmainen kolmio on kuvan 7 oikeassa yläkulmassa. Kolmio on peilattu hypotenuusan suhteen, ja näistä on otetut kolme kopiota on sijoitettu neliön muotoon. Keskelle jää pieni neliö, jonka sivun pituus on suorakulmaisten kolmioiden kateettien erotus. Näin ollen

$\begin{displaymath}c^2=4 \left( \frac{ab}{2}\right) + (a-b)^2 = 2ab + a^2 - 2ab +b^2 = a^2 + b^2 \qquad \cite[{\rm s}. 320]{Thomps:1993}. \end{displaymath}$

Kuva 7.

Palapeli 2

[TM93, s. 319] Yksi kaunis tapa hahmotella todistus on kuvassa 8:

Kuva 8.

Lyhyemmän kateetin neliö sekä neljä palapelin palaa, joista pitemmän kateetin neliö muodostetaan, voidaan siirtää niin, että ne täyttävät hypotenuusan neliön.

Jaetaan sivua b vasten piirretyn neliön sivut osiin, joiden pituudet ovat (b+a)/2 ja (b-a)/2. Yhdistetään jakopisteet janoilla AC ja BD. Nelikulmio EFBD on suunnikas, koska ED || FB ja |ED| = a+(b-a)/2 = (a+b)/2 = |BF|. Siis |DB| = c. Neliön symmetrian vuoksi myös |AC| = c. Erotetaan hypotenuusaa vasten piirretystä neliöstä kateetille b piirretyn neliön palojen kanssa yhtenevät palat. Voidaan ajatella, että palat siirretään kuvan osoittamalla tavalla. Keskelle muodostuu nelikulmio, jonka sivut ovat (b+a)/2 - (b-a)/2 = a ja jonka kaikki kulmat ovat symmetrian perusteella suoria; kyseessä on siis neliö. Laskemalla palasten alat saadaan c² = a² + b².

Muita Pythagoraan lauseen todistuksia

Thabit Ibn Quarran todistus

Thabit Ibn Quarran (n. 880) todistus on yksi kauneimmista [TM93, s. 318-319].

Kuva 9.

Olkoon ABC on annettu suorakulmainen kolmio. Piirretään kolmion ABC kanssa yhtenevä kolmio BDE kuvan 9 osoittamalla tavalla. Piirretään neliöt DEFG ja ACHG, joiden sivuina ovat yhtäpitkät kateetit DE ja AB sekä AC ja BD. Kulma $\angle CBE$ on suora.

Kuva 10.

Todistus perustuu nyt siihen, että kolmiota ABCkierretään $90^\circ$ vastapäivään pisteen Cympäri ja kolmiota DEB vastaavasti $90^\circ$ myötäpäivään pisteen E ympäri kuten kuvassa 10. Kolmio ABC saa tällöin paikan HB'C, kun taas kolmio DEB saa paikan FEB'. Neliön BCB'E ala on hypotenuusan |BC| = |BE| neliö. Siirtojen jälkeen tämä neliö on summa kahden kateetin neliöstä. Huomaa, että monikulmion CBEFH ala on sama molemmissa kuvissa.

Eukleideen todistus

Eukleideen todistus (lause 47 Elementan kirjassa 1.) perustuu kuvaan 11 [DI78, s. 113]:

Kuva 11.

Neliön FBAG ala on kaksi kertaa kolmion FBC ala (niillä on sama kanta ja korkeus). Suorakulmion BMLD ala on kaksi kertaa kolmion BAD ala (sama kanta ja korkeus). Osoitetaan, että $\triangle FBC \cong \triangle DAB$

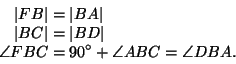
$\begin{displaymath}\begin{split} \vert FB\vert &= \vert BA\vert \\ \vert BC\ver... ...\\ \angle FBC &= 90^\circ+\angle ABC = \angle DBA. \end{split}\end{displaymath}$

Kolmiot ovat siis yhtenevat (sks).

On osoitettu: neliön FBAG alan puolikas on yhtä suuri kuin suorakulmion BDLM alan puolikas. Neliön FBAG ala on siis yhtä suuri kuin suorakulmion BDLM ala. Vastaavasti voidaan osoittaa, että neliön ACKH ala on yhtä suuri kuin suorakulmion MCNL ala.

Merkitään:

neliön FBAG sivu on a
neliön ACKH sivu on b
neliön BDNC sivu on c

On osoitettu, että a²+ b² on suorakulmioiden BMLD ja MLNC alojen summa eli c². Siis a²+ b²= c².

Sama todistus on Väisälän kirjassa "Keskikoulun geometria" [Väi64, s. 47-48].

Nimetön todistus

Mielestäni hienoin todistus Pythagoraan lauseelle on seuraava. Se perustuu kahteen periaatteseen:

(1) Pinta-alayksikkö on pituusyksikön neliö.
(2) Jos voidaan löytää kolme yhdenmuotoista kuviota, jotka voidaan piirtää kolmion sivuille siten, että kateeteilla a ja bolevien kuvioiden alojen summa $\Gamma+\Delta$ on yhtä kuin hypotenuusalla c olevan kuvion $\Sigma$ ala todistus on selvä. Oletetaan nimittäin, että pätee $\Sigma = \Gamma + \Delta$ . Tälloin seuraa (1):stä, että c²=a²+b².

Kuva 12.

Mutta jo kuvassa 12 oleva yksinkertainen konstruktio antaa yhden mahdollisuuden [TM93, s. 320]. Se sisältää vaaditut yhdenmuotoiset kolmiot ADC, CDB ja ACB.

Kolmiot ADC, CDB ja ABC ovat yhdenmuotoisia:

Jokaisessa on suorakulma
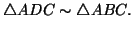
Kulma $\angle DAC = \alpha$ on molemmissa kolmioissa ADC ja ABC. Siis $\triangle ADC \sim \triangle ABC.$
Kulma $\angle DBC =\beta$ on molemmissa kolmioissa DBCja ABC. Siis $\triangle DBC \sim \triangle ABC$ .
Siis $\triangle DBC \sim \triangle ABC \sim \triangle ADC$ .
$\triangle ADC$ on piirretty sivulle AC
$\triangle DBC$ on piirretty sivulle BC
$\triangle ABC$ on piirretty sivulle AB

Olkoon A₁ kolmion $\triangle ADC$ ala, A₂ on kolmion $\triangle DBC$ ala ja A₃ kolmion $\triangle ABC$ ala.

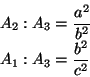
$\begin{displaymath}\begin{split} A_2 : A_3 &= \frac{a^2}{b^2} \\ A_1 : A_3 &= \frac{b^2}{c^2} \end{split}\end{displaymath}$

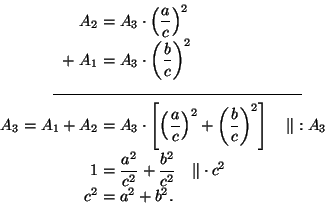
$\begin{displaymath}\begin{split} A_{2}&=A_{3}\cdot\left(\frac{a}{c}\right)^{2} \... ...}{c^2}\quad \Vert \cdot c^{2} \\ c^2 &= a^2 + b^2. \end{split}\end{displaymath}$

Viitteet

DI78

P. Dedron and J. Itard.
Mathematics and mathematicians 2.
The Open University Press., Stony Stratford, 2nd edition, 1978.

TM93

Jan Thompson and Thomas Martins.
Matematiikan käsikirja, käännös Soft Artist Oy.
WSOY, Juva, Tampere, 1993.

Väi64

Väisälä.
Keskikoulun geometria, kolmas painos.
Werner-Söderström OY, Porvoo-Helsinki, 3. painos, 1964.

Janis Künnap
Maunulan yhteiskoulu ja Helsingin matematiikkalukio

Solmu 1/2000-2001
2000-08-29