Geometriakulma 10: Mikä on pinta?

Kahdeksas geometriakulma pyrki määrittelemään käyrän. Pintoja voidaan käsitellä samaan tapaan.

Melko luontevalta -- ainakin liikaa pohtimatta -- tuntuu kutsua pinnaksi kahden muuttujan funktion f(x,y) kuvaajaa, so. niiden pisteiden (x,y,z) joukkoa, jotka toteuttavat yhtälön z = f(x,y). Tässähän xy"-tason pisteen (x,y) yläpuolelle (tai ala-) korkeuteen f(x,y) asetetaan yksi pinnan piste. Jos funktio f on jatkuva, pisteet ilmeisestikin sijaitsevat siten, että niiden voidaan kuvitella muodostavan pinnan. Tilanne on verrattavissa muodossa y = f(x) annettuun käyrään.

Selvyyden vuoksi todettakoon, että lukujen x, y ja z ajatellaan tällöin olevan suorakulmaisia koordinaatteja. Välttämätöntähän tämä ei ole. (Pallokoordinaatteja tunteva lukija pohtikoon, mitä edellä sanotusta tulisi, jos kyseessä olisivatkin pallokoordinaatit $z = r = \text{etäisyys origosta}$ , $x = \vartheta = \text{maantieteellinen leveys}$ , $y = \varphi = \text{maantieteellinen pituus}$ .)

Yksinkertaisena esimerkkinä olkoon suorakulmaisissa koordinaateissa annettu pinta

$\begin{displaymath}z = \frac{xy}{x^2 + y^2}, \end{displaymath}$

joka on määritelty kaikkialla muualla paitsi origossa. Oheinen kuvio osoittaa, että origon kohdalla pinta käyttäytyy hieman erikoisella tavalla. Funktiosta ei saada origossa jatkuvaa, annetaanpa sille origossa mikä tahansa arvo. Lukija miettiköön, onko hän valmis kutsumaan funktion kuvaajaa pinnaksi. (Määritelmäthän ovat tietyssä määrin mielivaltaisia: ne asetetaan täsmällistämään jokin intuitiivinen idea.) Kuvio on samalla esimerkki siitä, että funktion epäjatkuvuus voi olla monimutkaisempaa, kuin yhden muuttujan funktioiden antaman mielikuvan pohjalta voi kuvitella.

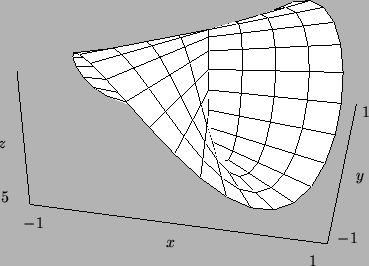
$\begin{picture}(100,100)(0,0) \put(0,0){\includegraphics[height=70mm, bbllx=0pt,... ...$1$ } \put(-3,45){$z$ } \put(-10,28){$-0.5$ } \put(-10,65){$0.5$ } \end{picture}$

Toisaalta muotoa F(x,y,z) = 0 oleva yhtälö tuntuisi ainakin aika usein esittävän pintaa. Esimerkiksi x² + y² + z² - R² = 0esittää R"=säteistä origokeskistä palloa. Muodossa z = f(x,y)esitetty pinta on tämän esitystavan erikoistapaus: z - f(x,y) = 0. Toisaalta mikä tahansa kolmen muuttujan funktio F ei kelpaa määrittelemään pintaa: x² + y² + z² + 1 = 0 ei esitä mitään; x² + y² + z² = 0 on yksi ainoa piste; (x - y)² + (y - z)² = 0 toteutuu vain, kun x = y = z, ts. kyseessä on origon kautta kulkeva suora.

Helpoin ja monikäyttöisin tapa pinnan esittämiseen on kuitenkin sen parametriesitys: Olkoon annettuna funktiot x(u,v), y(u,v)ja z(u,v). Kun parametrit u ja v saavat kaikki parametrialueen arvot, so. piste (u,v) sijaitsee eräässä uv"=tason joukossa, määrittävät funktiot xyz"=avaruuden pisteen (x(u,v),y(u,v),z(u,v)). Tämä on pinnan piste.

Funktioilta x, y ja z on edellytettävä jonkinlaista säännöllisyyttä, jotta syntyvää pistejoukkoa olisi järkevää kutsua pinnaksi. Jatkuvia niiden tulee ainakin olla. Tämä ei kuitenkaan riitä: jos esimerkiksi $x(u,v) = y(u,v) = z(u,v) = u + v^2 + \sin(uv)$ , on aina x = y = z, ja pisteet sijaitsevat suoralla. Mitä funktioista itse asiassa on oletettava, ei ole aivan yksinkertaista eikä täysin vakiintunutta matemaattisessa kirjallisuudessakaan. Lisätietoja kaipaava lukija etsiköön käsiinsä jonkin (hyvän) usean muuttujan analyysia käsittelevän oppikirjan.

Muodossa z = f(x,y) annetulle pinnalle on parametriesitys helposti kirjoitettavissa: parametreiksi valitaan u = x ja v = y, jolloin tarvittavat kolme funktiota ovat x(u,v) = u, y(u,v) = v, z(u,v) = f(u,v).

Parametriesityksen etsiminen pallopinnalle x² + y² + z² = R² ei ole aivan yhtä suoraviivaista. Mahdollisuuksiakin on useita. Pallokoordinaattien perusteella saataisiin

$\begin{displaymath}x = R\cos\vartheta\cos\varphi,\quad y = R\cos\vartheta\sin\varphi, \quad z = R\sin\vartheta, \end{displaymath}$

missä parametrialueena on $-\pi/2 \le \vartheta \le \pi/2$ , $-\pi \le \varphi \le \pi$ . Lausekkeet tulevat ymmärrettäviksi pohtimalla niitä alkeistrigonometrian ja oheisen kuvion valossa. Lukija voi myös laskemalla todeta, että lausekkeiden neliösumma todellakin on R².

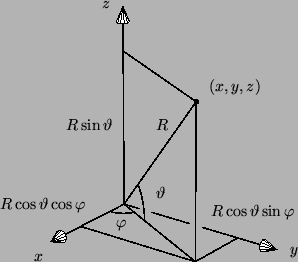
$\begin{picture}(200,120)(0,0) \put (37,-2){\includegraphics[height=60mm, bbllx=7... ...cos{\vartheta} \sin{\varphi}$ } \put (54,60){$R \sin{\vartheta}$ } \end{picture}$

Tällä pallon parametriesityksellä on heikkoutensa: Pallo tavallaan saadaan taivuttelemalla parametritason suorakulmio $\{(\vartheta,\varphi) \mid -\pi/2 \le \vartheta \le \pi/2,\ -\pi \le \varphi \le \pi\}$ pallopinnaksi ja liimaamalla reunat $\varphi = -\pi$ ja $\varphi = \pi$ yhteen; liimauskohta on pallon meridiaanikäyrä. Liimauskohdan eri puolilla sijaitsevat pallopinnan pisteet voivat olla hyvinkin lähellä toisiaan, mutta niitä vastaavat parametritason pisteet $(\vartheta,\varphi)$ ovat toisistaan kaukana.

Lukija miettikööön myös, mitkä pallopinnan pisteet syntyvät parametritason suorakulmion kahdesta muusta sivusta $\vartheta = -\pi/2$ , $\vartheta = \pi/2$ .

Hieman yksinkertaisempi esimerkki on ruuvipinta:

$\begin{displaymath}x = u \cos v, \quad y = u \sin v, \quad z = \frac{v}{2\pi}, \qquad 0 \le u \le 1, \quad 0 \le v \le 4\pi. \end{displaymath}$

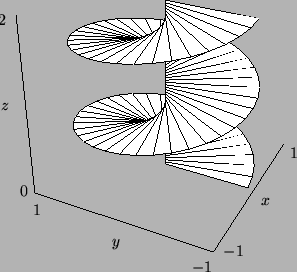
$\begin{picture}(100,100)(0,0) \put(0,0){\includegraphics[height=70mm, bbllx=0pt,... ...t(8,25){$1$ } \put(-2,58){$z$ } \put(4,31){$0$ } \put(-3,85){$2$ } \end{picture}$

Lopuksi harjoitustehtävä: Millainen on pinta

$\begin{displaymath}x = (v^2 - 1) \cos u, \quad y = (v^2 - 1) \sin u, \quad z = v\ ? \end{displaymath}$

Lukija miettiköön asiaa ensin pelkästään yhtälöitä pohtimalla. Jos käytetävissä on jokin sopiva tietokoneohjelma, pinnan voi piirtää. Tätä varten on kuitenkin ensin löydettävä sopiva parametrialue. Onko pinnalla joitakin erikoisasemassa olevia pisteitä?

P.S. Kuvat ovat peräisin laatimistani oppimateriaaleista: pinnat monisteesta Vektorimuuttujan analyysi, Otatieto 1999, ja pallokoordinaatit kirjasta M niinkuin matematiikka, MFKA 1998. Jälkimmäinen on saatavissa myös verkkodokumenttina.

Simo K. Kivelä

Solmu 1/2000-2001
2000-08-29